Fórmula de la tangente inversa

En trigonometría, los ángulos se evalúan con respecto a las funciones trigonométricas básicas de trigonometría que son seno, coseno, tangente, cotangente, secante y cosecante. Estas funciones trigonométricas tienen sus propias relaciones trigonométricas bajo diferentes ángulos que se utilizan en operaciones trigonométricas. Estas funciones también tienen sus inversas que se conocen como arcsin, arccos, arctan, arccot, arcsec y arccosec.

El artículo dado es el estudio de la tangente inversa o arctan. Incluye la explicación y derivación de una tangente inversa, fórmula de tangente inversa para la evaluación de ángulos y algunos problemas de muestra.

¿Qué es la tangente inversa?

La tangente inversa es una función de trigonometría que es inversa de la función trigonométrica tangente. También se conoce como arctan ya que el prefijo ‘-arc’ significa inverso en trigonometría. La tangente inversa se denota por tan ^-1 x.

La función de tangente inversa se utiliza para determinar el valor del ángulo por la relación de (perpendicular/base).

Considere un ángulo θ y la tangente del ángulo es igual a x. Entonces, dará la función inversa de la tangente.

Como, x = tanθ 

=> θ = bronceado ^-1 x

Matemáticamente, la tangente inversa se deriva de la relación entre la perpendicular y la base.

Consideremos un triángulo rectángulo PQR.

En el triángulo rectángulo, la función tangente PQR será 

=>tan θ = perpendicular/base

θ = tan ^-1 (p/b)

Fórmula de la tangente inversa

Como la tangente es una función trigonométrica similarmente, la tangente inversa es una función trigonométrica inversa de la tangente. Los valores de estas funciones inversas se derivan de la fórmula de la tangente inversa correspondiente, que puede expresarse en grados o radianes.

La lista de algunas de las fórmulas de la tangente inversa se dan a continuación:

• θ = arctan(perpendicular/base)
• arctan(-x) = -arctan(x) para todo x∈ R
• tan(arctan x) = x, para todos los números reales
• arctan(1/x) = π/2 – arctan(x) = arccot(x); si x>0

(O)

• arctan(1/x) = -π/2 – arctan(x) = arccot(x) -π ; si x<0
• sin(arctano x) = x/ √(1+x2)
• cos(arcano x) = 1/ √(1+x2)
• arctan(x) = 
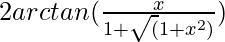
• arctan(x) = 

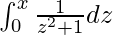
En trigonometría, también hay un conjunto separado de fórmulas de la tangente inversa con respecto a π.

• π/4 = 4 arctan(1/5) – arctan(1/239)
• π/4 = arctan(1/2) + arctan(1/3)
• π/4 = 2 arctan(1/2) – arctan(1/7)
• π/4 = 2 arctan(1/3) + arctan(1/7)
• π/4 = 8 arctan(1/10) – 4 arctan(1/515) – arctan(1/239)
• π/4 = 3 arctan(1/4) + arctan(1/20) + arctan(1/1985)

Tabla resumida de la tangente inversa

Hay algunos valores estándar establecidos para la tangente inversa en grados y radianes. Estos valores son fijos o derivados para hacer que la evaluación de los ángulos sea aún más conveniente bajo la función dada. Por lo tanto, la tabla a continuación proporciona estos valores de tangente inversa en grados y radianes.

X	Bronceado -1 (x) La licenciatura	Bronceado -1 (x) Radián
-∞	-90°	-π/2
-3	-71.565°	-1.2490
-2	-63.435°	-1.1071
-√3	-60°	-π/3
-1	-45°	-π/4
-1/√3	-30°	-π/6
-1/2	-26.565°	-0.4636
0	0°	0
1/2	26.565°	0.4636
1/√3	30°	π/6
1	45°	π/4
√3	60°	π/3
2	63.435°	1.1071
3	71.565°	1.2490
∞	90°	π/2

Problemas de muestra

Problema 1. Evaluar tan ^-1 (0.577).

Solución:

El valor de 0,577 es igual a tan30°.

=>0.577=bronceado(30°)

Después,

=>bronceado ^-1 (0.577)=bronceado ^-1 (30°)

=>30°

Problema 2. ¿Cuál es el inverso de tan60°?

Solución:

El valor de tan60° es igual a 1,732.

=>bronceado60°=1.732

Después,

bronceado ^-1 (60°)= bronceado ^-1 (1.732)

=>1.732

Problema 3. ¿Cuál es el inverso de tan45°?

Solución:

El valor de tan45° es igual a 1.

=>bronceado45°=1

Después,

bronceado ^-1 (45°)=bronceado ^-1 (1)

=>1

Problema 4. ¿Cuál es el inverso de tan30°?

Solución:

El valor de tan30° es igual a 0,577

=>bronceado60°=0.577

Después,

tan-1(30°)=tan-1(0.577)

=>0.577

Problema 5. ¿Cuál es el inverso de tan90°?

Solución:

El valor de tan90° es igual a 0.

=>bronceado60°=1.732

Después,

bronceado ^-1 (90°)=bronceado ^-1 (0)

=>0