ML | Distancia entre clústeres e intracluster

Análisis de conglomerados:
el objetivo del proceso de conglomerado es descubrir patrones generales de distribución y correlaciones interesantes entre los atributos de los datos. Es la tarea de agrupar un conjunto de objetos de tal manera que los objetos de un mismo grupo sean más parecidos entre sí que con los de otros grupos. El análisis de conglomerados en sí mismo no es un algoritmo específico, sino la tarea general a resolver. Se puede lograr mediante varios algoritmos que difieren significativamente en su comprensión de lo que constituye un grupo y cómo encontrarlos de manera eficiente. Las nociones populares de conglomerados incluyen grupos con pequeñas distancias entre los miembros del conglomerado, áreas densas del espacio de datos, intervalos o distribuciones estadísticas particulares.

Aquí, discutiremos sobre la distancia entre los objetos de los diferentes grupos y los objetos de los mismos grupos. Tenemos dos tipos de distancia: distancia entre grupos y distancia entre grupos .

Sean S y T grupos formados usando la partición U. d(x, y)es la distancia entre dos objetos xey pertenecientes a S y T respectivamente. d(x, y)se calcula utilizando métodos de cálculo de distancia bien conocidos como Euclidean, Manhattan y Chebychev. |S| y |T| son el número de objetos en los grupos S y T respectivamente.

Distancia entre ejes:

La distancia entre grupos es la distancia entre dos objetos que pertenecen a dos grupos diferentes. Es de 5 tipos –

Distancia de enlace único: la distancia de enlace único es la distancia más cercana entre dos objetos que pertenecen a dos grupos diferentes definidos como:
$\delta_{1}(S, T)=\min \left\{\begin{array}{c} d(x, y) \\ x \in S, y \in T \end{array}\right\}$
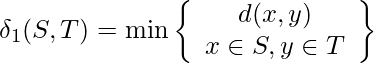
Distancia de enlace completa: La distancia de enlace completa es la distancia entre los dos objetos más remotos que pertenecen a dos grupos diferentes definidos como:
$\delta_{2}(S, T)=\max \left\{\begin{array}{c} d(x, y) \\ x \in S, y \in T \end{array}\right\}$
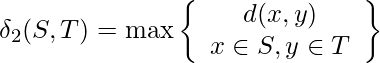
Distancia de vinculación promedio: la distancia de vinculación promedio es la distancia promedio entre todos los objetos que pertenecen a dos grupos diferentes definidos como:
$\delta_{3}(S, T)=\frac{1}{|S||T|} \sum_{x \in S \atop y \in T} d(x, y)$
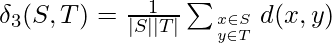
Distancia de enlace del centroide: La distancia de enlace del centroide es la distancia entre los centros vs y vt de dos grupos S y T respectivamente, definida como:
$\delta_{4}(S, T)=d\left(\mathcal{v}_{s}, v_{t}\right)$
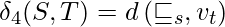
dónde,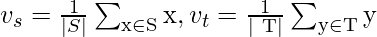
$v_{s}=\frac{1}{|S|} \sum_{\mathrm{x} \in \mathrm{S}} \mathrm{x}, v_{t}=\frac{1}{|\mathrm{~T}|} \sum_{\mathrm{y} \in \mathrm{T}} \mathrm{y}$
Distancia media de enlace centroide: La distancia media de enlace centroide es la distancia entre el centro de un grupo y todos los objetos que pertenecen a un grupo diferente, definida como:
$\delta_{5}(\mathrm{~S}, \mathrm{~T})=\frac{1}{|\mathrm{~S}|+|\mathrm{T}|}\left\{\sum_{\mathrm{x} \in \mathrm{S}} \mathrm{d}(\mathrm{x}, \mathrm{vt})+\sum_{\mathrm{y} \in \mathrm{T}} \mathrm{d}(\mathrm{y}, \mathrm{vs})\right\}$

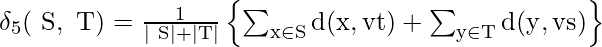
Distancia intracubridor:

La distancia intracluster es la distancia entre dos objetos pertenecientes al mismo cluster. Es de 3 tipos –

Distancia de diámetro completo: la distancia de diámetro completo es la distancia entre dos objetos más remotos que pertenecen al mismo grupo definido como:
$\Delta_{1}(S)=\max \{d(x, y)\}$
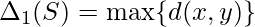
Distancia de diámetro promedio: la distancia de diámetro promedio es la distancia promedio entre todos los objetos que pertenecen al mismo grupo definido como:
$\Delta_{2}(S)=\frac{1}{|S| \cdot(|S|-1)} \sum_{x, y \atop x \neq y}\{d(x, y)\}$
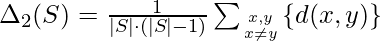
Distancia del diámetro del centroide: la distancia del diámetro del centroide es el doble de la distancia promedio entre todos los objetos y el centro del grupo de s definido como:
$\Delta_{3}(S)=2\left\{\frac{\sum_{x \in S} d(x, \bar{v})}{|S|}\right\}$
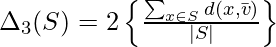
dónde,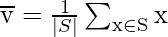
$\overline{\mathrm{v}}=\frac{1}{|S|} \sum_{\mathrm{x} \in \mathrm{S}} \mathrm{x}$

Nota:
si un algoritmo de agrupamiento crea agrupaciones de modo que la distancia entre agrupaciones entre diferentes agrupaciones sea mayor y la distancia dentro de las agrupaciones del mismo agrupamiento sea menor, entonces podemos decir que es un buen algoritmo de agrupamiento.

Aquí algoritmo de agrupamiento en
Fig. 3
es mejor que
Figura 2
y
Figura 1
como en
Fig. 3
La distancia entre grupos es mayor y la distancia entre grupos es menor.

Referencia: https://en.wikipedia.org/wiki/Hierarchical_clustering

Publicación traducida automáticamente

Artículo escrito por soumya7 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Distancia entre ejes:

Distancia intracubridor:

Deja una respuesta Cancelar la respuesta