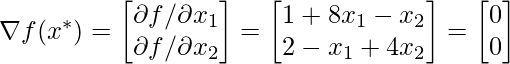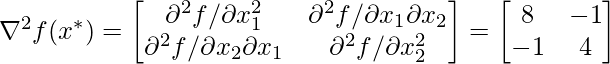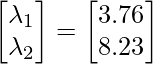Wikipedia define la optimización como un problema en el que maximizas o minimizas una función real eligiendo sistemáticamente valores de entrada de un conjunto permitido y calculando el valor de la función. Eso significa que cuando hablamos de optimización siempre estamos interesados en encontrar la mejor solución. Entonces, digamos que uno tiene alguna forma funcional (por ejemplo, en la forma de f(x)) y está tratando de encontrar la mejor solución para esta forma funcional. Ahora bien, ¿qué significa mejor? Uno podría decir que está interesado en minimizar esta forma funcional o maximizar esta forma funcional.
Generalmente, un problema de optimización tiene tres componentes.
minimizar f(x),
wrt x ,
sujeto a a < x < b
donde, f(x) : Función objetivo
x : Variable de decisión
a < x < b : Restricción
¿Qué es un problema de optimización multivariante?
En un problema de optimización multivariante, existen múltiples variables que actúan como variables de decisión en el problema de optimización.
z = f(x 1 ,x 2 ,x 3 …..x n )
Entonces, cuando observa este tipo de problemas, una función general z podría ser una función no lineal de las variables de decisión x 1 ,x 2 ,x 3 a x n . Entonces, hay n variables que uno podría manipular o elegir para optimizar esta función z. Tenga en cuenta que uno podría explicar la optimización univariante usando imágenes en dos dimensiones porque en la dirección x teníamos el valor de la variable de decisión y en la dirección y teníamos el valor de la función. Sin embargo, si se trata de optimización multivariante, entonces tenemos que usar imágenes en tres dimensiones y si las variables de decisión son más de 2, entonces es difícil de visualizar.
¿Qué es la optimización multivariante sin restricciones?
Como su nombre indica, la optimización multivariante sin restricciones se conoce como optimización multivariante sin restricciones.
Ejemplo :
min f(x̄) con respecto a
x̄
x̄ ∈ R n
Entonces, cuando observa este problema de optimización, generalmente lo escribe en la forma anterior donde dice que va a minimizar f (x̄), y esta función se llama función objetivo. Y la variable que puede usar para minimizar esta función, que se llama la variable de decisión, se escribe a continuación así: wrt x̄ aquí y también dice que x̄ es continua, es decir, podría tomar cualquier valor en la línea de números reales.
Las condiciones necesarias y suficientes para que x̄ * sea el minimizador de la función f(x̄ * )
En caso de optimización multivariada las condiciones necesarias y suficientes para que x̄ * sea el minimizador de la función f(x̄) son:
Condición necesaria de primer orden: ∇ f(x̄ * ) = 0
Condición de suficiencia de segundo orden: ∇ 2 f(x̄ * ) tiene que ser definida positiva.
dónde,
,y
Resolvamos rápidamente un ejemplo numérico sobre esto para comprender mejor estas condiciones.
Ejemplo numérico
Problem: minSolution: According to the first-order condition
By solving the two equation we got value of and
as
To check whether this is a maximum point or a minimum point, and to do so we look at the second-order sufficiency condition. So according to the second-order sufficiency condition: And we know that the Hessian matrix is said to be positive definite at a point if all the eigenvalues of the Hessian matrix are positive. So now let's find the eigenvalues of the above Hessian matrix. To find eigenvalue refer here. And to find eigenvalue in python refer here. So the eigenvalue of the above hessian matrix is So the eigenvalues for this found to be both positive; that means, that this is a minimum point.
Publicación traducida automáticamente
Artículo escrito por AmiyaRanjanRout y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA