Regla de Cramer : En álgebra lineal, la regla de Cramer es una fórmula explícita para la solución de un sistema de ecuaciones lineales con tantas ecuaciones como variables desconocidas. Expresa la solución en términos de los determinantes de la array de coeficientes y de las arrays obtenidas de ella reemplazando una columna por el vector columna de los lados derechos de las ecuaciones. La regla de Cramer es computacionalmente ineficiente para sistemas de más de dos o tres ecuaciones.
Supongamos que tenemos que resolver estas ecuaciones:
a 1 x + b 1 y + c 1 z = d 1
a 2 x + b 2 y + c 2 z = d 2
a 3 x + b 3y + c 3 z = d 3
Siguiendo la regla de Cramer , primero encuentre los valores determinantes de las cuatro arrays.
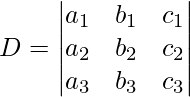[Tex]D_1 = \begin{vmatrix} d_1 & b_1 & c_1\\ d_2 & b_2 & c_2\\ d_3 & b_3 & c_3\\ \end{vmatrix} [/Tex]
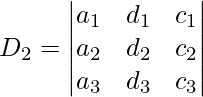[Tex]D_3 = \begin{vmatrix} a_1 & b_1 & d_1\\ a_2 & b_2 & d_2\\ a_3 & b_3 & d_3\\ \end{vmatrix} [/Tex]
Hay 2 casos:
Caso I : Cuando D ≠ 0 En este caso tenemos,
x = D1/D
y = D2/D
z = D3/D
Por lo tanto se obtendrá un valor único de x, y, z.
Caso II : Cuando D = 0
(a) Cuando al menos uno de D1, D2 y D3 no es cero : Entonces no hay solución posible y, por lo tanto, el sistema de ecuaciones será inconsistente.
(b) Cuando D = 0 y D1 = D2 = D3 = 0 : Entonces el sistema de ecuaciones será consistente y tendrá infinitas soluciones.
Ejemplo
Considere el siguiente sistema de ecuaciones lineales.
[2x – y + 3z = 9], [x + y + z = 6], [x – y + z = 2]
[Tex]D_1 = \begin{vmatrix} 9 & -1 & 3\\ 6 & 1 & 1\\ 2 & -1 & 1\\ \end{vmatrix} [/Tex]
[Tex]D_3 = \begin{ varray} 2 y -1 y 9\\ 1 y 1 y 6\\ 1 y -1 y 2\\ \end{varray} [/Tex]
[x = re 1 /D = 1], [y = re 2 /D = 2], [z = re 3 /D = 3]
A continuación se muestra la implementación.
C++
// CPP program to calculate solutions of linear
// equations using cramer's rule
#include <bits/stdc++.h>
using namespace std;
// This functions finds the determinant of Matrix
double determinantOfMatrix(double mat[3][3])
{
double ans;
ans = mat[0][0] * (mat[1][1] * mat[2][2] - mat[2][1] * mat[1][2])
- mat[0][1] * (mat[1][0] * mat[2][2] - mat[1][2] * mat[2][0])
+ mat[0][2] * (mat[1][0] * mat[2][1] - mat[1][1] * mat[2][0]);
return ans;
}
// This function finds the solution of system of
// linear equations using cramer's rule
void findSolution(double coeff[3][4])
{
// Matrix d using coeff as given in cramer's rule
double d[3][3] = {
{ coeff[0][0], coeff[0][1], coeff[0][2] },
{ coeff[1][0], coeff[1][1], coeff[1][2] },
{ coeff[2][0], coeff[2][1], coeff[2][2] },
};
// Matrix d1 using coeff as given in cramer's rule
double d1[3][3] = {
{ coeff[0][3], coeff[0][1], coeff[0][2] },
{ coeff[1][3], coeff[1][1], coeff[1][2] },
{ coeff[2][3], coeff[2][1], coeff[2][2] },
};
// Matrix d2 using coeff as given in cramer's rule
double d2[3][3] = {
{ coeff[0][0], coeff[0][3], coeff[0][2] },
{ coeff[1][0], coeff[1][3], coeff[1][2] },
{ coeff[2][0], coeff[2][3], coeff[2][2] },
};
// Matrix d3 using coeff as given in cramer's rule
double d3[3][3] = {
{ coeff[0][0], coeff[0][1], coeff[0][3] },
{ coeff[1][0], coeff[1][1], coeff[1][3] },
{ coeff[2][0], coeff[2][1], coeff[2][3] },
};
// Calculating Determinant of Matrices d, d1, d2, d3
double D = determinantOfMatrix(d);
double D1 = determinantOfMatrix(d1);
double D2 = determinantOfMatrix(d2);
double D3 = determinantOfMatrix(d3);
printf("D is : %lf \n", D);
printf("D1 is : %lf \n", D1);
printf("D2 is : %lf \n", D2);
printf("D3 is : %lf \n", D3);
// Case 1
if (D != 0) {
// Coeff have a unique solution. Apply Cramer's Rule
double x = D1 / D;
double y = D2 / D;
double z = D3 / D; // calculating z using cramer's rule
printf("Value of x is : %lf\n", x);
printf("Value of y is : %lf\n", y);
printf("Value of z is : %lf\n", z);
}
// Case 2
else {
if (D1 == 0 && D2 == 0 && D3 == 0)
printf("Infinite solutions\n");
else if (D1 != 0 || D2 != 0 || D3 != 0)
printf("No solutions\n");
}
}
// Driver Code
int main()
{
// storing coefficients of linear equations in coeff matrix
double coeff[3][4] = {
{ 2, -1, 3, 9 },
{ 1, 1, 1, 6 },
{ 1, -1, 1, 2 },
};
findSolution(coeff);
return 0;
}
Java
// Java program to calculate solutions of linear
// equations using cramer's rule
class GFG
{
// This functions finds the determinant of Matrix
static double determinantOfMatrix(double mat[][])
{
double ans;
ans = mat[0][0] * (mat[1][1] * mat[2][2] - mat[2][1] * mat[1][2])
- mat[0][1] * (mat[1][0] * mat[2][2] - mat[1][2] * mat[2][0])
+ mat[0][2] * (mat[1][0] * mat[2][1] - mat[1][1] * mat[2][0]);
return ans;
}
// This function finds the solution of system of
// linear equations using cramer's rule
static void findSolution(double coeff[][])
{
// Matrix d using coeff as given in cramer's rule
double d[][] = {
{ coeff[0][0], coeff[0][1], coeff[0][2] },
{ coeff[1][0], coeff[1][1], coeff[1][2] },
{ coeff[2][0], coeff[2][1], coeff[2][2] },
};
// Matrix d1 using coeff as given in cramer's rule
double d1[][] = {
{ coeff[0][3], coeff[0][1], coeff[0][2] },
{ coeff[1][3], coeff[1][1], coeff[1][2] },
{ coeff[2][3], coeff[2][1], coeff[2][2] },
};
// Matrix d2 using coeff as given in cramer's rule
double d2[][] = {
{ coeff[0][0], coeff[0][3], coeff[0][2] },
{ coeff[1][0], coeff[1][3], coeff[1][2] },
{ coeff[2][0], coeff[2][3], coeff[2][2] },
};
// Matrix d3 using coeff as given in cramer's rule
double d3[][] = {
{ coeff[0][0], coeff[0][1], coeff[0][3] },
{ coeff[1][0], coeff[1][1], coeff[1][3] },
{ coeff[2][0], coeff[2][1], coeff[2][3] },
};
// Calculating Determinant of Matrices d, d1, d2, d3
double D = determinantOfMatrix(d);
double D1 = determinantOfMatrix(d1);
double D2 = determinantOfMatrix(d2);
double D3 = determinantOfMatrix(d3);
System.out.printf("D is : %.6f \n", D);
System.out.printf("D1 is : %.6f \n", D1);
System.out.printf("D2 is : %.6f \n", D2);
System.out.printf("D3 is : %.6f \n", D3);
// Case 1
if (D != 0)
{
// Coeff have a unique solution. Apply Cramer's Rule
double x = D1 / D;
double y = D2 / D;
double z = D3 / D; // calculating z using cramer's rule
System.out.printf("Value of x is : %.6f\n", x);
System.out.printf("Value of y is : %.6f\n", y);
System.out.printf("Value of z is : %.6f\n", z);
}
// Case 2
else
{
if (D1 == 0 && D2 == 0 && D3 == 0)
System.out.printf("Infinite solutions\n");
else if (D1 != 0 || D2 != 0 || D3 != 0)
System.out.printf("No solutions\n");
}
}
// Driver Code
public static void main(String[] args)
{
// storing coefficients of linear
// equations in coeff matrix
double coeff[][] = {{ 2, -1, 3, 9 },
{ 1, 1, 1, 6 },
{ 1, -1, 1, 2 }};
findSolution(coeff);
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 program to calculate
# solutions of linear equations
# using cramer's rule
# This functions finds the
# determinant of Matrix
def determinantOfMatrix(mat):
ans = (mat[0][0] * (mat[1][1] * mat[2][2] -
mat[2][1] * mat[1][2]) -
mat[0][1] * (mat[1][0] * mat[2][2] -
mat[1][2] * mat[2][0]) +
mat[0][2] * (mat[1][0] * mat[2][1] -
mat[1][1] * mat[2][0]))
return ans
# This function finds the solution of system of
# linear equations using cramer's rule
def findSolution(coeff):
# Matrix d using coeff as given in
# cramer's rule
d = [[coeff[0][0], coeff[0][1], coeff[0][2]],
[coeff[1][0], coeff[1][1], coeff[1][2]],
[coeff[2][0], coeff[2][1], coeff[2][2]]]
# Matrix d1 using coeff as given in
# cramer's rule
d1 = [[coeff[0][3], coeff[0][1], coeff[0][2]],
[coeff[1][3], coeff[1][1], coeff[1][2]],
[coeff[2][3], coeff[2][1], coeff[2][2]]]
# Matrix d2 using coeff as given in
# cramer's rule
d2 = [[coeff[0][0], coeff[0][3], coeff[0][2]],
[coeff[1][0], coeff[1][3], coeff[1][2]],
[coeff[2][0], coeff[2][3], coeff[2][2]]]
# Matrix d3 using coeff as given in
# cramer's rule
d3 = [[coeff[0][0], coeff[0][1], coeff[0][3]],
[coeff[1][0], coeff[1][1], coeff[1][3]],
[coeff[2][0], coeff[2][1], coeff[2][3]]]
# Calculating Determinant of Matrices
# d, d1, d2, d3
D = determinantOfMatrix(d)
D1 = determinantOfMatrix(d1)
D2 = determinantOfMatrix(d2)
D3 = determinantOfMatrix(d3)
print("D is : ", D)
print("D1 is : ", D1)
print("D2 is : ", D2)
print("D3 is : ", D3)
# Case 1
if (D != 0):
# Coeff have a unique solution.
# Apply Cramer's Rule
x = D1 / D
y = D2 / D
# calculating z using cramer's rule
z = D3 / D
print("Value of x is : ", x)
print("Value of y is : ", y)
print("Value of z is : ", z)
# Case 2
else:
if (D1 == 0 and D2 == 0 and
D3 == 0):
print("Infinite solutions")
elif (D1 != 0 or D2 != 0 or
D3 != 0):
print("No solutions")
# Driver Code
if __name__ == "__main__":
# storing coefficients of linear
# equations in coeff matrix
coeff = [[2, -1, 3, 9],
[1, 1, 1, 6],
[1, -1, 1, 2]]
findSolution(coeff)
# This code is contributed by Chitranayal
C#
// C# program to calculate solutions of linear
// equations using cramer's rule
using System;
class GFG
{
// This functions finds the determinant of Matrix
static double determinantOfMatrix(double [,]mat)
{
double ans;
ans = mat[0,0] * (mat[1,1] * mat[2,2] - mat[2,1] * mat[1,2])
- mat[0,1] * (mat[1,0] * mat[2,2] - mat[1,2] * mat[2,0])
+ mat[0,2] * (mat[1,0] * mat[2,1] - mat[1,1] * mat[2,0]);
return ans;
}
// This function finds the solution of system of
// linear equations using cramer's rule
static void findSolution(double [,]coeff)
{
// Matrix d using coeff as given in cramer's rule
double [,]d = {
{ coeff[0,0], coeff[0,1], coeff[0,2] },
{ coeff[1,0], coeff[1,1], coeff[1,2] },
{ coeff[2,0], coeff[2,1], coeff[2,2] },
};
// Matrix d1 using coeff as given in cramer's rule
double [,]d1 = {
{ coeff[0,3], coeff[0,1], coeff[0,2] },
{ coeff[1,3], coeff[1,1], coeff[1,2] },
{ coeff[2,3], coeff[2,1], coeff[2,2] },
};
// Matrix d2 using coeff as given in cramer's rule
double [,]d2 = {
{ coeff[0,0], coeff[0,3], coeff[0,2] },
{ coeff[1,0], coeff[1,3], coeff[1,2] },
{ coeff[2,0], coeff[2,3], coeff[2,2] },
};
// Matrix d3 using coeff as given in cramer's rule
double [,]d3 = {
{ coeff[0,0], coeff[0,1], coeff[0,3] },
{ coeff[1,0], coeff[1,1], coeff[1,3] },
{ coeff[2,0], coeff[2,1], coeff[2,3] },
};
// Calculating Determinant of Matrices d, d1, d2, d3
double D = determinantOfMatrix(d);
double D1 = determinantOfMatrix(d1);
double D2 = determinantOfMatrix(d2);
double D3 = determinantOfMatrix(d3);
Console.Write("D is : {0:F6} \n", D);
Console.Write("D1 is : {0:F6} \n", D1);
Console.Write("D2 is : {0:F6} \n", D2);
Console.Write("D3 is : {0:F6} \n", D3);
// Case 1
if (D != 0)
{
// Coeff have a unique solution. Apply Cramer's Rule
double x = D1 / D;
double y = D2 / D;
double z = D3 / D; // calculating z using cramer's rule
Console.Write("Value of x is : {0:F6}\n", x);
Console.Write("Value of y is : {0:F6}\n", y);
Console.Write("Value of z is : {0:F6}\n", z);
}
// Case 2
else
{
if (D1 == 0 && D2 == 0 && D3 == 0)
Console.Write("Infinite solutions\n");
else if (D1 != 0 || D2 != 0 || D3 != 0)
Console.Write("No solutions\n");
}
}
// Driver Code
public static void Main()
{
// storing coefficients of linear
// equations in coeff matrix
double [,]coeff = {{ 2, -1, 3, 9 },
{ 1, 1, 1, 6 },
{ 1, -1, 1, 2 }};
findSolution(coeff);
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to calculate solutions of linear
// equations using cramer's rule
// This functions finds the determinant of Matrix
function determinantOfMatrix(mat)
{
let ans;
ans = mat[0][0] * (mat[1][1] * mat[2][2] - mat[2][1] * mat[1][2])
- mat[0][1] * (mat[1][0] * mat[2][2] - mat[1][2] * mat[2][0])
+ mat[0][2] * (mat[1][0] * mat[2][1] - mat[1][1] * mat[2][0]);
return ans;
}
// This function finds the solution of system of
// linear equations using cramer's rule
function findSolution(coeff)
{
// Matrix d using coeff as given in cramer's rule
let d = [[coeff[0][0], coeff[0][1], coeff[0][2]],
[coeff[1][0], coeff[1][1], coeff[1][2]],
[coeff[2][0], coeff[2][1], coeff[2][2]]];
// Matrix d1 using coeff as given in cramer's rule
let d1 = [[coeff[0][3], coeff[0][1], coeff[0][2]],
[coeff[1][3], coeff[1][1], coeff[1][2]],
[coeff[2][3], coeff[2][1], coeff[2][2]]];
// Matrix d2 using coeff as given in cramer's rule
let d2 = [[coeff[0][0], coeff[0][3], coeff[0][2]],
[coeff[1][0], coeff[1][3], coeff[1][2]],
[coeff[2][0], coeff[2][3], coeff[2][2]]];
// Matrix d3 using coeff as given in cramer's rule
let d3 = [[coeff[0][0], coeff[0][1], coeff[0][3]],
[coeff[1][0], coeff[1][1], coeff[1][3]],
[coeff[2][0], coeff[2][1], coeff[2][3]]];
// Calculating Determinant of Matrices d, d1, d2, d3
let D = determinantOfMatrix(d);
let D1 = determinantOfMatrix(d1);
let D2 = determinantOfMatrix(d2);
let D3 = determinantOfMatrix(d3);
document.write("D is : ", D.toFixed(6)+"<br>");
document.write("D1 is : ", D1.toFixed(6)+"<br>");
document.write("D2 is : ", D2.toFixed(6)+"<br>");
document.write("D3 is : ", D3.toFixed(6)+"<br>");
// Case 1
if (D != 0)
{
// Coeff have a unique solution. Apply Cramer's Rule
let x = D1 / D;
let y = D2 / D;
let z = D3 / D; // calculating z using cramer's rule
document.write("Value of x is : ", x.toFixed(6)+"<br>");
document.write("Value of y is : ", y.toFixed(6)+"<br>");
document.write("Value of z is : ", z.toFixed(6)+"<br>");
}
// Case 2
else
{
if (D1 == 0 && D2 == 0 && D3 == 0)
document.write("Infinite solutions\n");
else if (D1 != 0 || D2 != 0 || D3 != 0)
document.write("No solutions\n");
}
}
// Driver Code
let coeff = [[2, -1, 3, 9],
[1, 1, 1, 6],
[1, -1, 1, 2]]
findSolution(coeff);
// This code is contributed by avanitrachhadiya2155
</script>
Output: D is : -2.000000 D1 is : -2.000000 D2 is : -4.000000 D3 is : -6.000000 Value of x is : 1.000000 Value of y is : 2.000000 Value of z is : 3.000000
Publicación traducida automáticamente
Artículo escrito por bhonesh chawla y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA