Regresión lineal: es un tipo de análisis predictivo de uso común. Es un enfoque estadístico para modelar la relación entre una variable dependiente y un conjunto dado de variables independientes.
Hay dos tipos de regresión lineal.
- Regresión lineal simple
- Regresión lineal múltiple
Analicemos la regresión lineal simple usando R.
Regresión lineal simple:
Es un método estadístico que nos permite resumir y estudiar relaciones entre dos variables continuas (cuantitativas). Una variable denotada x se considera una variable independiente y la otra denotada y se considera una variable dependiente. Se supone que las dos variables están linealmente relacionadas. Por lo tanto, tratamos de encontrar una función lineal que prediga el valor de respuesta (y) con la mayor precisión posible como función de la característica o variable independiente (x).
Para comprender el concepto, consideremos un conjunto de datos de salarios donde se da el valor de la variable dependiente (salario) para cada variable independiente (años de experiencia).
Conjunto de datos de salarios:
Years experienced Salary
1.1 39343.00
1.3 46205.00
1.5 37731.00
2.0 43525.00
2.2 39891.00
2.9 56642.00
3.0 60150.00
3.2 54445.00
3.2 64445.00
3.7 57189.00
Para propósitos generales, definimos:
- x como un vector de características, es decir, x = [x_1, x_2, …., x_n],
- y como vector de respuesta, es decir, y = [y_1, y_2, …., y_n]
- para n observaciones (en el ejemplo anterior, n=10).
Gráfico de dispersión del conjunto de datos dado:
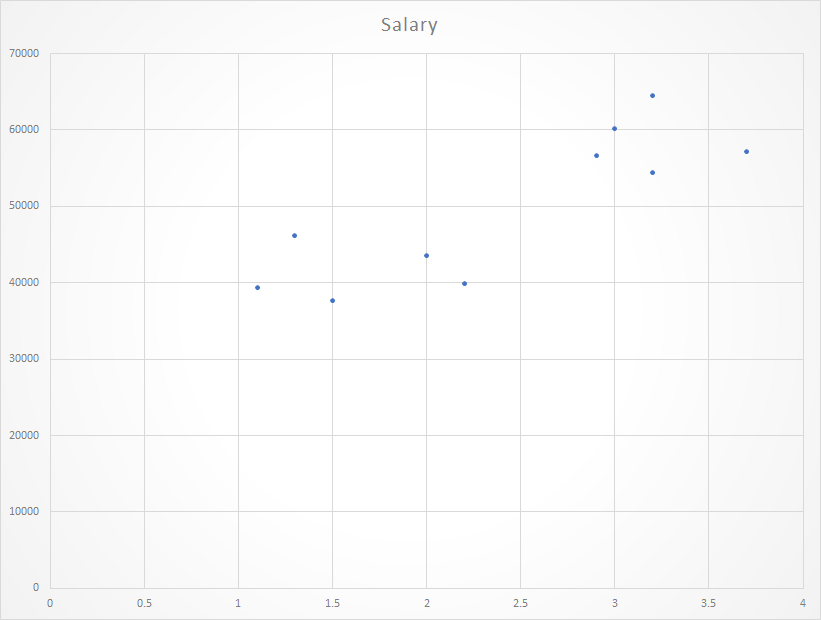
Ahora, tenemos que encontrar una línea que se ajuste al gráfico de dispersión anterior a través del cual podamos predecir cualquier valor de y o la respuesta para cualquier valor de x .
La línea que mejor se ajusta se llama la línea de regresión .
La ecuación de la recta de regresión está dada por:
y = a + bx
Donde y es el valor de respuesta pronosticado, a es la intersección con y, x es el valor de la característica y b es una pendiente.
Para crear el modelo, evalúemos los valores de los coeficientes de regresión a y b. Y tan pronto como se realiza la estimación de estos coeficientes, se puede predecir el modelo de respuesta. Aquí vamos a utilizar la técnica de mínimos cuadrados .
El principio de mínimos cuadrados es uno de los métodos populares para encontrar una curva que se ajuste a unos datos dados. Digamos (x1, y1), (x2, y2)….(xn, yn) sean n observaciones de un experimento. Estamos interesados en encontrar una curva que se ![]()
ajuste estrechamente a los datos dados de tamaño ‘n’. Ahora, en x=x1, mientras que el valor observado de y es y1, el valor esperado de y de la curva (1) es f(x1). Entonces el residual puede ser definido por… ![]()
De manera similar, los residuales para x2, x3…xn están dados por…![]()
![]()
![]()
Al evaluar el residual, encontraremos que algunos residuales son positivos y otros negativos. Esperamos encontrar la curva que se ajuste a los datos dados de modo que el residuo en cualquier xi sea mínimo. Dado que algunos de los residuos son positivos y otros son negativos y como nos gustaría dar la misma importancia a todos los residuos, es conveniente considerar la suma de los cuadrados de estos residuos. Así consideramos: ![]()
y encontramos la mejor curva representativa.
Ajuste por mínimos cuadrados de una línea recta
Supongamos, dado un conjunto de datos (x1, y1), (x2, y2), (x3, y3)…..(xn, yn) de n observación de un experimento. Y nos interesa ajustar una línea recta. ![]()
a los datos dados.
Ahora considere: ![]()
Ahora considere la suma de los cuadrados de ei ![Rendered by QuickLaTeX.com \begin{array}{c} E=\sum_{i=1}^{n} e_{i}^{2} \\ =\sum_{i=1}^{n}\left[y_{i}-\left(a x_{i}+b\right)\right]^{2} \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3bc10940ced22ef939ea83523ce9346_l3.png)
Nota: E es una función de los parámetros a y b y necesitamos encontrar a y b tales que E sea mínimo y la condición necesaria para que E sea mínimo es la siguiente:
![]()
This condition yields: ![Rendered by QuickLaTeX.com \begin{array}{l} \frac{\partial E}{\partial a}=\sum_{i=1}^{n} 2 x_{i}\left[y_{i}-\left(a x_{i}+b\right)\right]=0 \\ a \sum_{i=1}^{n} x_{i}+n b=\sum_{i=1}^{n} y_{i} \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32c0639753d92e22f59c8f57b5ae474e_l3.png)
The above two equations are called normal equations which are solved to get the value of a and b.
The Expression for E can be rewritten as: ![]()
The basic syntax for a regression analysis in R is
lm(Y ~ model)
donde Y es el objeto que contiene la variable dependiente a predecir y modelo es la fórmula del modelo matemático elegido.
El comando lm() proporciona los coeficientes del modelo pero no proporciona información estadística adicional.
El siguiente código R se usa para implementar la REGRESIÓN LINEAL SIMPLE :
Python3
# Simple Linear Regression
# Importing the dataset
dataset = read.csv('salary.csv')
# Splitting the dataset into the
# Training set and Test set
install.packages('caTools')
library(caTools)
split = sample.split(dataset$Salary, SplitRatio = 0.7)
trainingset = subset(dataset, split == TRUE)
testset = subset(dataset, split == FALSE)
# Fitting Simple Linear Regression to the Training set
lm.r= lm(formula = Salary ~ YearsExperience,
data = trainingset)
coef(lm.r)
# Predicting the Test set results
ypred = predict(lm.r, newdata = testset)
install.packages("ggplot2")
library(ggplot2)
# Visualising the Training set results
ggplot() + geom_point(aes(x = trainingset$YearsExperience,
y = trainingset$Salary), colour = 'red') +
geom_line(aes(x = trainingset$YearsExperience,
y = predict(lm.r, newdata = trainingset)), colour = 'blue') +
ggtitle('Salary vs Experience (Training set)') +
xlab('Years of experience') +
ylab('Salary')
# Visualising the Test set results
ggplot() +
geom_point(aes(x = testset$YearsExperience, y = testset$Salary),
colour = 'red') +
geom_line(aes(x = trainingset$YearsExperience,
y = predict(lm.r, newdata = trainingset)),
colour = 'blue') +
ggtitle('Salary vs Experience (Test set)') +
xlab('Years of experience') +
ylab('Salary')
Salida de coef(lm.r): 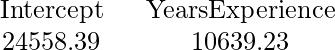
visualización de los resultados del conjunto de entrenamiento:
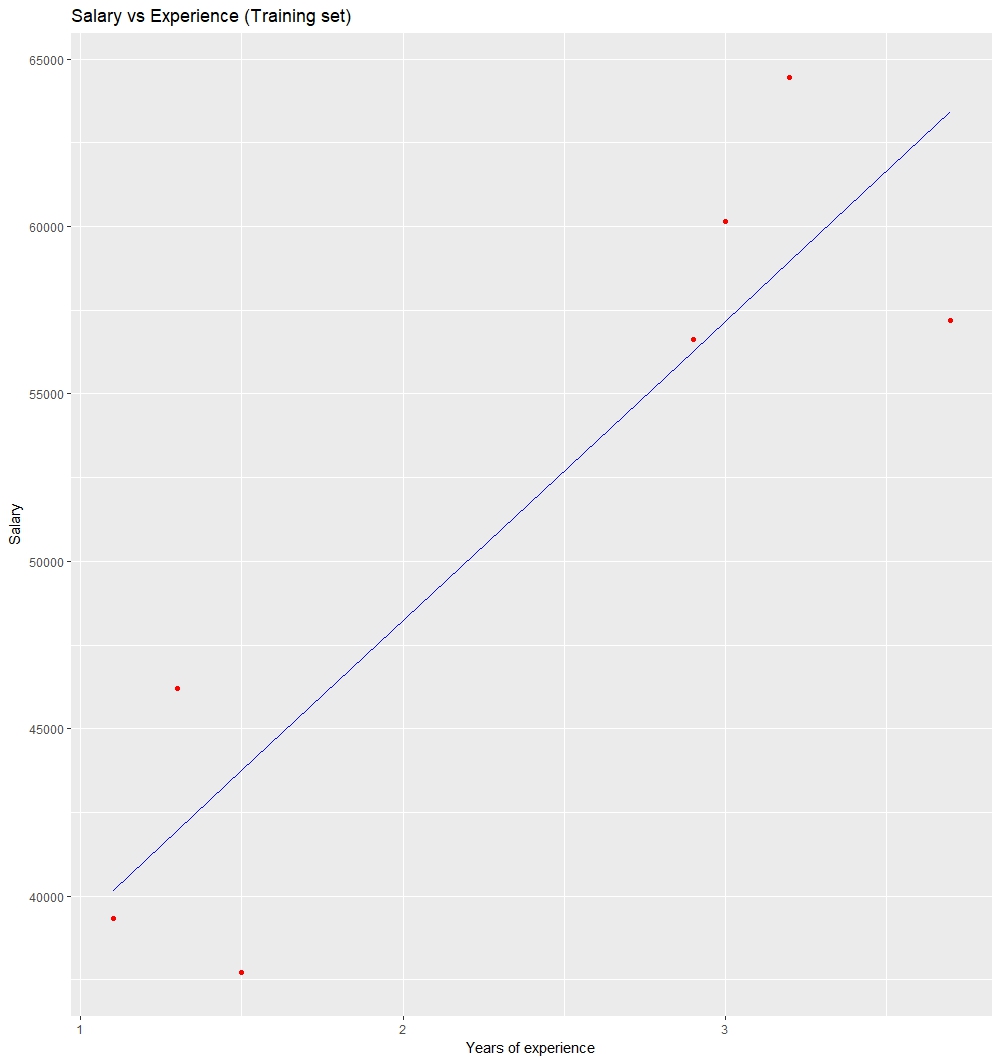
Visualización de los resultados del conjunto de pruebas:
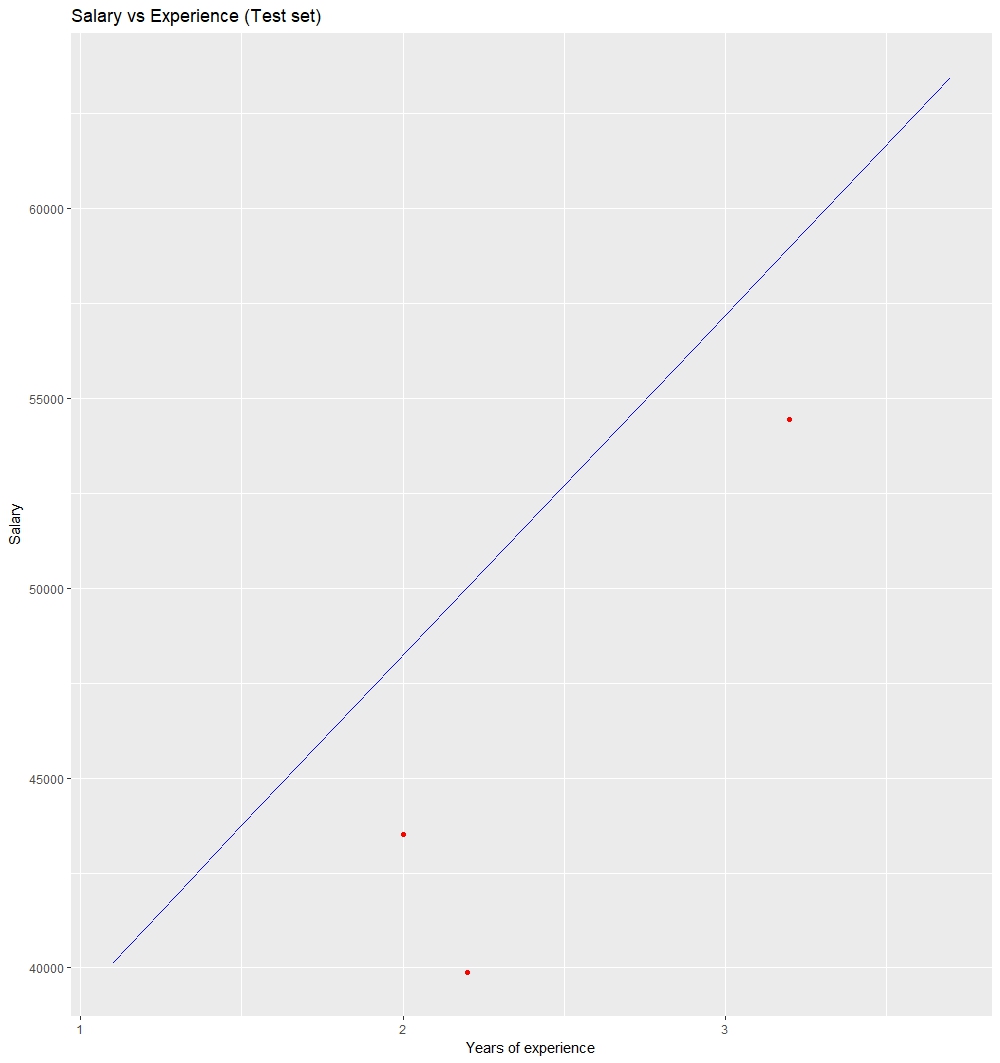
Publicación traducida automáticamente
Artículo escrito por Akashkumar17 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA