ML | Reconocimiento facial mediante Eigenfaces (algoritmo PCA)

En 1991, Turk y Pentland sugirieron un enfoque para el reconocimiento de rostros que utiliza conceptos de álgebra lineal y reducción de dimensionalidad para reconocer rostros. Este enfoque es computacionalmente menos costoso y fácil de implementar y, por lo tanto, se usaba en varias aplicaciones en ese momento, como reconocimiento escrito a mano, lectura de labios, análisis de imágenes médicas, etc.
PCA (Análisis de componentes principales) es una técnica de reducción de dimensionalidad propuesta por Pearson. en 1901. Utiliza valores propios y vectores propios para reducir la dimensionalidad y proyectar una muestra/datos de entrenamiento en un espacio de características pequeño. Veamos el algoritmo con más detalle (en una perspectiva de reconocimiento facial).

Algoritmo de entrenamiento:

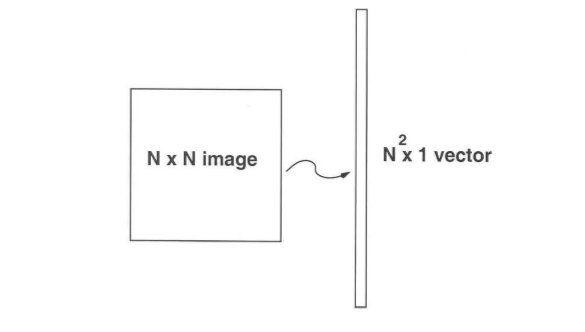
Consideremos un conjunto de m imágenes de dimensión N*N (imágenes de entrenamiento).

Imagen de entrenamiento con True Label (conjunto de datos de personas de LFW)
Primero convertimos estas imágenes en vectores de tamaño N ² tales que:

$x_{1},x_{2},x_{3}...x_{m}$
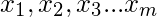
Ahora calculamos el promedio de todos estos vectores de caras y lo restamos de cada vector

$\psi =\dfrac{1}{m}\sum_{i=1}^{m}x_i \\ a_{i} = x_{i}-\psi$

cara_promedio
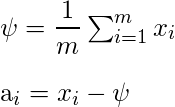
Ahora tomamos todos los vectores de caras para obtener una array de tamaño N ² * M.

$A = \begin{bmatrix} a_{1} &a_{2} &a_{3} &.... & a_{m} \end{bmatrix}$
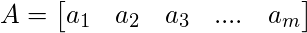
Ahora, encontramos la array de covarianza multiplicando A con A ^T . A tiene dimensiones N ² * M , por lo tanto A ^T tiene dimensiones M * N ² . Cuando multiplicamos esto nos da una array de N ² * N ² , lo que nos da N ² vectores propios de N ² tamaño que no es computacionalmente eficiente para calcular. Así que calculamos nuestra array de covarianza multiplicando A ^T y A . Esto nos da una array M * M que tiene M (suponiendo que M << N ²) vectores propios de tamaño M .

$Cov = A^{T}A$
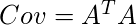
En este paso, calculamos los valores propios y los vectores propios de la array de covarianza anterior utilizando la fórmula a continuación.
$A^{T}A\nu_{i} = \lambda_{i}\nu_{i} \\ \\ AA^{T}A\nu_{i} = \lambda_{i}A\nu_{i} \\ \\ C{}'u_{i} = \lambda_{i}u_{i}$

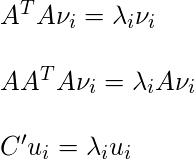
donde,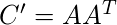
$C{}' = AA^{T}$ y $u_{i} = A\nu_{i}$

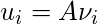
De la declaración anterior se puede concluir que 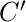$C_{}'$ y C tienen los mismos valores propios y sus vectores propios están relacionados por la ecuación $u_{i} = A\nu_{i}$ . Por lo tanto, los M valores propios (y vectores propios) de la array de covarianza dan los M valores propios (y vectores propios) más grandes de $C_{}'$
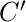
Ahora calculamos el vector propio y los valores propios de esta array de covarianza reducida y los mapeamos 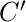$C_{}'$ usando la fórmula $u_{i} = A\nu_{i}$ .
Ahora seleccionamos los vectores propios de K 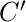$C_{}'$ correspondientes a los valores propios más grandes de K (donde K < M). Estos vectores propios tienen tamaño N ² .
En este paso usamos los vectores propios que obtuvimos en el paso anterior. Tomamos las caras de entrenamiento normalizadas (cara – cara promedio) 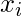$x_{i}$ y representamos cada vector de cara en la combinación lineal de los mejores vectores propios de K (como se muestra en el diagrama a continuación).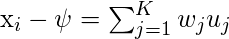

$x_{i} -\psi = \sum_{j=1}^{K} w_{j}u_{j}$

Estos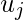 $u_{j}$ se llaman EigenFaces .

caras propias
En este paso, tomamos el coeficiente de caras propias y representamos las caras de entrenamiento en forma de un vector de esos coeficientes. $x_{i} = \begin{bmatrix} w_{1}^i\\ w_{2}^i\\ w_{3}^i\\ .\\ . \\ w_{k}^i \end{bmatrix}$

Combinación lineal de caras propias

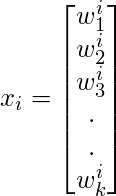
Algoritmo de prueba/detección:

Imágenes de prueba con etiquetas verdaderas

Dada una cara desconocida y , primero debemos preprocesar la cara para que quede centrada en la imagen y tenga las mismas dimensiones que la cara de entrenamiento.
Ahora, restamos la cara de la cara promedio $\psi$ .

$\phi = y - \psi$

Imágenes de prueba – Imágenes promedio
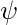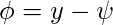
Ahora, proyectamos el vector normalizado en el espacio propio para obtener la combinación lineal de caras propias.

$\phi = \sum_{i=1}^{k}w_{i}u_{i}$
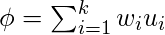
A partir de la proyección anterior, generamos el vector del coeficiente tal que

$\Omega= \begin{bmatrix} w_{1}\\ w_{2}\\ w_{3}\\ .\\ .\\ w_{k} \end{bmatrix}$
Tomamos el vector generado en el paso anterior y lo restamos de la imagen de entrenamiento para obtener la distancia mínima entre los vectores de entrenamiento y los vectores de prueba.

$e_r = min_{l}\left \| \Omega - \Omega_{l}\right \|$

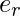Si $e_r$ está por debajo del nivel de tolerancia T _r , entonces se reconoce con l rostro de la imagen de entrenamiento; de lo contrario, el rostro no coincide con ninguno de los rostros del conjunto de entrenamiento.

Imágenes de prueba Con predicción

ventajas:

Fácil de implementar y computacionalmente menos costoso.
No se requiere conocimiento (como rasgos faciales) de la imagen (excepto identificación).

Limitaciones:

Se requiere una cara correctamente centrada para el entrenamiento/prueba.
El algoritmo es sensible a la iluminación, las sombras y también la escala de la cara en la imagen.
Se requiere una vista frontal de la cara para que este algoritmo funcione correctamente.

Referencia :

Artículo de Turk y Pentland de 1991 sobre reconocimiento facial

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta