Los triángulos son polígonos cerrados de tres lados formados por la intersección de tres líneas. Se encuentra mucho en la vida cotidiana. Es una de las formas básicas de la geometría. Tiene tres lados, tres ángulos y tres vértices. Un Triángulo Rectángulo es aquel en el que uno de los ángulos es siempre igual a 90°. El teorema de Pitágoras se deriva para triángulos rectángulos, que establece que el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de la base y la perpendicular.
Dada la longitud de al menos dos lados de un triángulo rectángulo, podemos encontrar el valor de cualquier ángulo del triángulo rectángulo. Para esto, usamos varias funciones trigonométricas como seno, coseno, tangente, cotangente, sec y cosec. Estos nos ayudan a relacionar los ángulos de un triángulo rectángulo con sus lados.
Propiedades
- Hay un vértice en ángulo recto entre los tres vértices.
- El lado opuesto al vértice del ángulo recto se llama hipotenusa .
- La longitud de los lados sigue el teorema de Pythororus, que establece
hipotenusa 2 = base 2 + altura 2
- La hipotenusa es el lado más largo de un triángulo rectángulo.
- Los ángulos que no sean el ángulo recto son ángulos agudos ya que el valor es menor de 90 o
Funciones trigonométricas
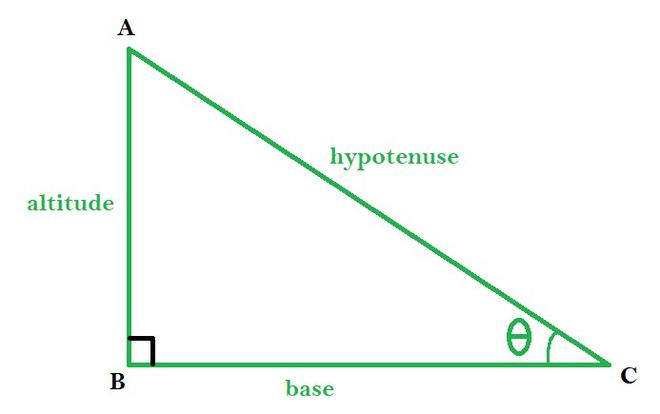
ABC es un triángulo rectángulo con ∠B como ángulo recto
- cosθ: Da la razón de la base por la hipotenusa de un triángulo rectángulo.
cosθ = base / hipotenusa
- senθ: Esto da la relación de la altura por la hipotenusa de un triángulo rectángulo.
sinθ = altitud / hipotenusa
- tanθ: Es la razón de la altura por la base de un triángulo rectángulo.
tanθ = altitud / base
- cotθ: Es el inverso de tanθ
- secθ: Es el inverso de cosθ
- cosecθ: Es el inverso de sinθ
Para encontrar los ángulos de un triángulo rectángulo, podemos tomar el inverso trigonométrico de la razón de los lados dados del triángulo.
Ejemplo:
Si senθ = x, entonces podemos escribir
θ = sen -1 x.
Esto devuelve el ángulo para el cual el valor del seno del ángulo es x.
De manera similar, existe cos -1 θ, tan -1 θ, cot -1 θ, sec -1 θ y cosec -1 θ
Problemas de muestra
Pregunta 1. Dado un triángulo rectángulo, con base igual a 10 cm e hipotenusa igual a 20 cm. Encuentra el valor del ángulo base.
Solución:
Dado, Base = 10cm
Hipotenusa = 20cm
Sea θ el valor del ángulo base. Podemos escribir
cosθ = base / hipotenusa = 10/20 = 1/2
θ = cos -1 (1/2) = 60 o
Por lo tanto, el valor del ángulo base es 60 o .
Pregunta 2. Halla el valor de los ángulos de un triángulo rectángulo, dado que uno de los ángulos agudos es el doble del otro.
Solución:
Como sabemos que la suma de los tres ángulos de un triángulo es 180 ° .
Como uno de los ángulos mide 90 ° y uno de los ángulos agudos es el doble del otro, podemos considerarlos como θ y 2θ.
Entonces, podemos escribir
90 ° + θ + 2θ = 180 °
3θ = 180 o – 90 o
3θ = 90o
θ = 90 o /3 = 30 o
2θ = 2 × 30 o = 60 o
Entonces, los ángulos son 30 o , 60 o y 90 o .
Pregunta 3. Encuentra el valor del ángulo de elevación de una escalera de 5 m de largo, dado que la base de la escalera está a una distancia de 3 m de la pared.
Solución:
Dado que la escalera actúa como una hipotenusa de un triángulo rectángulo y la distancia de la base es igual a 3 m, podemos escribir
Hipotenusa = 5m
Fondo = 3m
Sea el ángulo de elevación θ. Entonces, podemos escribir
cosθ = Base / Hipotenusa = 3/5
θ = cos -1 (3/5)
θ = 53 o
Así, el valor del ángulo de elevación es 53 o .
Pregunta 4. Encuentra el valor de la hipotenusa, dado que la longitud de la altura es de 8 m y el ángulo de la base es de 30 o .
Solución:
Dado que el ángulo de la base es igual a 30 o y la altura es igual a 8 m, podemos aplicar la función seno para encontrar la longitud de la hipotenusa.
sen30 o = altitud / hipotenusa
hipotenusa = altura / sen30 o
Como el valor de sen30 o es igual a 1/2, podemos escribir
hipotenusa = altitud / (1/2) = 2 × altitud
Entonces, hipotenusa = 2 × 8 = 16m
Por tanto, la longitud de la hipotenusa es igual a 16m.