Recuento de números distintos que se pueden formar con el caballo de ajedrez en N movimientos en un teclado móvil

Dado un número entero N y un caballo de ajedrez colocado en el teclado del móvil. La tarea es contar el total de números de N dígitos distintos que puede formar el caballo de ajedrez con N movimientos. Como la respuesta puede ser muy grande dé el valor de módulo de respuesta 10 ⁹ + 7 .

Nota: En cada movimiento, un caballo de ajedrez puede mover 2 unidades horizontalmente y una unidad verticalmente o dos unidades verticalmente y una unidad horizontalmente.

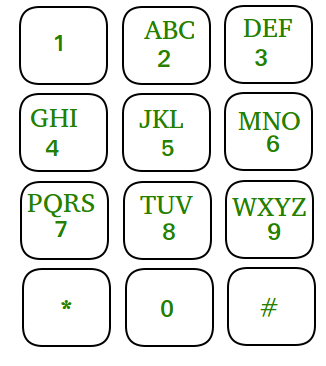
En la imagen se muestra un teclado móvil de demostración donde ‘*’ y ‘#’ no se consideran parte de un número.

Ejemplos:

Entrada: N = 1
Salida: 10
Explicación: Es suficiente colocar el caballo sobre cualquier celda numérica de las 10 celdas.

Entrada: N = 2
Salida: 20
Explicación: Todos los números válidos son [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Enfoque: La idea es encontrar las posibles celdas a las que se puede llegar desde una celda dada para cada celda y sumarlas todas para encontrar la respuesta. Siga los pasos a continuación para resolver el problema:

• Inicialice el vector v[10, 1] y temp[10] .
• Itere sobre el rango [1, N) usando la variable i y realice las siguientes tareas:
  • Encuentre los valores para todas las celdas en temp[] y luego guárdelos en el vector v[].
• Inicialice la suma variable como 0 para almacenar la respuesta.
• Itere sobre el rango [0, 10) usando la variable i y realice las siguientes tareas:
  • Agregue el valor de v[i] a la variable sum .
• Después de realizar los pasos anteriores, imprima el valor de sum como respuesta.

A continuación se muestra la implementación del enfoque anterior.

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the total number of ways
int knightCalling(int N)
{
    int mod = 1000000007;
 
    // Base Case
    if (N == 1)
        return 10;
    vector<int> v(10, 1);
    vector<int> temp(10);
 
    // No cell can be reached from a
    // cell with value 5
    v[5] = 0;
    for (int i = 1; i < N; i++)
    {
       
        // Find the possible values from all cells
        temp[0] = (v[4] + v[6]) % mod;
        temp[1] = (v[6] + v[8]) % mod;
        temp[2] = (v[7] + v[9]) % mod;
        temp[3] = (v[4] + v[8]) % mod;
        temp[4] = (v[0] + v[3] + v[9]) % mod;
        temp[6] = (v[0] + v[1] + v[7]) % mod;
        temp[7] = (v[2] + v[6]) % mod;
        temp[8] = (v[1] + v[3]) % mod;
        temp[9] = (v[2] + v[4]) % mod;
 
        // Store them
        for (int j = 0; j < 10; j++)
            v[j] = temp[i];
    }
 
    // Find the answer
    int sum = 0;
    for (int i = 0; i < 10; i++)
        sum = (sum + v[i]) % mod;
    return sum;
}
 
// Driver Code
int main()
{
    int N = 2;
    cout << knightCalling(N);
}
 
// This code is contributed by Samim Hossain Mondal.

// Java program for the above approach
import java.util.*;
class GFG{
 
// Function to find the total number of ways
static int knightCalling(int N)
{
    int mod = 1000000007;
 
    // Base Case
    if (N == 1)
        return 10;
    int []v = new int[10];
    int []temp = new int[10];
    Arrays.fill(v, 1);
 
    // No cell can be reached from a
    // cell with value 5
    v[5] = 0;
    for (int i = 1; i < N; i++)
    {
       
        // Find the possible values from all cells
        temp[0] = (v[4] + v[6]) % mod;
        temp[1] = (v[6] + v[8]) % mod;
        temp[2] = (v[7] + v[9]) % mod;
        temp[3] = (v[4] + v[8]) % mod;
        temp[4] = (v[0] + v[3] + v[9]) % mod;
        temp[6] = (v[0] + v[1] + v[7]) % mod;
        temp[7] = (v[2] + v[6]) % mod;
        temp[8] = (v[1] + v[3]) % mod;
        temp[9] = (v[2] + v[4]) % mod;
 
        // Store them
        for (int j = 0; j < 10; j++)
            v[i] = temp[i];
    }
 
    // Find the answer
    int sum = 0;
    for (int i = 0; i < 10; i++)
        sum = (sum + v[i]) % mod;
    return sum;
}
 
// Driver Code
public static void main(String[] args)
{
    int N = 2;
    System.out.print(knightCalling(N));
}
}
 
// This code is contributed by 29AjayKumar

# Python 3  program for the above approach
 
# Function to find the total number of ways
def knightCalling(N):
 
    mod = 1000000007
 
    # Base Case
    if (N == 1):
        return 10
    v = [1]*10
    temp = [0]*10
 
    # No cell can be reached from a
    # cell with value 5
    v[5] = 0
    for i in range(1, N):
       
        # Find the possible values from all cells
        temp[0] = (v[4] + v[6]) % mod
        temp[1] = (v[6] + v[8]) % mod
        temp[2] = (v[7] + v[9]) % mod
        temp[3] = (v[4] + v[8]) % mod
        temp[4] = (v[0] + v[3] + v[9]) % mod
        temp[6] = (v[0] + v[1] + v[7]) % mod
        temp[7] = (v[2] + v[6]) % mod
        temp[8] = (v[1] + v[3]) % mod
        temp[9] = (v[2] + v[4]) % mod
 
        # Store them
        for j in range(10):
            v[j] = temp[j]
 
    # Find the answer
    sum = 0
    for i in range(10):
        sum = (sum + v[i]) % mod
    return sum
 
# Driver Code
if __name__ == "__main__":
 
    N = 2
    print(knightCalling(N))
 
    # This code is contributed by ukasp.

// C# program for the above approach
using System;
class GFG{
 
  // Function to find the total number of ways
  static int knightCalling(int N)
  {
    int mod = 1000000007;
 
    // Base Case
    if (N == 1)
      return 10;
    int []v = new int[10];
    int []temp = new int[10];
    for(int i = 0; i < 10; i++) {
      v[i] = 1;
    }
 
    // No cell can be reached from a
    // cell with value 5
    v[5] = 0;
    for (int i = 1; i < N; i++)
    {
 
      // Find the possible values from all cells
      temp[0] = (v[4] + v[6]) % mod;
      temp[1] = (v[6] + v[8]) % mod;
      temp[2] = (v[7] + v[9]) % mod;
      temp[3] = (v[4] + v[8]) % mod;
      temp[4] = (v[0] + v[3] + v[9]) % mod;
      temp[6] = (v[0] + v[1] + v[7]) % mod;
      temp[7] = (v[2] + v[6]) % mod;
      temp[8] = (v[1] + v[3]) % mod;
      temp[9] = (v[2] + v[4]) % mod;
 
      // Store them
      for (int j = 0; j < 10; j++)
        v[j] = temp[i];
    }
 
    // Find the answer
    int sum = 0;
    for (int i = 0; i < 10; i++)
      sum = (sum + v[i]) % mod;
    return sum;
  }
 
  // Driver Code
  public static void Main()
  {
    int N = 2;
    Console.Write(knightCalling(N));
  }
}
 
// This code is contributed by Samim Hossain Mondal.

<script>
       // JavaScript code for the above approach
 
       // Function to find the total number of ways
       function knightCalling(N) {
           let mod = 1000000007;
 
           // Base Case
           if (N == 1)
               return 10;
           let v = new Array(10).fill(1)
           let temp = new Array(10).fill(0);
 
           // No cell can be reached from a
           // cell with value 5
           v[5] = 0;
           for (let i = 1; i < N; i++)
           {
            
               // Find the possible values from all cells
               temp[0] = (v[4] + v[6]) % mod;
               temp[1] = (v[6] + v[8]) % mod;
               temp[2] = (v[7] + v[9]) % mod;
               temp[3] = (v[4] + v[8]) % mod;
               temp[4] = (v[0] + v[3] + v[9]) % mod;
               temp[6] = (v[0] + v[1] + v[7]) % mod;
               temp[7] = (v[2] + v[6]) % mod;
               temp[8] = (v[1] + v[3]) % mod;
               temp[9] = (v[2] + v[4]) % mod;
 
               // Store them
               for (let i = 0; i < 10; i++)
                   v[i] = temp[i];
           }
 
           // Find the answer
           let sum = 0;
           for (let i = 0; i < 10; i++)
               sum = (sum + v[i]) % mod;
           return sum;
       }
 
       // Driver Code
       let N = 2;
       document.write(knightCalling(N));
 
 // This code is contributed by Potta Lokesh
   </script>

20

Complejidad temporal: O(N)
Espacio auxiliar: O(1)