Espacio nulo y nulidad de una array

Espacio nulo y nulidad son conceptos en álgebra lineal que se utilizan para identificar la relación lineal entre atributos.

Espacio nulo:

El espacio nulo de cualquier array A consta de todos los vectores B tales que AB = 0 y B no es cero. También se puede pensar como la solución obtenida de AB = 0 donde A es una array de tamaño conocido m x ny B es una array de tamaño por encontrar n x k. El tamaño del espacio nulo de la array nos proporciona el número de relaciones lineales entre atributos.

Una descripción generalizada:

Sea una array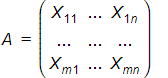

y hay un vector en el espacio nulo de A, es decir,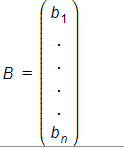

entonces B satisface las ecuaciones dadas,

La idea –

1. AB = 0 implica que cada fila de A cuando se multiplica por B va a cero.
2. Los valores de las variables en cada muestra (representados por una fila) se comportan de la misma manera.
3. Esto ayuda a identificar las relaciones lineales en los atributos.
4. Todo vector espacial nulo corresponde a una relación lineal.

Nulidad:

La nulidad se puede definir como el número de vectores presentes en el espacio nulo de una array dada. En otras palabras, la dimensión del espacio nulo de la array A se denomina nulidad de A. El número de relaciones lineales entre los atributos viene dado por el tamaño del espacio nulo. Los vectores de espacio nulo B se pueden utilizar para identificar estas relaciones lineales.

Teorema de nulidad de rango:
El teorema de nulidad de rango nos ayuda a relacionar la nulidad de la array de datos con el rango y el número de atributos en los datos. El teorema de nulidad de rango viene dado por:

Nulidad de A + Rango de A = Número total de atributos de A (es decir, número total de columnas en A)

Rango:
El rango de una array se refiere al número de filas o columnas linealmente independientes de la array.

Ejemplo con prueba del teorema de nulidad de rango:

Consider the matrix A with attributes {X1, X2, X3}
    1  2  0
A = 2  4  0
    3  6  1
then,
Number of columns in A = 3

R1 and R3 are linearly independent.
The rank of the matrix A which is the 
number of non-zero rows in its echelon form are 2.
we have,
AB = 0

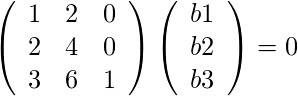Then we get,
b1 + 2*b2 = 0
b3 = 0
The null vector we can get is 

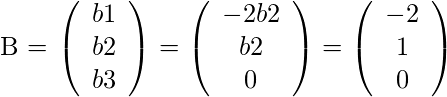The number of parameter in the general solution is the dimension 
of the null space (which is 1 in this example). Thus, the sum of 
the rank and the nullity of A  is 2 + 1 which
is equal to the number of columns of A.

Esta relación de rango y nulidad es válida para cualquier array.

Ejemplo de Python para encontrar el espacio nulo de una array:

# Sympy is a library in python for 
# symbolic Mathematics
from sympy import Matrix
  
# List A 
A = [[1, 2, 0], [2, 4, 0], [3, 6, 1]]
  
# Matrix A
A = Matrix(A)
  
# Null Space of A
NullSpace = A.nullspace()   # Here NullSpace is a list
  
NullSpace = Matrix(NullSpace)   # Here NullSpace is a Matrix
print("Null Space : ", NullSpace)
  
# checking whether NullSpace satisfies the
# given condition or not as A * NullSpace = 0
# if NullSpace is null space of A
print(A * NullSpace)

Producción:

Null Space :  Matrix([[-2], [1], [0]])
Matrix([[0], [0], [0]])

Ejemplo de Python para encontrar la nulidad de una array:

from sympy import Matrix
  
A = [[1, 2, 0], [2, 4, 0], [3, 6, 1]]
   
A = Matrix(A)
  
# Number of Columns
NoC = A.shape[1]
  
# Rank of A
rank = A.rank()
  
# Nullity of the Matrix
nullity = NoC - rank
  
print("Nullity : ", nullity)

Producción:

Nullity :  1