En matemáticas, la aritmética se ocupa del estudio de los números, manteniendo el énfasis en las operaciones tradicionales relevantes para ellos. Estos operadores son suma, resta, multiplicación, división, exponentes y radicales. La aritmética puede afirmarse con seguridad como la base de todas las demás ramas de las matemáticas. Geometría, medición, trigonometría, etc., todos estos campos emplean las operaciones aritméticas básicas para varias observaciones matemáticas, cálculos y conclusiones.
Serie
La suma de todos los términos de una secuencia dada forma una serie de la secuencia en cuestión. Así, una serie es básicamente una sucesión, solo que con un operador de suma entre todos sus términos. Ahora, dado que una serie se ha formado a partir de una secuencia en sí, es natural que su patrón sea exactamente el mismo que su secuencia principal. Una serie sería definida o indefinida dependiendo también de la secuencia en cuestión.
Ejemplos
- 1 + 2 + 3 + 4 + …. es una serie infinita de todos los números naturales.
- 10 + 20 + 30 + 40 es una serie finita de los primeros cuatro múltiplos de 10.
Serie geométrica infinita
Una serie en la que cada término subsiguiente está en una proporción constante con respecto a su término anterior se denomina serie geométrica. De la definición de una serie, es claro que todos los términos que constituyen una serie son en suma entre sí. Una serie infinita es aquella que no tiene fin. Implica que en una serie geométrica infinita, los términos están en una proporción constante entre sí y no tienen fin. Cabe señalar que la razón es continua, es decir, constante a lo largo de la serie y se denomina razón común. Otro aspecto importante a tener en cuenta es que el valor absoluto de la razón común debe ser mayor que cero, es decir, |r| < 0.
En general, una serie geométrica finita con su primer término a, y razón común r se expresa como,
a, ar, ar 2 , ar3, ar 4 , …ar n – 2 , ar n – 1 , ar n .
Sin embargo, una serie geométrica infinita se representaría de la siguiente manera,
a, a r , ar 2 , ar 3 , ar 4 , …ar 100000 ,…
Por ejemplo, la serie 2 + 4 + 8 + 16 + 32 +…. es una serie geométrica infinita porque cada término sucesivo se obtiene multiplicando el término anterior por 2, y dado que la serie no tiene fin, es decir, no es finita.
Encuentra la razón común de una serie geométrica infinita.
Responder:
En lenguaje sencillo, la razón común de una serie geométrica significa la cantidad que se multiplica por cada término precedente para formar el término siguiente. Esto significa que cada término después del primero debe multiplicarse por una cantidad fija para formar una serie geométrica infinita. También implica que si uno tuviera que dividir cada término sucesivo con el término inmediatamente anterior, el cociente así obtenido sería la razón común de la serie dada. Esto se debe a la regla general de división en matemáticas. El divisor multiplicado por el cociente da como resultado el dividendo. Aquí, las palabras divisor, cociente y dividendo pertenecen al término anterior, razón común y términos sucesivos respectivamente. La razón común, r de una serie geométrica se calcula usando la siguiente fórmula,
r =
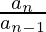
Donde n representa el término subsiguiente y n – 1 es el término que precede inmediatamente al término elegido.
Cabe señalar que para calcular la razón común, se puede tomar cualquier término aleatorio de la serie dada y dividirlo por su término inmediatamente anterior, y el cociente sería constante en toda la serie, de ahí el nombre de «razón común». ‘.
Ejemplos
- La razón común de la serie 3, 9, 27, 81, 243, 729, ….. es = 9/3 = 27/9 = 81/27 = 243/81 = 729/243 =3 .
- La razón común de la serie geométrica 10, 100, 1000, 10000,… sería = 100/10 = 1000/100 = 10.
- La razón común de la serie 56, 28, 14, 7,… sería = 56/2 = 28/14 = 14/7 = 2.
Problemas similares
Pregunta 1: Encuentra la razón común de la serie: 27, 9, 3, 1, 1/3, 1/9, 1/27, … y enumera los siguientes tres términos.
Solución:
Proporción común =
= 1/3.
Los próximos tres términos serían,
1/27 × 1/3 = 1/81
1/81 × 1/3 = 1/243
1/243 × 1/3 = 1/729
Por lo tanto, la razón común es 1/3 y los siguientes tres términos son 1/81, 1/243, 1/729.
Pregunta 2: Encuentra la razón común de la serie: 5, 25, 125, 625,… y enumera los siguientes dos términos.
Solución:
Razón común =
= 25/5 = 5
Los próximos tres términos serían,
625 × 5 = 3125
3125 × 5 = 15625
Por lo tanto, la razón común es 5 y los siguientes dos términos son 3125 y 15625.
Pregunta 3. Encuentra la razón común de la serie: 25, 5, 1, 1/5, 1/25, … y enumera los siguientes 4 términos.
Solución:
Razón común =
= 5/25 = 1/5
Los próximos 4 términos serían,
1/25 × 1/5 = 1/125
1/125 × 1/5 = 1/625
1/625 × 1/5 = 1/3125
1/3125 × 1/5 = 1/15625
Por lo tanto, la razón común es 1/5 y los siguientes 4 términos son 1/125, 1/625, 1/3125 y 1/15625.
Pregunta 4: Encuentra la razón común de la serie: 1/216, 1/36, 1/6, 1, 6, 36,… y enumera los siguientes 2 términos.
Solución:
Razón común =
=
= 6
Los próximos 2 términos serían,
36 × 6 = 216
216 × 6 = 1296
Por lo tanto, la razón común es 6 y los siguientes 2 términos son 216 y 1296.
Pregunta 5: Encuentra la razón común de la serie: 1, 3, 9, 27, 81, … y enumera los siguientes 4 términos.
Solución:
Razón común =
= 3/1 = 3
Los siguientes 2 términos serían:
81 × 3 = 243
243 × 3 = 729
Por lo tanto, la razón común es 3 y los siguientes 2 términos son 243 y 729.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA