¿A qué equivale ‘i’ en álgebra?

La combinación de Números Reales e Imaginarios se llama Número Complejo. Se representa por ‘Z’. Los números complejos tienen muchas aplicaciones, ya que son particularmente valiosos en hardware, óptica e hipótesis cuánticas para representar ondas. Además, los cambios de Fourier utilizan números complejos. 

Matemáticamente, un número Complejo se representa como Z = a + ib, donde a es la parte Real yb es la parte imaginaria. Aquí, i es el número imaginario y se llama “iota”. Por ejemplo, 5 + 3i, donde 5 es el número real y 3i es el número imaginario. En consecuencia, un número complejo es una representación simple de la expansión de dos números, es decir, un número real y un número imaginario. Una parte es simplemente real (Re) y la otra parte es absolutamente imaginaria (Img).

Hay varias formas de números complejos principalmente 3 tipos, forma rectangular: z = a + ib, forma polar: z = r (cosθ + isinθ), y forma exponencial: z = re (iθ) donde, θ es el ángulo (en radianes) entre el eje real positivo y el segmento de línea que conecta el origen y z.

Numeros reales 

Cualquier número que se pueda trazar en una recta numérica se llama número real. Cada uno de los números negativos y positivos, decimales y parciales se denominan números reales. No incluyen ningún valor imaginario. Se utilizan muy a menudo en la vida práctica para realizar diversas operaciones algebraicas, resolver ecuaciones simples y largas, geometría, etc. Los números reales se indican con ‘R’. Consiste en,

• Números racionales: Un número racional es un número real que está en forma de fracción p/q donde q no es igual a 0. Se denota por ‘ Q ‘. Consiste en decimales terminales y decimales periódicos no terminales y, por lo tanto, no se puede representar en forma fraccionaria. Ejemplo de número racional: 0,53, 4, 5,768, 3/2, 1,2222222… Además, los números racionales contienen cuadrados perfectos como 4, 9, 16, 25, 49, etc.
• Números irracionales: un número irracional es un número real que no se puede representar en forma de fracción o Cuando cualquier número no se puede expresar en forma de cociente al dividir dos números, se lo conoce como número racional denotado por ‘ R – Q ‘ . Consiste en decimales no recurrentes no terminales. Ejemplo de números irracionales: √(2) = 1,41421356…, √(5) = 2,23606…, π.

Números imaginarios (i)

Se define como la raíz cuadrada de números naturales negativos o podemos decir cualquier número que da un número negativo después de elevarlo al cuadrado. Se combinan con números reales para formar números complejos y tienen un gran impacto en la teoría de números y la geometría. También juegan un papel importante en la ingeniería y la vida práctica, por ejemplo, se utilizan en circuitos eléctricos para representar varias cantidades y circuitos físicos y resolver algunas ecuaciones cuadráticas complejas en la física moderna. Ejemplo: √(-2), √(-7), etc.

¿A qué es igual en álgebra?

Responder:

Fue inventado por matemáticos en aquel entonces cuando, al tener problemas para encontrar las raíces de algunas ecuaciones cúbicas, notaron el hecho de que algunos números que hoy se dicen imaginarios no se pueden representar en el eje x, entonces, ¿por qué no usar el eje y para representarlos y así dio lugar al concepto de raíces cuadradas de números negativos, es decir, números imaginarios.

Se denota por ‘i’, donde el valor de i se considera como √(-1). Cualquier número real cuando se multiplica por un número imaginario dará como resultado un número imaginario. Por ejemplo, 5 × √(-1) = √(-5) o 5i. Los números imaginarios, como su nombre indica, en realidad no son imaginarios. Ellos existen. Tomemos un ejemplo:

Supongamos resolver una ecuación cuadrática x ² = -4 . En la ecuación anterior, no se puede encontrar la raíz de -4, lo que implica que no hay raíces reales, es decir, la parábola no corta el eje x como se muestra en el diagrama.

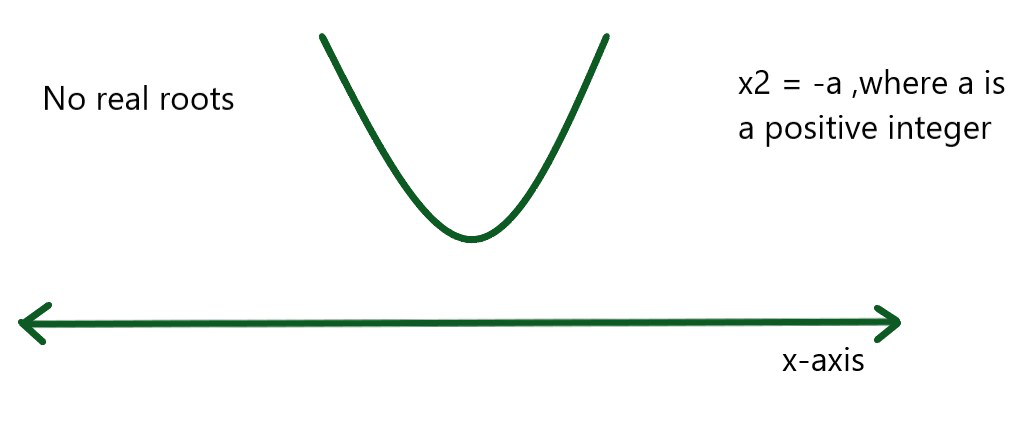
Escribe la ecuación anterior como x ² = -1 × 4. Ahora, sabemos que la raíz cuadrada de 4 es +2 y -2.

Pero no se conocen las raíces cuadradas de -1, por lo que los matemáticos inventaron un nuevo número como √(-1) y lo llamaron ‘i’ (que representa el número imaginario). Ahora se puede resolver la ecuación anterior asumiendo que √(-1) es i y obtenga las raíces respectivas como +2i y -2i.

Evolución de los números imaginarios

Los números imaginarios también se encontraron como todos los demás números en el sistema numérico a medida que surgía su necesidad. Los primeros números naturales se encontraron en la civilización humana temprana que se inventaron para realizar el conteo normal. Luego se inventó el ‘0’ para representar la nada, combinándose con los naturales se les llama números enteros. Después de eso, se inventaron los números negativos que también tienen un significado físico, por ejemplo, representar una deuda o ir en la dirección opuesta.

La combinación de números enteros y números negativos se llama números enteros. Luego vinieron los números racionales, usados ​​para calcular una parte o fracción de algo. Luego, después de un tiempo, los matemáticos griegos encontraron los números irracionales al encontrar la hipotenusa del triángulo rectángulo de base y tamaño de 1 unidad y, finalmente, los números imaginarios se encontraron cuando los matemáticos no pudieron resolver algunas ecuaciones cuadráticas como se discutió en el tema anterior.

Ejemplo de la vida real de número imaginario

Supongamos que un hombre se mueve en una dirección particular con una velocidad X. Después de un tiempo, debido a alguna razón, su dirección se invierte y, por lo tanto, la velocidad se convierte en ‘-X’. Esto significa que si el hombre gira 180 grados, entonces su velocidad se multiplica por ‘-1’. Ahora suponga que si el hombre necesita cambiar su dirección en el camino perpendicular al camino original, entonces necesita girar solo la mitad de la rotación que necesita hacer mientras va en la dirección opuesta. Representemos esta rotación por r.

Considerando el ejemplo anterior, podemos decir que r ^. r = -1. (Ya que dos rotaciones de 90° = una rotación de 180°). Después de dar un giro de 90°, la nueva velocidad del hombre será Xr, donde r = √(-1) (número imaginario). 

Problemas de muestra

Pregunta 1: ¿Cuáles de los siguientes entre los números dados son números imaginarios?

1. -1 
2. √7                      
3. 2√-1                  
4. 3i
5. √-4 
6. √(-1) ²                       

Solución: 

3, 4, 5, son números imaginarios ya que todos tienen números negativos en raíz cuadrada. 

Pregunta 2: Halla los valores de los siguientes términos,

1. yo ²                    
2. yo ³               
3. yo ⁴        
4. yo ⁵
5. yo ⁶                   
6. yo ²⁷¹             
7. yo ⁷⁴      
8. yo ^-1 

Solución: 

1. yo ² = -1
2. yo ³ = yo
3. yo ⁴ = 1       
4. yo ⁵ = yo 
5. yo ⁶ = -1
6. yo ²⁷¹  = yo ^{4 x 67} .i ³ = 1 × yo = yo    
7. i ⁷⁴   = i ^{4 x 18} .i ² = 1 × -1 = -1
8. i ^-1   = 1/i (multiplicando numerador y denominador por i => i/i ² = i/-1 = -i)

Pregunta 3: Escribe la parte imaginaria de los números complejos dados.

1. 4 + 3√-1                 
2. yo ² + yo             
3. √7 + 6i                        
4. -4 + 2i            

Solución:    

1. 3
2. 1              
3. 6
4. 2

Pregunta 4: Reduce los siguientes números imaginarios como el múltiplo de i o √(-1).

1. √(-9)             
2. 5√(-3)        
3. 6i ²                        
4. 3√(-4) ³

Solución: 

1. √(-9) = 3√-1 = 3i
2. 5√(-3) = 5√3√-1 = 5√3i
3. 6i ³ = 6i (ya que iii = i)
4. 3√(-2) ³ = 3 × 2√2√-1 = 6√2i