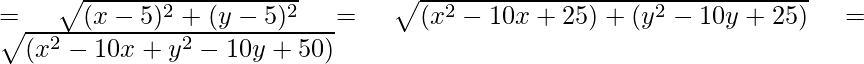Encuentra una relación entre x e y tal que el punto (x, y) sea equidistante de los puntos (7, 1) y (3, 5)

Las matemáticas están relacionadas con los números y los cálculos. Las matemáticas se dividen en diferentes ramas según el tipo de operaciones o cálculos como álgebra, geometría, aritmética, etc. Geometría Es la rama de las matemáticas que se ocupa de la forma y sus propiedades. La geometría que se ocupa de puntos, líneas y planos en los que intervienen coordenadas se denomina geometría de coordenadas.

Coordenadas

La ubicación de cualquier punto en un plano se puede expresar como (x, y) y estos pares se denominan coordenadas de ese punto, x es el valor horizontal de un punto en el plano. Este valor también se puede llamar coordenada x o abscisa, y es el valor vertical de un punto en el plano. Este valor se puede llamar la coordenada y o la ordenada . En geometría de coordenadas, el punto se representa en el plano cartesiano.

plano cartesiano

Es un plano formado por dos rectas perpendiculares que es el eje x (eje horizontal) y el eje y (eje vertical). La posición de un punto en el plano cartesiano se puede representar mediante el par ordenado (x, y).

Fórmula de distancia

Esta fórmula se utiliza para calcular la distancia entre dos puntos en un plano. En otras palabras, da la longitud del segmento de línea que se puede formar después de unir dos puntos. Sean los dos puntos A y B, cuyas coordenadas sean (x ₁ , y ₁ ) y (x ₂ , y ₂ ) respectivamente. Entonces, la distancia entre dos puntos se da como,

Distancia (d)= $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1 )^2}$

Encuentre la relación entre x e y tal que el punto (x, y) sea equidistante de (7, 1) y (3, 5).

Solución:

Equidistante significa que tiene la misma distancia. (x, y) es equidistante del punto (7, 1) y (3, 5), lo que significa que la distancia del punto (x, y) desde ambos puntos es igual.

Supongamos que A y B son los nombres de los puntos (7, 1) y (3, 5) respectivamente y C el punto que tiene las coordenadas (x, y).

Entonces, según la pregunta, d ₁ y d ₁ son iguales.

CB = CA

Use la fórmula de distancia para encontrar los valores d ₁ y d _{2 .}

AC (Distancia entre (x, y) y (7, 1))

= $\sqrt{(x - 7)^2 + (y- 1 )^2}$

= $\sqrt{(x^2 -14x +49) + (y^2-2y+1) = \sqrt{(x^2 + 14x + y^2 -2y +50 )}$

CB (Distancia entre (x, y) y (3, 5))

= $\sqrt{(x-3)^2+(y-5)^2}$

= $\sqrt{(x^2-6x+9)+(y^2-10y+25)}$

= $\sqrt{(x^2-6x+y^2-10y+34)}$

Como, CB = CA

$\sqrt{(x^2-14x+y^2-2y+50)} = \sqrt{(x^2-6x+y^2-10y+34)}$

Cuadrando ambos lados,

(x2 – 14x + y2 ^–^2y + 50) = (x2 – 6x + ^y2^– 10y + 34)

x2 – x2 ⁺^y2 – y2 – 14x ⁺ 6x – 2y + 10y = 34 – ⁵⁰

-8x + 8y = -16

8x – 8y = 16

x – y = 2

x = 2 + y

Por lo tanto, la relación entre x e y tal que el punto (x, y) es equidistante de (7, 1) y (3, 5) es x = 2 + y

Problemas de muestra

Pregunta 1: Encuentra la relación entre x e y tal que el punto (x, y) sea equidistante de (-5, -5) y (5, 5).

Solución:

Equidistante significa que tiene la misma distancia. (x, y) es equidistante del punto (-5, -5) y (5, 5), lo que significa que la distancia del punto (x, y) desde ambos puntos es igual.

Supongamos que A y B son el nombre del punto (-5, -5) y (5, 5) respectivamente y C el punto que tiene las coordenadas (x, y).

Entonces, según la pregunta, d ₁ y d ₂ son iguales.

CB = CA

Use la fórmula de distancia para encontrar los valores d ₁ y d _{2 .}

AC (Distancia entre (x , y) y (-5, -5))

$\sqrt{(x^2-14x+y^2-2y+50)} = \sqrt{(x^2-6x+y^2-10y+34)}$

CB (Distancia entre (x , y) y (5 , 5))

$= \sqrt{(x-5)^2+(y-5)^2} = \sqrt{(x^2-10x+25)+(y^2-10y+25)} = \sqrt{(x^2-10x+y^2-10y+50)}$

Como, CB = CA

$\sqrt{(x^2-10x+y^2-10y+50)} = \sqrt{(x^2+10x+y^2+10y+50)}$

Cuadrando ambos lados,

(x ² – 10x + y ² – 10y + 50) = (x ² + 10x + y ² + 10y + 50)

x2 – x2 + ^y2 – ^y2^{= 10x}⁺ 10x + 10y + 10y + 50 – 50

0 = 20x + 20y

x = -y

Por lo tanto, la relación entre x e y tal que el punto (x, y) es equidistante de (-5, -5) y (5, 5) es x = -y

Pregunta 2: Encuentra la relación entre x e y tal que el punto (x, y) sea equidistante de (-2, 0) y (2, 0).

Solución:

(x, y) es equidistante del punto (-2, 0) y (2, 0), lo que significa que la distancia del punto (x, y) desde ambos puntos es igual. Supongamos que A y B son el nombre del punto (-2, 0) y (2, 0) respectivamente y C el punto que tiene coordinadas (x, y). Entonces, según la pregunta, CB y AC son iguales.

CB = CA

Usa la fórmula de la distancia para encontrar las distancias CB y AC.

AC (Distancia entre (x, y) y (-2, -0))

$= \sqrt{(x-(-2)^2+(y-0)^2} = \sqrt{(x + 2)^2 + (y )^2} = \sqrt{(x^2+ 4x + 4)+(y^2 )}$

CB (Distancia entre (x, y) y (2, 0))

$= \sqrt{(x-2)^2+(y-0)^2} = \sqrt{(x^2-4x+4)+(y^2)}$

Como, CB = CA

\sqrt(x^2-4x+4)+(y^2) = \sqrt(x^2+ 4x + 4)+(y^2 )

Cuadrando ambos lados,

(x2 – 4x + 4) + (y2 ⁾⁼ (x2 ⁺ 4x + 4) + ( ^y2 )

x2 – x2 + y2 ^– y2 ⁼^4x⁺ 4x + 4 – 4

0 = 8x

x = 0

x = 0 significa eje y.

Por lo tanto, todos los puntos que se encuentran en el eje y son equidistantes del punto (-2, 0) y (2, 0).

Por lo tanto, la relación entre x e y tal que el punto (x, y) es equidistante de (-2, 0) y (2, 0) es x = 0

Publicación traducida automáticamente

Artículo escrito por romy421kumari y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Coordenadas

plano cartesiano

Fórmula de distancia

Encuentre la relación entre x e y tal que el punto (x, y) sea equidistante de (7, 1) y (3, 5).

Problemas de muestra

Deja una respuesta Cancelar la respuesta