Requisito previo : algoritmo a priori y minería de conjunto de elementos frecuentes
El número de conjuntos de elementos frecuentes generados por el algoritmo Apriori a menudo puede ser muy grande, por lo que es beneficioso identificar un pequeño conjunto representativo del que se pueda derivar cada conjunto de elementos frecuentes. Uno de estos enfoques es el uso de conjuntos de elementos frecuentes máximos.
Un conjunto de elementos frecuente máximo es un conjunto de elementos frecuente para el cual ninguno de sus superconjuntos inmediatos es frecuente. Para ilustrar este concepto, considere el siguiente ejemplo:
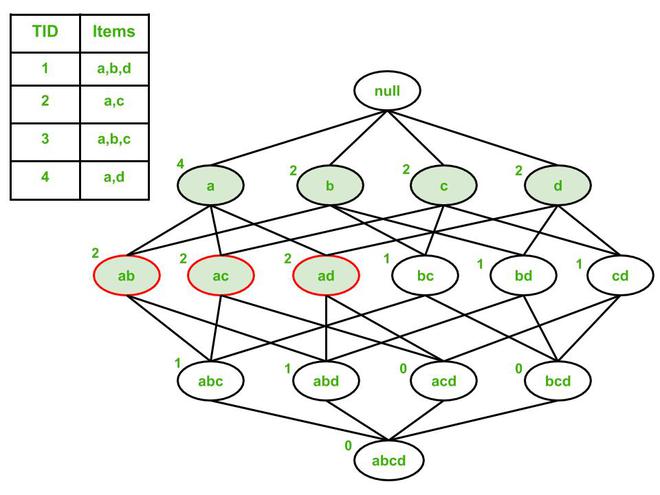
Los recuentos de soporte se muestran en la parte superior izquierda de cada Node. Suponga que el umbral de recuento de soporte = 50% , es decir, cada artículo debe ocurrir en 2 o más transacciones. Según ese umbral, los conjuntos de elementos frecuentes son: a, b, c, d, ab, ac y ad (Nodes sombreados).
De estos 7 conjuntos de elementos frecuentes, 3 se identifican como de máxima frecuencia (con un contorno rojo):
- ab : Las superseries inmediatas abc y abd son poco frecuentes.
- ac : Las superseries inmediatas abc y acd son poco frecuentes.
- ad : Las superseries inmediatas abd y acd son poco frecuentes.
Los 4 Nodes frecuentes restantes (a, b, c y d) no pueden ser de frecuencia máxima porque todos tienen al menos 1 superconjunto inmediato que es frecuente.
Ventaja : los conjuntos de
elementos frecuentes máximos proporcionan una representación compacta de todos los conjuntos de elementos frecuentes para un conjunto de datos en particular. En el ejemplo anterior, todos los conjuntos de elementos frecuentes son subconjuntos de los conjuntos de elementos frecuentes máximos, ya que podemos obtener conjuntos a, b, c, d enumerando subconjuntos de ab, ac y ad (incluidos los conjuntos de elementos frecuentes máximos).
Desventaja :
el recuento de soporte de los conjuntos de elementos de frecuencia máxima no proporciona ninguna información sobre el recuento de soporte de sus subconjuntos. Esto significa que se necesita un recorrido adicional de datos para determinar el recuento de soporte para conjuntos de elementos frecuentes no máximos, lo que puede ser indeseable en ciertos casos.