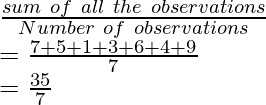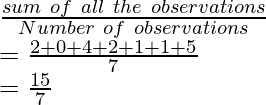¿Cómo calcular la desviación media?

La ciencia de recopilar, analizar y presentar datos se conoce como estadística. En estadística, la desviación se conoce como la variación que se obtiene entre el valor observado y otros valores de una variable. Aprendamos más sobre este tema y aprendamos qué es una desviación de hombres en estadísticas,

Desviación media

La desviación media de una distribución estándar dada es una medida de la tendencia central. Se puede calcular utilizando la media aritmética, la mediana o la moda de los datos. Se utiliza para mostrar a qué distancia se sitúan las observaciones del promedio de las observaciones de datos. Cada una de estas desviaciones se considera un valor absoluto. Esto implica que se ignoran los signos negativos. Además de esto, las desviaciones a ambos lados del valor medio son de naturaleza equivalente. Por lo tanto, la desviación media de la distribución de datos dada es la media de las desviaciones absolutas de las observaciones o valores de un promedio adecuado. Este promedio adecuado puede ser la media, la mediana o la moda de los datos. Por ejemplo, la fórmula de desviación media para una serie individual o una serie continua, etc.

Tipos de desviación media

Series Individuales

Para un conjunto dado de datos sin procesar, cuando los datos se presentan individualmente en forma de serie, se conoce como serie individual. Es básicamente una secuencia de datos sin procesar en tal forma que forma un arreglo individualmente. Los elementos se representan individualmente en la serie individual. Se utiliza para representar valores numéricos. Por ejemplo, supongamos que los estudiantes de una clase deben obtener las siguientes calificaciones de 100:

56, 77, 88, 49, 60, 92, 70, 81, 69, 51,

Los datos anteriores no son concluyentes sobre cuántos estudiantes obtuvieron 56 puntos o más de 77 en una sola vista.

Serie discreta

La serie discreta se utiliza para reflejar datos para cada valor específico de la variable de observación. Cada una de las variables corresponde a un valor entero. La medida exacta de los elementos en los datos es visible. Por ejemplo, los salarios ganados por 30 trabajadores se muestran a continuación en las tablas como:

Salarios	Número de trabajadores (frecuencia)
2500	7
3000	9
4000	5
4500	6
5000	3

En conclusión, 7 trabajadores reciben salarios equivalentes a Rs. 2500, y 9 trabajadores obtienen Rs. 3000 y así sucesivamente.

Serie continua

Una serie continua contiene elementos de datos mantenidos en ciertas clases definidas. Los elementos de datos contenidos en las clases pierden su identidad individual y los elementos individuales se fusionan en uno u otro grupo de clases. Las clases tienen continuidad, es decir, el final de la primera clase está marcado por el comienzo de la siguiente clase. De ahí el nombre de serie continua. Por ejemplo, la serie continua se representa utilizando los siguientes datos:

Grupo de edad	Frecuencia
10-20	15
20-30	10
30-40	13
40-50	12
50-60	18
60-70	4
70-80	8

Series Individuales

Desviación media (DM) = $\frac{\sum|x-\bar x|}{N}$

Dónde,

∑ – Suma

x – Observación

$\bar x$ – Significar

N – Número de observación

Serie discreta

Desviación media (DM) = $\frac{\sum f|x-\bar x|}{\sum f}$

Dónde,

∑ – Suma

x – Observación

$\bar x$ – Significar

f – frecuencia de observación

Serie continua

Desviación media (DM) = $\frac{\sum f|x-\bar x|}{\sum f}$

Dónde,

∑ – Suma

x – Valor medio de la clase

$\bar x$ – Significar

f – frecuencia de observación

Desviación media de la mediana

Series Individuales

Desviación media (DM) = $\frac{\sum |x-M|}{N}$

Dónde,

∑ – Suma

x – Observación

M – Mediana

N – Número de observación

Serie discreta

Desviación media (DM) = $\frac{\sum f |x-M|}{\sum f}$

Dónde,

∑ – Suma

x – Observación

M – Mediana

N – Frecuencia de las observaciones

Serie continua

Desviación media (DM) = $\frac{\sum f |x-M|}{\sum f}$

Dónde,

∑ – Suma

x – Observación

M – Mediana

N – Frecuencia de las observaciones

Desviación media de la moda

Series Individuales

Desviación media (DM) = $\frac{\sum |x-Mode|}{\sum N}$

Dónde,

∑ – Suma

x – Observación

M-modo

N – Número de observaciones

Serie discreta

Desviación media (DM) = $\frac{\sum f |x-Mode|}{\sum f}$

Dónde,

∑ – Suma

x – Observación

M-modo

N – Frecuencia de las observaciones

Serie continua

Desviación media (DM) = $\frac{\sum f |x-Mode|}{\sum f}$

Dónde,

∑ – Suma

x – Observación

M-modo

N – Frecuencia de las observaciones

Pasos para calcular la desviación media

Calcula la media, la mediana o la moda de la serie.
Calcule las desviaciones de la media, la mediana o la moda e ignore los signos menos.
Multiplique las desviaciones por la frecuencia. El paso se requiere solo en las series discretas y continuas.
Sumar todas las desviaciones.
Aplicar la fórmula.

Ejemplos;

Ejemplo 1: ¿Cuáles son las ventajas de usar la desviación media?

Solución:

Las ventajas de usar la desviación media son:

Se basa en todos los valores de datos proporcionados y, por lo tanto, proporciona una mejor medida de la dispersión.

Es fácil de entender y calcular.

Ejemplo 2: Menciona el procedimiento para encontrar la desviación media.

Solución:

The procedure to find the mean deviation are:

Step 1: Calculate the mean value for the data given.

Step 2: Then, the mean is subtracted from each data value (distance).

Paso 3: Finalmente, se encuentra la media de la distancia.

Ejemplo 3: ¿Encuentra la desviación media de los siguientes datos?

7, 5, 1, 3, 6, 4, 10

Solución:

Para encontrar la desviación media,

Primero, calcule el valor medio de los datos dados

Media = $\frac{suma\ de\ todas\ las\ observaciones}{Número\ de\ observaciones}\\ = \frac{7+ 5+ 1+ 3+ 6+ 4+ 9}{7}\\ =\frac{35 {7}$

Media = 5

Ahora reste la media de cada valor de datos {ignorar negativo (-)}

7 – 5 = 2

5 – 5 = 0

1 – 5 = 4

3 – 5 = 2

6 – 5 = 1

4 – 5 = 1

10 – 5 = 5

Además, encuentre la media de estos valores obtenidos.

2, 0, 4, 2, 1, 1, 5

Media = $\frac{suma\ de\ todas\ las\ observaciones}{Número\ de\ observaciones}\\ = \frac{2+ 0+ 4+ 2+ 1+ 1+ 5}{7}\\ =\frac{15 {7}$

Media = 2,14

Por lo tanto,

La desviación media para 7, 5, 1, 3, 6, 4, 10 es 2,14

Ejemplo 4: ¿Encuentra la desviación media de los siguientes datos?

11, 9, 7, 3, 2, 8, 10, 12, 15, 13

Solución:

Para encontrar la desviación media,

Primero, calcule el valor medio de los datos dados

Media = $\frac{sum\ of\ all\ the\ observations}{Number\ of\ observations}\\ = \frac{11+ 9+ 7+ 3+ 2+ 8+ 10+ 12+ 15+ 13}{10}\\ =\frac{80}{10}$

Media = 8

Ahora reste la media de cada valor de datos {ignorar negativo (-)}

11 – 8 = 3

9 – 8 = 1

7 – 8 = 1

3 – 8 = 5

2 – 8 = 6

8 – 8 = 0

10 – 8 = 2

12 – 8 = 4

15 – 8 = 7

13 – 8 = 5

Además, encuentre la media de estos valores obtenidos.

3, 1, 1, 5, 6, 0, 2, 4, 7, 5.

Media = $\frac{sum\ of\ all\ the\ observations}{Number\ of\ observations}\\ = \frac{3+ 1+ 1+ 5+ 6+ 0+ 2+ 4+ 7+ 5 }{10}\\ =\frac{34}{10}$

Media = 3.4

Por lo tanto,

La desviación media para 11, 9, 7, 3, 2, 8, 10, 12, 15, 13 es 3,4.

Publicación traducida automáticamente

Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Desviación media

Tipos de desviación media

Deja una respuesta Cancelar la respuesta