Aprendizaje de perceptrón multicapa en Tensorflow

En este artículo, comprenderemos el concepto de un perceptrón multicapa y su implementación en Python utilizando la biblioteca TensorFlow.

Perceptrón multicapa 

La percepción multicapa también se conoce como MLP. Se trata de capas densas totalmente conectadas, que transforman cualquier dimensión de entrada en la dimensión deseada. Una percepción multicapa es una red neuronal que tiene múltiples capas. Para crear una red neuronal, combinamos neuronas para que las salidas de algunas neuronas sean entradas de otras neuronas.

Puede encontrar una introducción suave a las redes neuronales y TensorFlow aquí:

• Redes neuronales
• Introducción a TensorFlow

Un perceptrón multicapa tiene una capa de entrada y para cada entrada hay una neurona (o Node), tiene una capa de salida con un solo Node para cada salida y puede tener cualquier cantidad de capas ocultas y cada capa oculta puede tener cualquier número de Nodes. A continuación se muestra un diagrama esquemático de un perceptrón multicapa (MLP).

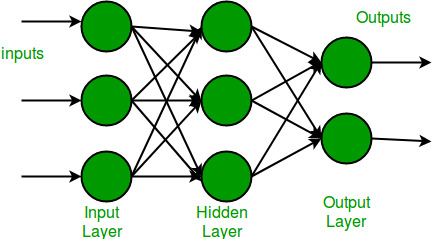
En el diagrama de perceptrón multicapa anterior, podemos ver que hay tres entradas y, por lo tanto, tres Nodes de entrada y la capa oculta tiene tres Nodes. La capa de salida da dos salidas, por lo tanto, hay dos Nodes de salida. Los Nodes en la capa de entrada toman la entrada y la reenvían para su posterior procesamiento, en el diagrama de arriba, los Nodes en la capa de entrada reenvían su salida a cada uno de los tres Nodes en la capa oculta, y de la misma manera, la capa oculta procesa el información y la pasa a la capa de salida. 

Cada Node en la percepción multicapa utiliza una función de activación sigmoidea. La función de activación sigmoidea toma valores reales como entrada y los convierte en números entre 0 y 1 utilizando la fórmula sigmoidea.

Ahora que hemos terminado con la parte teórica de la percepción multicapa, avancemos e implementemos código en python usando la biblioteca TensorFlow .

Implementación paso a paso

Paso 1: importa las bibliotecas necesarias. 

# importing modules
import tensorflow as tf
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Activation
import matplotlib.pyplot as plt

Paso 2: Descarga el conjunto de datos.

TensorFlow nos permite leer el conjunto de datos MNIST y podemos cargarlo directamente en el programa como un conjunto de datos de entrenamiento y prueba.

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

Producción:

Descarga de datos de https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz

11493376/11490434 [==============================] – 2s 0us/paso

Paso 3: Ahora convertiremos los píxeles en valores de coma flotante.

# Cast the records into float values
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
  
# normalize image pixel values by dividing 
# by 255
gray_scale = 255
x_train /= gray_scale
x_test /= gray_scale

Estamos convirtiendo los valores de píxel en valores de punto flotante para hacer las predicciones. Cambiar los números a valores en escala de grises será beneficioso ya que los valores se vuelven pequeños y el cálculo se vuelve más fácil y rápido. Como los valores de píxel van de 0 a 256, aparte de 0, el rango es 255. Entonces, dividir todos los valores por 255 lo convertirá en un rango de 0 a 1

Paso 4: comprender la estructura del conjunto de datos

print("Feature matrix:", x_train.shape)
print("Target matrix:", x_test.shape)
print("Feature matrix:", y_train.shape)
print("Target matrix:", y_test.shape)

Producción:

Feature matrix: (60000, 28, 28)
Target matrix: (10000, 28, 28)
Feature matrix: (60000,)
Target matrix: (10000,)

Por lo tanto, obtenemos que tenemos 60 000 registros en el conjunto de datos de entrenamiento y 10 000 registros en el conjunto de datos de prueba y cada imagen en el conjunto de datos tiene un tamaño de 28 × 28.

Paso 5: Visualiza los datos.

fig, ax = plt.subplots(10, 10)
k = 0
for i in range(10):
    for j in range(10):
        ax[i][j].imshow(x_train[k].reshape(28, 28), 
                        aspect='auto')
        k += 1
plt.show()

Producción

Paso 6: Forme las capas de entrada, ocultas y de salida.

model = Sequential([
    
    # reshape 28 row * 28 column data to 28*28 rows
    Flatten(input_shape=(28, 28)),
    
      # dense layer 1
    Dense(256, activation='sigmoid'),  
    
    # dense layer 2
    Dense(128, activation='sigmoid'), 
    
      # output layer
    Dense(10, activation='sigmoid'),  
])

Algunos puntos importantes a tener en cuenta:

• El modelo secuencial nos permite crear modelos capa por capa según sea necesario en un perceptrón multicapa y está limitado a pilas de capas de una sola entrada y una sola salida.
• Flatten aplana la entrada proporcionada sin afectar el tamaño del lote. Por ejemplo, si las entradas tienen forma (batch_size) sin un eje de función, el aplanamiento agrega una dimensión de canal adicional y la forma de salida es (batch_size, 1).
• La activación es para usar la función de activación sigmoide.
• Las dos primeras capas densas se utilizan para crear un modelo totalmente conectado y son las capas ocultas.
• La última capa densa es la capa de salida que contiene 10 neuronas que deciden a qué categoría pertenece la imagen.

Paso 7: Compile el modelo.

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

Aquí se utiliza la función de compilación que implica el uso de pérdida, optimizadores y métricas. Aquí la función de pérdida utilizada es sparse_categorical_crossentropy , el optimizador utilizado es adam .

Paso 8: ajuste el modelo.

model.fit(x_train, y_train, epochs=10, 
          batch_size=2000, 
          validation_split=0.2)

Producción:

Algunos puntos importantes a tener en cuenta:

• Las épocas nos dicen la cantidad de veces que el modelo será entrenado en pases hacia adelante y hacia atrás.
• El tamaño del lote representa el número de muestras. Si no se especifica, el tamaño del lote será 32 por defecto.
• La división de validación es un valor flotante entre 0 y 1. El modelo separará esta fracción de los datos de entrenamiento para evaluar la pérdida y cualquier métrica del modelo al final de cada época. (El modelo no será entrenado con estos datos)

Paso 9: Encuentre la precisión del modelo.

results = model.evaluate(x_test,  y_test, verbose = 0)
print('test loss, test acc:', results)

Producción:

test loss, test acc: [0.27210235595703125, 0.9223999977111816]

Obtuvimos la precisión de nuestro modelo en un 92 % mediante el uso de model.evaluate() en las muestras de prueba.