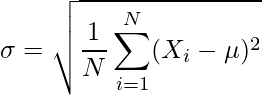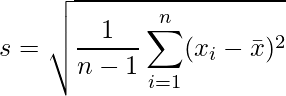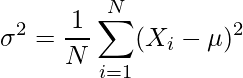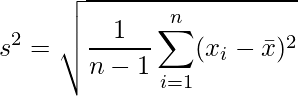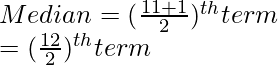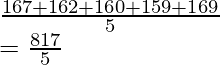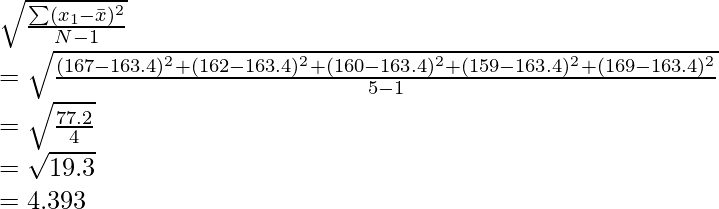¿Cuáles son algunas de las fórmulas importantes que se usan en estadística?

La estadística es una rama de la ciencia que se utiliza para la recopilación, evaluación y resumen de datos. Resume los datos en un formato matemático. Las estadísticas se utilizan principalmente para obtener una comprensión de los datos y centrarse en diversas aplicaciones. Se utiliza para recopilar hechos y cifras sobre el conjunto de datos especificado mediante el conjunto de números. La estadística matemática aplica técnicas matemáticas como álgebra lineal, ecuaciones diferenciales, análisis matemático y teorías de probabilidad.

Hay dos métodos de análisis de datos en estadística matemática que se utilizan a gran escala:

Estadísticas descriptivas
Estadística inferencial

Algunas de las fórmulas importantes utilizadas en estadística

Significar

También conocida como media aritmética, se calcula calculando el promedio de un conjunto dado de números. Es la suma de todos los valores de datos dados dividida por el número total de valores de datos dados en el conjunto. Se calcula de la siguiente forma:

$Mean = \frac{Sum\ of\ Observations}{Total\ number\ of\ observations}$

fórmula media

La media de un conjunto de datos dado se especifica mediante la siguiente fórmula,

$Mean = \frac{Sum\ of\ Observations}{Total\ number\ of\ observations}$

$x̄ = \frac{Σfx}{Σf}$

dónde,

x̄ = el valor medio del conjunto de datos dados.

f = frecuencia de cada clase

x = valor del intervalo medio de cada clase

Por lo tanto, el promedio de todos los puntos de datos se denomina media.

Mediana

La mediana del conjunto dado de números se calcula como la observación más intermedia. Este valor se obtiene después de ordenar los datos en orden ascendente. La mediana de los datos es una medida de la tendencia central de los datos y, por lo tanto, es útil para el análisis de datos. También conocido como Promedio de lugar, la mediana es una métrica fácil de calcular. Son los datos colocados en medio de una secuencia de datos específica.

Fórmula mediana

Para encontrar la mediana del conjunto de datos, primero se ordenan los números en orden ascendente. El valor medio se calcula a partir de lo siguiente.

Número impar de observaciones

En caso de que el número total de observaciones contenidas en el conjunto de datos sea impar, la fórmula de la mediana es la siguiente:

$Median = (\frac{n+1}{2})^{th}term$

donde n es el número de observaciones

número par de observaciones

En caso de que el número total de observaciones contenidas en el conjunto de datos sea par, la fórmula de la mediana es la siguiente:

$Median = \frac{[(\frac{n}{2})^{th} term + ((\frac{n}{2})+1)^{th}term]}{2}$

donde, n es el número de observaciones

Modo

otros conjuntos

Es el valor que aparece más veces.

Por ejemplo, en el conjunto de números dado: 8, 9, 10, 10, 5, 10, la moda del conjunto de datos dado de enteros es 10 ya que ocurre el número máximo de veces, es decir, tres veces.

Fórmula de moda para datos no agrupados

El cálculo de datos no agrupados requiere la disposición de valores de datos en orden ascendente o descendente. Los valores repetidos luego se encuentran y capturan junto con su frecuencia. Ahora, la observación capturada con la frecuencia más alta es el valor modal para los datos dados. Este es el valor modal calculado.

Fórmula de moda para datos agrupados

$Mode = I_0 + \left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)h$

En esta fórmula tenemos,

I ₀ es el límite inferior de la clase modal

h es el tamaño del intervalo de clase

f ₁ es la frecuencia de la clase modal

f ₀ es la frecuencia de la clase que precede a la clase modal

f ₂ es la frecuencia de la clase que sucede a la clase modal

Desviación Estándar

La desviación estándar es una medida del grado de dispersión de los valores que forman el conjunto de datos. Es la medida de la dispersión relativa a su valor correspondiente.

Fórmula de desviación estándar

Desviación estándar de población

$\displaystyle\sigma=\sqrt{\frac{1}{N}\sum^N_{i=1}(X_i-\mu)^2}$

En esta fórmula tenemos,

σ = Desviación estándar de la población

N = Número de observaciones en la población

X _i = i ^-ésima observación en la población

μ = Media de la población

Desviación estándar de la muestra

$\displaystyle s=\sqrt{\frac{1}{n-1}\sum^n_{i=1}(x_i-\bar x)^2}$

En esta fórmula tenemos,

s = desviación estándar de la muestra

n = Número de observaciones en la muestra

x _i = i ^-ésima observación en la muestra

$\bar x$ = Media muestral

Diferencia

La varianza de la distribución de datos es una medida de cómo los puntos de datos difieren de la media. Es un indicador de la medida de cuánto se separa un conjunto de números de su valor promedio correspondiente. Se considera que la varianza de los datos es el doble de la desviación estándar.

Se utiliza para calcular la diferencia esperada de desviación del valor real. La varianza depende de la desviación estándar del conjunto de datos especificado de las observaciones. Esto implica que si la varianza es mayor, los valores de los datos están más separados de la media y, de manera similar, si la varianza es menor, los valores de los datos están menos separados de la media. Por lo tanto, mide la dispersión de datos de la media del conjunto de datos.

Fórmula de varianza

Varianza de la población

$\displaystyle\sigma^2=\frac{1}{N}\sum^N_{i=1}(X_i-\mu)^2$

En esta fórmula tenemos,

σ = Desviación estándar de la población

N = Número de observaciones en la población

X _i = i ^-ésima observación en la población

μ = Media de la población

Varianza de la muestra

$\displaystyle s^2=\sqrt{\frac{1}{n-1}\sum^n_{i=1}(x_i-\bar x)^2}$

En esta fórmula tenemos,

s = desviación estándar de la muestra

n = Número de observaciones en la muestra

x _i = i ^-ésima observación en la muestra

$\bar x$ = Media muestral

Ejemplos de preguntas

Pregunta 1. Encuentra la media de las calificaciones de las pruebas de clase de 10 estudiantes de 100

99, 95, 87, 55, 72, 86, 92, 89, 75, 88

Solución:

Para encontrar la media de los datos primero necesitamos encontrar la suma de todas las calificaciones de los estudiantes

Suma de observaciones = 99+95+87+55+72+86+92+89+75+88 = 838

Número de observaciones = 10

Por lo tanto,

$Mean = \frac{Sum\ of\ Observations}{Total\ number\ of\ observations} \\ =\frac{838}{10}$

= 83,8

Por lo tanto,

La media de las notas de 10 alumnos es 83,8

Pregunta 2. Encuentra la mediana de los siguientes datos

2, 45, 15, 18, 11, 85, 19, 22, 7, 5, 13

Solución:

Primero organice estos datos en orden ascendente

2, 5, 7, 11, 13, 15, 18, 19, 22, 45, 85

Aquí como podemos ver que el número de observación es 11 que es impar.

Por lo tanto, aplique la fórmula de la mediana cuando el número de observaciones sea impar.

$Median = (\frac{n+1}{2})^{th}term$

Aquí n = número de observación que es 11, n = 11

$Median = (\frac{11+1}{2})^{th}term\\ =(\frac{12}{2})^{th}term$

Mediana = 6 ^° término

Eso es 15

Por lo tanto,

La mediana de los datos es 15.

Pregunta 3. Encuentra la moda de las calificaciones obtenidas por los estudiantes en la prueba de clase de 50 para 40 estudiantes

Marcas obtenidas	Numero de estudiantes
10-20	4
20-30	8
30-40	dieciséis
40-50	12

Solución:

Para encontrar la moda usa la fórmula de la moda para datos agrupados

$Mode = I_0 + \left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)h$

Aquí tenemos,

f ₁ = La frecuencia de clase máxima = 16

El intervalo de clase de f ₁ = 30-40

l ₀ = Límite inferior de la frecuencia máxima (clase modal) = 30

h = Tamaño del intervalo de clase = 10

f ₀ = Frecuencia de la clase precedente = 8

f ₂ = Frecuencia de la clase siguiente = 12

Ahora ponga todos estos valores en la fórmula de modo para datos agrupados

$Mode = I_0 + \left(\frac{f_1-f_0}{2f_1-f_0-f_2}\right)h\\ =30+\frac{16-8}{2\times16-8-12}\times10\\ =30+\frac{8}{12}\times10\\ =30+\frac{80}{12}$

= 30+ 6.66

= 36,66

Por lo tanto,

Moda = 36,66

Pregunta 4. Suponga que hay 40 estudiantes en una clase. Se seleccionaron al azar 5 estudiantes y sus alturas se midieron como 167, 162, 160, 159, 169. ¿Calcula la desviación estándar de sus alturas?

Solución:

Aquí,

norte = 5

Media $(\bar x)$ = $\frac{167+ 162+ 160+ 159+ 169}{5}\\ =\frac{817}{5}$

$(\bar x)$ = 163,4

Desviación estándar (DE) = $\sqrt{\frac{\sum(x_1-\bar x)^2}{N-1}}\\ =\sqrt{\frac{(167-163.4)^2+(162-163.4)^2+(160-163.4)^2+(159-163.4)^2+(169-163.4)^2 }{5-1}}\\ =\sqrt{\frac{77.2}{4}}\\ =\sqrt{19.3}\\ =4.393$

Desviación Estándar = 4.393

Pregunta 5. En el ejemplo anterior, ¿encontrar la varianza de las alturas de los 5 estudiantes seleccionados?

Solución:

Como sabemos que,

Varianza = SD ²

Desviación Estándar = 4.393

Varianza = 4.393 ²

Varianza = 19.298

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Algunas de las fórmulas importantes utilizadas en estadística

Fórmula de desviación estándar

Fórmula de varianza

Ejemplos de preguntas

Deja una respuesta Cancelar la respuesta