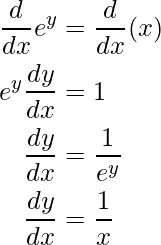En el artículo anterior, hemos discutido la parte de introducción y algunos ejemplos básicos de diferenciación implícita . Entonces, en este artículo, discutiremos algunos ejemplos avanzados de diferenciación implícita.
Diferenciación implícita
La diferenciación implícita es un método que utiliza la regla de la string para diferenciar funciones implícitamente definidas. Por lo general, no es fácil encontrar la función explícitamente y luego diferenciarla. En cambio, podemos derivar totalmente f(x, y) y luego resolver el resto de la ecuación para encontrar el valor de ![]() . Incluso cuando es posible resolver explícitamente la ecuación original, la fórmula resultante de la diferenciación total es, en general, mucho más simple y fácil de usar.
. Incluso cuando es posible resolver explícitamente la ecuación original, la fórmula resultante de la diferenciación total es, en general, mucho más simple y fácil de usar.
Método para resolver
- Derive ambos lados de la ecuación con respecto a x.
- Sigue las reglas de diferenciación.
- Usa la regla de la string para diferenciar expresiones que involucran y.
- Resuelva la ecuación para
Ejemplos avanzados
Ejemplo 1: ¿Encontrar la derivada de y = cos(5x – 3y)?
Solución:
Ecuación dada:
y = cos(5x – 3y)
Paso 1: Diferenciando ambos lados con x,
Paso 2: Usar la regla de la string
Paso 3: Expandiendo la ecuación anterior
Paso 4: Tomando todos los términos con dy/dx en LHS
Paso 5: Tomando dy/dx común de la LHS de la ecuación
Paso 6: Aislar dy/dx
Ejemplo 2: ¿Encontrar la derivada de (x² + y²)³ = 5x²y²?
Solución:
Ecuación dada:
(x² + y²)³ = 5x²y²
Ejemplo 3: Encuentra la derivada de ![]() ?
?
Solución:
Ecuación dada:
Ejemplo 4: ¿Encontrar la derivada de y = ln(x)?
Solución:
Ecuación dada:
y = ln(x)
=> e y = x
Publicación traducida automáticamente
Artículo escrito por rathoreatul27 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA