Los hiperparámetros son aquellos parámetros que establecemos para el entrenamiento. Los hiperparámetros tienen un gran impacto en la precisión y la eficiencia al entrenar el modelo. Por lo tanto, era necesario configurarlo con precisión para obtener resultados mejores y más eficientes. Primero analicemos algunos métodos de búsqueda exhaustiva para optimizar el hiperparámetro.
Métodos de búsqueda exhaustivos
Grid Search: En Grid Search, los posibles valores de los hiperparámetros se definen en el conjunto. Luego, estos conjuntos de posibles valores de hiperparámetros se combinan mediante el uso del producto cartesiano y forman una cuadrícula multidimensional. Luego probamos todos los parámetros en la cuadrícula y seleccionamos la configuración de hiperparámetro con el mejor resultado. Búsqueda aleatoria: esta es otra variante de la búsqueda en cuadrícula en la que, en lugar de probar todos los puntos de la cuadrícula, probamos puntos aleatorios. Esto resuelve un par de problemas que se encuentran en Grid Search, como que no necesitamos expandir nuestro espacio de búsqueda exponencialmente cada vez que agregamos un nuevo hiperparámetro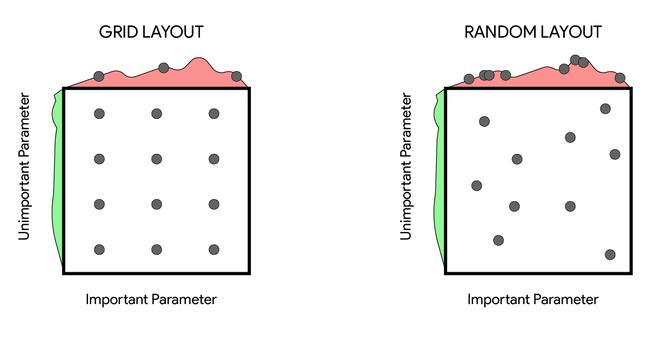
Retirarse:
La búsqueda aleatoria y la búsqueda en cuadrícula son fáciles de implementar y pueden ejecutarse en paralelo, pero aquí hay algunos inconvenientes de estos algoritmos:
- Si el espacio de búsqueda de hiperparámetros es grande, se necesita mucho tiempo y potencia de cálculo para optimizar el hiperparámetro.
- No hay garantía de que estos algoritmos encuentren máximos locales si la muestra no se realiza meticulosamente.
Optimización bayesiana:
En lugar de adivinar al azar, en la optimización bayesiana usamos nuestro conocimiento previo para adivinar el hiperparámetro. Usan estos resultados
![]()
Esta función también se llama «sustituto» de la función objetivo. Es mucho más fácil de optimizar que la función Objetivo. A continuación se muestran los pasos para aplicar la optimización bayesiana para la optimización de hiperparámetros:
- Construir un modelo de probabilidad sustituto de la función objetivo
- Encuentre los hiperparámetros que funcionan mejor en el sustituto
- Aplique estos hiperparámetros a la función objetivo original
- Actualice el modelo sustituto utilizando los nuevos resultados
- Repita los pasos 2 a 4 hasta el número n de iteraciones
Optimización basada en modelos secuenciales:
La optimización basada en modelos secuenciales (SMBO) es un método para aplicar la optimización bayesiana. Aquí secuencial se refiere a ejecutar ensayos uno tras otro, cada vez mejorando los hiperparámetros mediante la aplicación del modelo de probabilidad bayesiano (sustituto).
Hay 5 parámetros importantes de SMBO:
- Dominio del hiperparámetro sobre el cual .
- Una función objetivo que genera una puntuación que queremos optimizar.
- Una distribución sustituta de la función objetivo
- Una función de selección para seleccionar qué hiperparámetro elegir a continuación. Por lo general, tomamos en cuenta la mejora esperada
- Una estructura de datos contiene el historial de pares anteriores (puntuación, hiperparámetro) que se utilizan en iteraciones anteriores.
Hay muchas versiones diferentes del algoritmo de optimización de hiperparámetro SMBO. Esta diferencia común entre ellos son las funciones sustitutas. Algunas funciones sustitutas, como el proceso gaussiano, la regresión aleatoria de bosques, el estimador Tree Prazen. En esta publicación, discutiremos Tree Prazen Estimator a continuación.
Estimadores de Tree Prazen:
Tree Prazen Estimators utiliza una estructura de árbol para optimizar el hiperparámetro. Muchos hiperprametros se pueden optimizar utilizando este método, como el número de capas, el optimizador en el modelo, el número de neuronas en cada capa. En el estimador de árbol prazen en lugar de calcular P(y | x ) calculamos P(x|y) y P(y) (donde y es una puntuación intermedia que decide qué tan buenos son los valores de este hiperparámetro, como la pérdida de validación y x es hiperparámetro).
En el primero de Tree Prazen Estimator, muestreamos la pérdida de validación mediante una búsqueda aleatoria para inicializar el algoritmo. Luego dividimos las observaciones en dos grupos: la de mejor desempeño (por ejemplo, el cuartil superior) y el resto, tomando y* como el valor de división para los dos grupos.
Luego calculamos la probabilidad de que el hiperparámetro esté en cada uno de estos grupos, como
P(x|y) = f(x) si y<y* y p(x|y) = g(x) si y?y*.
Las dos densidades y g se modelan utilizando estimadores de Parzen (también conocidos como estimadores de densidad kernel) que son un promedio simple de kernels centrados en puntos de datos existentes.
P(y) se calcula usando el hecho de que p(y<y*)=? que define la división de percentiles en las dos categorías.
Utilizando la regla de Baye (es decir, p(x, y) = p(y) p(x|y) ), se puede demostrar que la definición de mejoras esperadas es equivalente a f(x)/g(x).
En este paso final tratamos de maximizar f(x)/g(x)
Retirarse:
La mayor desventaja de Tree Prazen Estimator es que selecciona hiperparámetros independientemente unos de otros, lo que de alguna manera afecta la eficiencia y el cálculo requerido porque en la mayoría de las redes neuronales existen relaciones entre diferentes hiperparámetros.
Otros algoritmos de estimación de hiperparámetros:
Hiperbanda
El principio subyacente de este algoritmo es
- Muestra aleatoriamente n número de conjuntos de hiperparámetros en el espacio de búsqueda.
- Después de k iteraciones, evalúe la pérdida de validación de estos hiperpametros.
- Deseche la mitad de los hiperparámetros de menor rendimiento.
- Ejecute los buenos para k iteraciones más y evalúe y descarte la mitad inferior.
- Repita hasta que solo nos quede un modelo de hiperparámetro.
Inconvenientes:
- Si el número de muestras es grande, algunos conjuntos de hiperparámetros de buen rendimiento que requirieron algo de tiempo para converger pueden descartarse al principio de la optimización.
Formación basada en la población (PBT):
El entrenamiento basado en la población (PBT) comienza de manera similar al entrenamiento aleatorio al entrenar muchos modelos en paralelo. Pero en lugar de que las redes se entrenen de forma independiente, utiliza información del resto de la población para refinar los hiperparámetros y dirigir los recursos computacionales a modelos que se muestran prometedores. Esto se inspira en los algoritmos genéticos en los que cada miembro de la población, denominado trabajador, puede explotar la información del resto de la población. por ejemplo, un trabajador podría copiar los parámetros del modelo de un trabajador mucho mejor. También puede explorar nuevos hiperparámetros cambiando los valores actuales aleatoriamente.
(BOHB):
BOHB (optimización bayesiana e hiperbanda) es una combinación del algoritmo hiperbanda y la optimización bayesiana. En primer lugar, utiliza la capacidad de hiperbanda para muestrear muchas configuraciones con un presupuesto pequeño para explorar de manera rápida y eficiente el espacio de búsqueda de hiperparámetros y obtener muy pronto configuraciones prometedoras, luego utiliza la capacidad predictiva del optimizador bayesiano para proponer un conjunto de hiperparámetros que están cerca del óptimo. .Este algoritmo también se puede ejecutar en paralelo (como Hyperband), lo que supera un gran inconveniente de la optimización bayesiana.
Referencias: