La correlación es una herramienta estadística que se utiliza para analizar y medir el grado de relación o grado de asociación entre dos o más variables. Generalmente hay tres tipos de correlación:
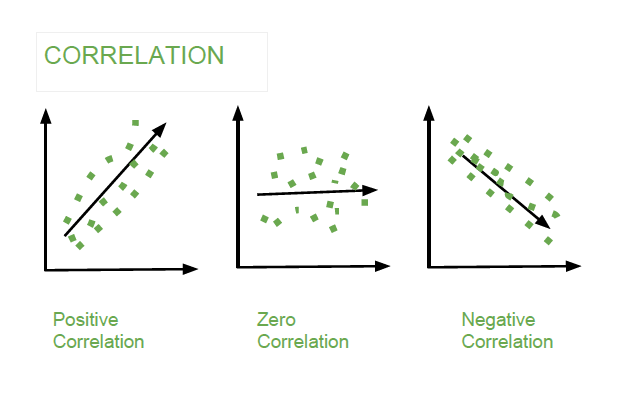
- Correlación positiva : Cuando aumentamos el valor de una variable, el valor de otra variable aumenta respectivamente, esto se llama Correlación Positiva.
- Correlación negativa : Cuando aumentamos el valor de una variable, el valor de otra variable disminuye respectivamente, esto se llama Correlación negativa.
- Correlación cero : cuando el cambio en el valor de una variable no afecta sustancialmente a otra, se denomina correlación cero.
Correlación de Pearson:
La correlación de Pearson es la forma más común de calcular la correlación. Se denota por r. Considere para dos variables x e y, está representado por la siguiente fórmula:
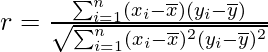
Un valor más cercano a -1 representa una correlación perfectamente negativa, mientras que 0 representa ninguna correlación y 1 representa una fuerte correlación positiva.
El coeficiente de correlación de Pearson es un buen estimador de correlación entre dos variables para una distribución normal. Sin embargo, no cumple con los criterios del estimador robusto porque no es:
- Resistente : esto significa que cambiar una pequeña fracción de datos, incluso por una gran cantidad, no afecta considerablemente el valor de la estimación.
- Robustez de la eficiencia : la estadística tiene una alta eficiencia en una variedad de situaciones en lugar de en una sola situación. Eficiencia significa que la estimación está cerca de la estimación óptima dado que sabemos de qué distribución provienen los datos.
La eficiencia se puede medir utilizando la siguiente fórmula:
![]()
Correlación de curvatura porcentual:
Shoemaker y Hettmanspergr propusieron la correlación de porcentaje de flexión en 1982 y también la mencionó Wilcox en su libro. Esta correlación es a la vez resistente y robusta a la eficiencia.
Los siguientes son los pasos para realizar la correlación de desviación porcentual en dos variables X e Y:
- Establezca m = (1-\beta) *m + 0.5, redondee m al entero más cercano. Aquí, \beta está entre 0 y 0,5
- Tome W_{i} = |X_{i} – M_{x}| para i = 1, 2, …n, donde M_x es la mediana de X.
- Ordene W_i en orden ascendente.
 , donde W(m) es la estimación del cuantil (1-\beta) de W.
, donde W(m) es la estimación del cuantil (1-\beta) de W.- Ordenar los valores de X.
- Calcular el número de valores \frac{(X_{i} – M_{x})}{\hat{W}_{x}(\beta)} que son <-1 y almacenar en i_1 y el número que son > +1 y almacenar en
 respectivamente. Luego calcula lo siguiente:
respectivamente. Luego calcula lo siguiente:
![]()
![]()
![]()
- Repita los pasos anteriores para que el estimador Y obtenga \hat{W_y}, \hat{\phi}_{y} y V_i.
- Defina la función:
![]()
por lo tanto calcula,
![]()
- Calcule la correlación porcentual de curvatura:

Correlación Winsorizada:
La correlación estándar como Pearson a veces está fuertemente influenciada por valores extremos. La correlación Winsorizada resuelve esto al establecer los valores de la cola igual a un cierto valor de percentil.
Por ejemplo, para una correlación Winsorizada del 90 %, el 5 % inferior de los valores se establece igual al valor correspondiente al percentil 5, mientras que el 5 % superior de los valores se establece igual al valor correspondiente al percentil 95. Luego se aplica la correlación estándar.
Implementación:
- En esta implementación, usaremos el conjunto de datos Motor Trend Car Road Tests disponible en la biblioteca de gráficos en R. Es muy popular y está fácilmente disponible. Este conjunto de datos contiene 32 observaciones de 11 variables diferentes relacionadas con los automóviles. Realizaremos el análisis de correlación entre estas variables (Pearson, porcentaje de curvatura y winsorizado) y las graficaremos.
R
# Install the required packages
install.packages("dplyr")
install.packages("correlation")
install.packages("see")
# import required packages
library(dplyr)
library(correlation)
library(see)
# Load data
data("mtcars")
# check help for mtcars data
?mtcars
## Description
# The data was extracted from the 1974 Motor Trend US magazine,
# and comprises fuel consumption and 10 aspects of automobile
# design and performance for 32 automobiles
#(1973–74 models).
## Usage
# mtcars
## Format
# A data frame with 32 observations on 11 (numeric) variables.
#
# [, 1] mpg Miles/(US) gallon
# [, 2] cyl Number of cylinders
# [, 3] disp Displacement (cu.in.)
# [, 4] hp Gross horsepower
# [, 5] dart Rear axle ratio
# [, 6] wt Weight (1000 lbs)
# [, 7] qsec 1/4 mile time
# [, 8] vs Engine (0 = V-shaped, 1 = straight)
# [, 9] am Transmission (0 = automatic, 1 = manual)
# [,10] gear Number of forward gears
# [,11] carb Number of carburetors
## Source
# Henderson and Velleman (1981), Building multiple regression
# models interactively. Biometrics, 37, 391–411.
# perform different correlation and print summary
# pearson correlation
pearson_corr = correlation(mtcars)
pearson_summary = summary(pearson_corr)
print(pearson_summary)
# percentage bend correlation
pbc_corr = correlation(mtcars,method='percentage')
pbc_summary= summary(pbc_corr)
print(pbc_summary)
# winsorized correlation
wins_corr = correlation(mtcars, winsorize = 0.2)
winsor_summary = summary(wins_corr)
print(winsor_summary)
# plot different correlation analysis
pearson_summary%>%plot()
pbc_summary%>%plot()
winsor_summary%>%plot()
# Correlation Matrix (pearson-method) Parameter | carb | gear | am | vs | qsec | wt | dart | hp | disp | cyl --------------------------------------------------------------------------------------------------------------------- mpg | -0.55* | 0.48 | 0.60** | 0.66** | 0.42 | -0.87*** | 0.68*** | -0.78*** | -0.85*** | -0.85*** cyl | 0.53* | -0.49 | -0.52* | -0.81*** | -0.59* | 0.78*** | -0.70*** | 0.83*** | 0.90*** | disp | 0.39 | -0.56* | -0.59* | -0.71*** | -0.43 | 0.89*** | -0.71*** | 0.79*** | | hp | 0.75*** | -0.13 | -0.24 | -0.72*** | -0.71*** | 0.66** | -0.45 | | | dart | -0.09 | 0.70*** | 0.71*** | 0.44 | 0.09 | -0.71*** | | | | wt | 0.43 | -0.58* | -0.69*** | -0.55* | -0.17 | | | | | qsec | -0.66** | -0.21 | -0.23 | 0.74*** | | | | | | vs | -0.57* | 0.21 | 0.17 | | | | | | | am | 0.06 | 0.79*** | | | | | | | | gear | 0.27 | | | | | | | | | p-value adjustment method: Holm (1979)>
# Correlation Matrix (percentage-method) Parameter | carb | gear | am | vs | qsec | wt | dart | hp | disp | cyl ---------------------------------------------------------------------------------------------------------------------- mpg | -0.64** | 0.55* | 0.58** | 0.68*** | 0.48 | -0.90*** | 0.68*** | -0.90*** | -0.88*** | -0.91*** cyl | 0.58* | -0.55* | -0.52* | -0.81*** | -0.60** | 0.85*** | -0.72*** | 0.91*** | 0.94*** | disp | 0.47 | -0.61** | -0.60** | -0.73*** | -0.50 | 0.88*** | -0.74*** | 0.89*** | | hp | 0.70*** | -0.37 | -0.40 | -0.79*** | -0.69*** | 0.80*** | -0.59** | | | dart | -0.11 | 0.78*** | 0.73*** | 0.47 | 0.13 | -0.76*** | | | | wt | 0.53* | -0.64** | -0.76*** | -0.57* | -0.26 | | | | | qsec | -0.68*** | -0.13 | -0.17 | 0.80*** | | | | | | vs | -0.62** | 0.27 | 0.17 | | | | | | | am | -0.07 | 0.80*** | | | | | | | | gear | 0.11 | | | | | | | | | p-value adjustment method: Holm (1979)>
# Winsorized Correlation Matrix Parameter | carb | gear | am | vs | qsec | wt | dart | hp | disp | cyl --------------------------------------------------------------------------------------------------------------------- mpg | -0.63** | 0.65** | 0.55* | 0.70*** | 0.49 | -0.86*** | 0.67*** | -0.88*** | -0.87*** | -0.93*** cyl | 0.60** | -0.68*** | -0.52* | -0.81*** | -0.60** | 0.87*** | -0.74*** | 0.90*** | 0.94*** | disp | 0.45 | -0.74*** | -0.57* | -0.72*** | -0.51* | 0.85*** | -0.74*** | 0.89*** | | hp | 0.69*** | -0.56* | -0.37 | -0.79*** | -0.63** | 0.77*** | -0.60** | | | dart | -0.12 | 0.88*** | 0.72*** | 0.50* | 0.22 | -0.76*** | | | | wt | 0.53* | -0.69*** | -0.78*** | -0.56* | -0.29 | | | | | qsec | -0.61** | 0.15 | -0.12 | 0.84*** | | | | | | vs | -0.62** | 0.45 | 0.17 | | | | | | | am | -0.11 | 0.78*** | | | | | | | | gear | -0.03 | | | | | | | | | p-value adjustment method: Holm (1979)

Correlación de Pearson

Correlación de curvatura porcentual

Correlación de Winsor