Proyecciones ortogonales

Conjuntos ortogonales:

Un conjunto de vectores $\left \{ u_1, u_2, ... u_p \right \}$ en $\mathbb{R^n}$ se llama conjunto ortogonal, si $u_i \cdot u_j =0$ . si $i \neq j$

Base ortogonal

Una base ortogonal para un subespacio W de $\mathbb{R^n}$ es una base para W que también es un conjunto ortogonal.

Sea S = $\left \{ u_1, u_2, ... u_p \right \}$ la base ortogonal de un W de $\mathbb{R^n}$ es una base de W que también es un conjunto ortogonal. Necesitamos calcular $c_1, c_2, ... c_p$ tal que:

$y = c_1 u_1 + c_2 u_2 + ... c_p u_p$

Tomemos el producto escalar de u_1 en ambos lados.

$y \cdot u_1 = (c_1 u_1 + c_2 u_2 + ... c_p u_p) \cdot u_1$

$y \cdot u_1 = c_1 (u_1 \cdot u_1) + c_2 (u_2 \cdot u_1) + ... c_p (u_p \cdot u_1)$

Ya que, esta es una base ortogonal $u_2 \cdot u_1 = u_3 \cdot u_1 = ... = u_p \cdot u_1 =0$ . Esto da $c_1$ :

$c_1 = \frac{y \cdot u_1}{ u_1 \cdot u_1}$

Podemos generalizar la ecuación anterior

$c_j = \frac{y \cdot u_j}{ u_j \cdot u_j}$

Supongamos que {u_1, u_2,… u_n} es una base ortogonal para W en $\mathbb{R^n}$ . Para cada y en W:

$y =\left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + ... + \left ( \frac{y \cdot u_p}{u_p \cdot u_p } \right )u_p$

Tomemos $\left \{ u_1, u_2, u_3 \right \}$ es una base ortogonal para $\mathbb{R^3}$ y W = span $\left \{ u_1, u_2 \right \}$ . Intentemos escribir una escritura y en la forma $\hat{y}$ que pertenece al espacio W, y z que es ortogonal a W.

$y =\left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + \left ( \frac{y \cdot u_2}{u_2\cdot u_2 } \right )u_2 + \left ( \frac{y \cdot u_3}{u_3 \cdot u_3} \right ) u_3 \\$

dónde

$\hat{y} = \left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + \left ( \frac{y \cdot u_2}{u_2\cdot u_2 } \right )u_2$

$z = \left ( \frac{y \cdot u_3}{u_3 \cdot u_3} \right ) u_3$ [Tex]y= \hat{y} + z[/Tex]

Ahora, podemos ver que z es ortogonal a ambos $u_1$ y $u_2$ tal que:

$z \cdot u_1 =0 \\ z \cdot u_2 =0$

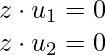
Teorema de descomposición ortogonal:

Sea W el subespacio de $\mathbb{R^n}$ . Entonces cada y en $\mathbb{R^n}$ se puede representar de forma única en la forma:

$y = \hat{y} + z$

donde $\hat{y}$ está en W y z en W^{\perp}. Si $\left \{ u_1, u_2, ... u_p \right \}$ es una base ortogonal de W. entonces,

$\hat{y} =\left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + ... + \left ( \frac{y \cdot u_p}{u_p \cdot u_p } \right )u_p$

de este modo:

$z = y - \hat{y}$

Entonces, $\hat{y}$ es la proyección ortogonal de y en W.

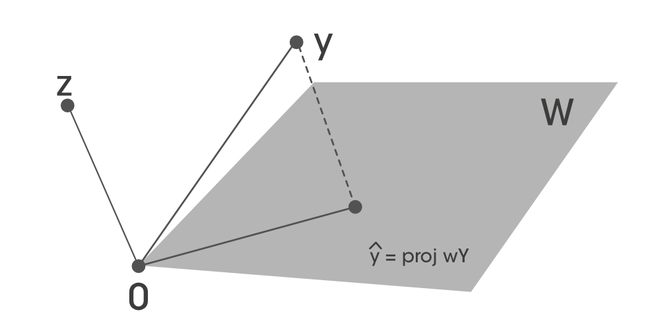
Teorema de la mejor aproximación

Sea W el subespacio de $\mathbb{R^n}$ , y cualquier vector en $\mathbb{R^n}$ . Sea v en W y diferente de $\hat{y}$ . Luego $\left \| v-\hat{y} \right \|$ también en W.