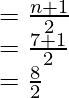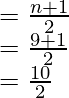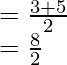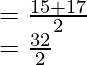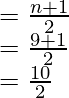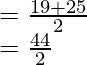¿Qué es un diagrama de caja?

El diagrama de caja es básicamente una escala de intervalo que se utiliza para realizar estimaciones que necesariamente realizan la abstracción de los datos. Los diagramas de caja se utilizan para interpretar y analizar los datos. También se puede utilizar para visualizar los datos. Boxplot es una variación del método gráfico que se utiliza para ilustrar la variación de los datos en la distribución de datos. También se puede utilizar un histograma para mostrar los datos. Sin embargo, si comparamos un diagrama de caja y un histograma, este último ofrece una visualización suficiente. También proporciona información adicional correspondiente a los múltiples conjuntos de datos que se muestran en el mismo gráfico. 

Los diagramas de caja se pueden utilizar necesariamente en situaciones en las que:

• Forma de distribución
• Valor Central
• Variabilidad

Al trazar un gráfico para el diagrama de caja, se delinea una caja que comienza desde el primer cuartil hasta el tercer cuartil. Una línea vertical que atraviesa este cuadro trazado corresponde a la mediana de la distribución de datos. Las pequeñas líneas, llamadas bigotes, van desde cada uno de los cuartiles hacia el valor mínimo o máximo. Este concepto se muestra en la siguiente figura: 

Características del diagrama de caja

• Muestra datos de un resumen de cinco números, que también incluye una de las medidas de tendencia central. Esto implica que tiene cinco piezas de información.
• Particularmente utilizado para reflejar si el conjunto de datos dado es una distribución sesgada o no.
• También proporciona una idea del conjunto de datos, si existe una posible observación inusual. Estos se llaman valores atípicos.
• Refleja información sobre cómo se distribuyen los datos.
• En este caso, las disposiciones pueden combinarse entre sí. Esto se debe a que el centro, la dispersión y el rango general son evidentes al instante en el caso de un diagrama de caja.
• Es particularmente útil para la interpretación de datos descriptivos.
• También se utiliza cuando se trata o se compara un gran número de recopilaciones de datos.

Elementos de un diagrama de caja y bigotes

Los elementos necesarios para construir un diagrama de caja y bigotes de valores atípicos se dan a continuación:

Valor mínimo (Q ₀ o percentil 0): el valor mínimo especificado en la distribución del conjunto de datos dado, que se muestra en el extremo izquierdo.

Primer cuartil (Q ₁ o percentil 25): El primer cuartil (Q ₁ ) del lado izquierdo, que corresponde al área entre el valor mínimo y la mediana.

Mediana (Q ₂ o percentil 50): El valor de la mediana, representado por la línea correspondiente al centro de la caja.

Tercer cuartil (Q ₃ o percentil 75): El tercer cuartil (Q ₃ ) del lado derecho, que corresponde al área entre la mediana y el valor máximo.

Valor máximo (Q ₄ o percentil 100): el valor máximo especificado en la distribución del conjunto de datos dado, que se muestra en el extremo derecho.

Rango intercuartílico: El rango intercuartílico (RIC) es la diferencia entre los cuartiles superior e inferior, es decir, Q ₃ y Q ₁ .

¿Construir un diagrama de caja?

El diagrama de caja y bigotes se puede construir siguiendo los siguientes pasos: 

1. El valor más pequeño en el conjunto de datos especificado se conoce como el valor mínimo.
2. El valor que corresponde por debajo del 25% inferior de los datos contenidos. Se llama el primer cuartil.
3. El tercer valor corresponde a la mediana de los datos dados.
4. El valor que corresponde por encima del 25% inferior de los datos contenidos. Se llama el tercer cuartil.
5. El valor más grande en el conjunto de datos especificado se conoce como el valor máximo.

Aplicaciones

El diagrama de caja se puede utilizar para conocer los siguientes componentes: 

• Los valores atípicos y sus valores.
• Agrupación estrecha de datos
• Simetría de datos
• asimetría de datos

Ejemplos de preguntas

Pregunta 1. Calcular el 

• Valor máximo, 
• Valor mínimo, 
• Mediana, 
• primer cuartil, 
• tercer cuartil 

A partir de estos datos dados: 

2, 7, 19, 12, 23, 15, 26.

Solución:  

Primero organice estos datos en orden ascendente.

2, 7, 12, 15, 19, 23, 26 

Por lo tanto aquí,

• Valor mínimo = 2
• Valor máximo = 26
• Mediana = 
  Mediana = 4 ^° término = 15
• Primer cuartil = valor medio de 2, 7, 19
  Eso es 7
  Por lo tanto, primer cuartil = 7
• Tercer cuartil = valor medio de 19, 23, 26 
  Eso es 23
  Por lo tanto, tercer cuartil = 23

Pregunta 2. Dibuja el diagrama de caja para los datos dados: 

2, 17, 20, 5, 3, 13, 15, 9, 11

Solución:

Primero organice estos datos en orden ascendente

2, 3, 5, 9, 11, 13, 15, 17, 20

Encuentre el rango de los datos

Rango = Valor máximo en este dato – Valor mínimo en este dato

Rango = 20 – 2 = 18

Ahora, 

Encuentra la mediana 

mediana = 

Mediana = ^5to término

mediana = 11

Más lejos, 

Encuentra los cuartiles.

Encontrar el primer cuartil (Q ₁ ) = El primer cuartil (Q ₁ ) en el lado izquierdo, que está entre el valor mínimo y la mediana.

Q ₁ = Mediana de (2, 3, 5, 9)

Q ₁ = 

Q ₁ = 4

Ahora,

Encontrar el tercer cuartil (Q ₃ ) = El tercer cuartil (Q ₃ ) en el lado derecho, que está entre la mediana y el valor máximo.

Q ₃ = Mediana de (13, 15, 17, 20)

Q ₃ = 

Q ₃ = 16

De este modo, 

Encontrar el rango intercuartílico;

Intercuartil = Q ₃ – Q ₁ = 16 – 4 = 12

Por lo tanto, el resumen de cinco números se puede mostrar como:

Valor mínimo, Primer cuartil Q ₁ , Mediana, Tercer cuartil Q ₃ , Valor máximo

Por lo tanto, 

2, 4, 11, 16, 20

Por lo tanto, este es el resumen de cinco números de los datos dados.

Por eso,

Se puede dibujar un diagrama de caja

Pregunta 3. Mencione las ventajas de Box Plot

Solución:

El diagrama de caja y bigotes tiene las siguientes ventajas: 

Fácil identificación de la ubicación de los datos y la distribución de los datos.

Información sobre la asimetría y simetría de los datos.

Información sobre los datos atípicos. 

Pregunta 4. Mencione las desventajas de Box Plot

Solución: 

El diagrama de caja y bigotes tiene las siguientes desventajas: 

La media no se puede localizar fácilmente.

Generalmente oculta la multimodalidad y otras características de determinadas distribuciones.

Pregunta 5. Calcular el

• Valor máximo,
• Valor mínimo,
• Mediana,
• primer cuartil,
• tercer cuartil

A partir de estos datos dados:

5, 7, 2, 19, 25, 18, 26, 9, 11.

Solución: 

Primero organice estos datos en orden ascendente.

2, 5, 7, 9, 11, 18, 19, 25, 26

Por lo tanto aquí,

Valor mínimo = 2

Valor máximo = 26

mediana = 

Mediana = ^5to término = 11

Primer cuartil = valor medio de 2, 5, 7, 9

Eso es 

Así Primer Cuartil = 6

Tercer cuartil = valor medio de 18, 19, 25, 26

Eso es 

Así Tercer Cuartil = 22.