Demostrar tan2 θ – (1/cos2 θ) + 1 = 0

Es básicamente un estudio de las propiedades del triángulo y la función trigonométrica y su aplicación en diversos casos. Ayuda a encontrar los ángulos y los lados faltantes del triángulo con la ayuda de razones trigonométricas. Generalmente, se conocen los valores de algunos ángulos de los cuales obtenemos el valor de otros ángulos. Los ángulos de ángulo comúnmente conocidos son 0°, 30°, 45°, 60° y 90°.

La trigonometría es conocida por sus identidades. Las identidades trigonométricas se usan comúnmente para reescribir expresiones trigonométricas para simplificar una expresión, para obtener un tipo de expresión más útil o para desentrañar una ecuación. Los problemas en los que se utiliza un plano unidimensional se resuelven con la ayuda de la trigonometría plana. Las aplicaciones a problemas similares en más de un plano del espacio tridimensional se consideran en trigonometría.

razones trigonométricas

Las razones trigonométricas son las razones entre los lados de un triángulo rectángulo. Estas proporciones están dadas por las siguientes funciones trigonométricas del ángulo conocido, donde la perpendicular, la base y la hipotenusa se refieren a las longitudes de los lados en la siguiente figura,

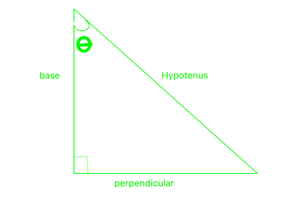
La hipotenusa es el lado opuesto al ángulo recto, es el lado más grande del triángulo. La base es el lado que contiene el ángulo. Perpendicular es el lado opuesto al ángulo dado.

Las seis funciones trigonométricas importantes (razones trigonométricas) se calculan utilizando las fórmulas a continuación y considerando la figura anterior. Es necesario conocer los lados del triángulo rectángulo porque define el conjunto de importantes funciones trigonométricas.

• El seno de θ se escribe como senθ y se define como la relación senθ = perpendicular/hipotenusa
• El coseno de θ se escribe como cosθ y se define como la relación cosθ = base/hipotenusa
• La tangente de θ se escribe como tanθ y se define como la relación tanθ = perpendicular/base = senθ/cosθ

Nota Los recíprocos de seno, coseno y tangentes también tienen nombres: son cosecante, secante y cotangente.               

• La cosecante de θ se escribe como cosecθ y se define como cosecθ = 1/sinθ
• La secante de θ se escribe como secθ y se define como secθ = 1/cosθ
• La cotangente de θ se escribe como cotθ y se define como cotθ = 1/tanθ

Tabla de razones trigonométricas

Anglos	0°	30°	45°	60°	90°
sen θ	0	1/2	1/√2	√3/2	1
cos θ	1	√3/2	1/√2	1/2	0
Bronceado θ	0	1/√3	1	√3	∞
Cosec θ	∞	2	√2	2/√3	1
segundo θ	1	2/√3	√2	2	∞
Cuna θ	∞	√3	1	1/√3	0

Hay tres identidades pitagóricas,

1. sen ² θ + cos ² θ = 1
2. bronceado ² θ + 1 = segundo ² θ
3. cuna ² θ + 1 = cosec ² θ

 Demostrar: tan ² θ – (1/cos ² θ) + 1 = 0

Solución:

Para probar – tan ² θ – (1/cos ² θ) + 1 = 0

Es sabido,

⇒ 1/cosθ = secθ

Entonces la ecuación se convierte en,

⇒ tan ² θ – seg ² θ + 1 = 0

De la identidad pitagórica, tan ² θ + 1 = sec ² θ

Entonces la ecuación se convierte en,

⇒ sec ² θ – sec ² θ que es claramente igual a 0

⇒ tan ² θ – (1/cos ² θ) + 1 = 0

Por lo tanto probado

Problemas de muestra

Pregunta 1: Encuentra el valor de sen ² x – cos ² x en términos de senx

Solución:

⇒ sen ² x + cos ² x = 1 [De la identidad pitagórica]

Asi que,

cos ² x = 1 – sen ² x 

Poniendo esto,

sen ² x – (1 – sen ² x) que es igual a

2sen ² x – 1

Pregunta 2: Encuentra el valor de 12tan ² x – 12sec ² x + 12

Solución:

⇒ 12tan ² x – 12seg ² x + 12 ⇢ 12(tan ² x – seg ² x) + 1

Se sabe, sec ² x – tan ² x = 1 [de la identidad pitagórica]

Entonces, la ecuación se convierte en 12(-1) + 12 = 0

12 tan ² x – 12 seg ² x + 12 = 0

Pregunta 3: Si tanx = 3 encuentra el valor de sec ² x + cosec ² x

Solución:

⇒ Se sabe, sec ² x = 1 + tan ² x [de la identidad pitagórica]

cosec ² x = 1 + cot ² x [de la identidad pitagórica]

Además, cotx = 1/tanx

La ecuación se convierte en 2 + tan ² x + cot ² x

Poniendo los valores,

2 + 9 + 1/9 = 100/9

seg ² x + cosec ² x, cuando tanx = 3 ⇒ 100/9