Podemos ver que hay 8 propiedades importantes de los determinantes que incluyen propiedad múltiple escalar, transposición de un determinante (propiedad de reflexión), intercambio de fila/columna (propiedad de cambio), determinante después de la operación de fila de agregar una proporción de una fila a otra, fila duplicada determinante (propiedad de repetición), si todos los elementos de cualquier columna o fila son cero, entonces el determinante es cero (propiedad de todo cero), si todos los elementos (propiedad de suma) de una fila o columnas en un determinante se expresan como una suma de dos o más números, entonces el determinante se puede descomponer como una suma de los correspondientes determinantes más pequeños, Determinante de la array triangular superior o triangular inferior (Propiedad de la Diagonal). Todas las propiedades determinantes se han cubierto a continuación de forma detallada junto con ejemplos resueltos.
Propiedad múltiple escalar
Si cualquier fila o columna de un determinante se multiplica por cualquier valor escalar, es decir, una constante distinta de cero, todo el determinante se multiplica por el mismo escalar, es decir, si cualquier fila o columna se multiplica por la constante k, el el valor determinante se multiplica por k. Las constantes pueden ser cualquier número real.
Ejemplo 1:
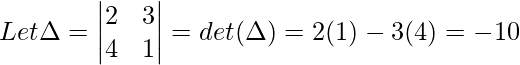
Ahora, al multiplicar por k = 1/2, primera fila,
det(Δ’) = 1(1) – 4(3/2) = -5
Por lo tanto det(Δ’) = 1/2 det(Δ)
⇒ det(Δ’) = k det(Δ)
Ejemplo 2:
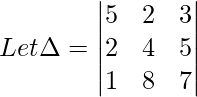
Ahora, al multiplicar por k = 3 , primera columna,
2
Por lo tanto det(Δ’) = 3/2 det(Δ)
⇒ det(Δ’) = k det(Δ)
Transposición de un determinante (Propiedad de reflexión)
La transposición se refiere a las operaciones de intercambiar filas y columnas del determinante. Las filas se convierten en columnas y las columnas en filas en orden. Se denota por |A T |, para cualquier determinante |A|.
La propiedad dice que el determinante permanece sin cambios en su transpuesta, es decir, |A T | = |A| .
Ejemplo 1:
⇒ det(A) = det(A T )
Ejemplo 2:
Intercambio de fila/columna (propiedad de cambio)
Si intercambiamos dos filas/columnas cualesquiera del determinante, la magnitud (es decir, el signo) cambia, pero el valor del determinante sigue siendo el mismo.
Ahora valor determinante = (-1) número de intercambios
Ejemplo 1:
Si intercambiamos C 1 y C 3 , denotados por C 1 ↔ C 3
det (Δ) = -det(Δ’)
Si intercambiamos de nuevo R 1 y R 2 , denotados por R 1 ↔ R 2
det(Δ”) = -det(Δ’)
= det (Δ)
Ejemplo 2:
Realizando una operación de fila, obtenemos,
Si intercambiamos R 1 y R 2, denotados por R 1 ↔ R 2
det(Δ) = – det(Δ’)
Si intercambiamos de nuevo R 2 y R 3 , denotados por R 2 ↔ R 3
det(Δ”) = – det(Δ’)
= det(Δ)
Determinante después de la operación de fila de sumar una proporción de una fila a otra
Si se suma un múltiplo de una fila a otra fila de determinante, sus valores permanecen sin cambios.
Ejemplo 1:
det (Δ) = 1 + (-26) = -25
R 1 ⇠ R 1 + 2R 2
det (Δ’) = -6 + (-7)(-1) + (-26)
= -6 + 7 – 26
= -25
det (Δ) = det (Δ’)
Ejemplo 2:
det(Δ) = [8{(5 × 7) – (9 × 3)} – 6{(1 × 7) – (0 × 3)} + 8{(1 × 9) – (5 × 0)} ]
det(Δ) = 94R 3 ⇢ R 3 + 2R 2
det(Δ’) = [8{(5 × 7) – (9 × 5)} – 6{(1 × 7) – (0 × 5)} + 24{(1 × 9) – (5 × 0) }]
det(Δ’) = 94det (Δ) = det (Δ’)
Determinante de fila duplicada (Propiedad de repetición)
Si cualquier par de filas o columnas de un determinante son exactamente idénticas o proporcionales en la misma cantidad, entonces el determinante es cero
Ejemplo 1:
det(Δ) = [1{(2 × 0) – (-8 × 3) – 1{(2 × 0) – (-8 × 3)} + 4{(2 × 3) – (2 × 3) }]
det(Δ) = 0 (dado que R 1 y R 2 son idénticos)
Ejemplo 2:
det(Δ) = [8{(6 × 7) – (6 × 7)} – 5{(1 × 7) – (6 × 0)} + 5{(1 × 7) – (6 × 0)} ]
det(Δ) = 0 (dado que R 2 y R 3 son idénticos)
Todo Cero Propiedad
Si todos los elementos de cualquier columna o fila son cero, entonces el determinante es cero
Ejemplo 1:
det(Δ) = 0 (ya que C 1 ⇢0)
Ejemplo 2:
det(Δ) = 0 (ya que R 2 ⇢0)
Propiedad de suma
Si todos los elementos de una fila o columna en un determinante se expresan como una suma de dos o más números, entonces el determinante se puede descomponer como una suma de los correspondientes determinantes más pequeños .
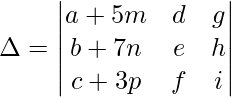

Propiedad diagonal
Si todos los elementos del determinante por encima o por debajo de la diagonal son cero, entonces el determinante es un producto de los elementos de la diagonal.
Ejemplo 1:
Ejemplo 2:
det(Δ) = 2×1×8×9 = 144

























