prueba de levene – Barcelona Geeks

La prueba de Levene se utiliza para evaluar la igualdad de varianza entre dos muestras diferentes. Para cada caso, calcula la diferencia absoluta entre el valor de ese caso y la media de su celda y realiza un análisis de varianza (ANOVA) de una vía sobre esas diferencias.

suposiciones

Las muestras de las poblaciones consideradas son independientes.
Las poblaciones bajo consideración tienen una distribución aproximadamente normal.

Cómo realizar la prueba de Levene

La hipótesis nula de la prueba de Levene es que la varianza entre los grupos es igual.

$H_0 : \sigma_{1}^{2} = \sigma_{2}^{2} = \sigma_{3}^{2} ... = \sigma_{n}^{2}$

La hipótesis alternativa es que la varianza entre diferentes grupos no es igual (para al menos un par la varianza no es igual a los demás).

$H_A : \sigma_{1}^{2} \neq \sigma_{2}^{2} \neq \sigma_{3}^{2} ... \neq \sigma_{n}^{2}$

Las estadísticas de prueba para la prueba de Levene son:

$W = \frac{\left ( N - k \right )\sum_{i=1}^{K}N_{i} \left ( Z_{i} - Z.. \right )^2}{ \left ( K-1 \right )\sum_{i=1}^{K} \sum_{j=1}^{N_i}\left ( Z_{ij}- Z_i \right )^2}$

dónde,
- k:

$Z_{ij} = \begin{Bmatrix} \left | Y_{ij} - \bar{Y_i} \right |, \bar{Y_i} \, is \, the \, mean \, of \, the \, i^{th} \, group \\ \left | Y_{ij} - \tilde{Y_i} \right |, \tilde{Y_i} \, is \, the \, median \, of \, the \, i^{th} \, group \end{Bmatrix}$

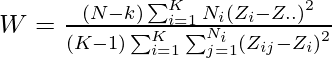
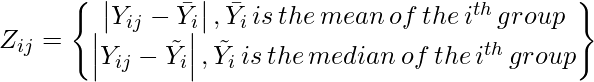
dónde,
- Y _ij : el valor del j ^-ésimo caso y del i ^-ésimo grupo.

$Z_i. = \frac{1}{N_i}\sum_{j=1}^{N_i}Z_{ij} \, where \, Z_{ij} \,is \, the\, mean \, of \, for \, group \, i$ [Tex]Z_{..} = \frac{1}{N_i}\sum_{i=1}^{K}\sum_{j=1}^{N_i}Z_{ij} \, where \, Z_{ij} \,is \, the\, mean \, of \, all. [/Tex]

Hay tres tipos de estadísticas de Levene disponibles
- Si una distribución tiene una distribución de cola más larga como la distribución de Cauchy, entonces usamos la media recortada.
- Para una distribución sesgada, si la distribución no es clara, usaremos la mediana para las estadísticas de prueba.
- Para la distribución simétrica y la distribución de cola moderada, usamos el valor medio para la distribución.
Decidir el nivel de significación (alfa). Generalmente, lo tomamos como 0.05.
Encuentre el valor crítico en la tabla de distribución F para el nivel de significación dado, los parámetros (Nk) y (k-1).
- Si W > F _{∝, k-1, Nk,} entonces rechazamos la hipótesis nula.
- caso contrario, no rechazamos la hipótesis nula.

Ejemplo:

Supongamos que hay 2 grupos de estudiantes cuyos puntajes en una prueba de matemáticas están a continuación:

Grupo 1	Grupo 2
14	34
34	36
dieciséis	44
43	18
45	42
36	39
42	dieciséis
43	35
dieciséis	15
27	33

Aquí, nuestra hipótesis nula se define como:

$H_0 : \sigma_{1}^{2} = \sigma_{2}^{2}$

y la hipótesis alternativa es

$H_A : \sigma_{1}^{2} \neq \sigma_{2}^{2}$

Y nuestro nivel de significación es:

$\alpha = 0.05$

Ahora, calcule las estadísticas de prueba usando la fórmula anterior

	Grupo 1	Grupo 2	G1 (Y) : ( _Xi – Media)	G2 (Z) : ( _Xi – Media)	( Yi – _mediaVar ) ²	( Zi – _mediaVar ) ²
	14	34	2.8	17.6	49	60.84
	34	36	4.8	2.4	25	54.76
	dieciséis	44	12.8	15.6	9	33.64
	43	18	13.2	11.4	11.56	2.56
	45	42	10.8	13.4	1	12.96
	36	39	7.8	4.4	4	29.16
	42	dieciséis	15.2	10.4	29.16	0.36
	43	35	3.8	11.4	36	2.56
	dieciséis	15	16.2	15.6	40.96	33.64
	27	33	1.8	4.6	64	27.04
Promedio	31.6	31.2	8.92	10.68

donde, mediaVar es,

$meanVar = \frac{10 * 8.92 + 10 * 10.68}{20}$

y k-1 = Número de grupos -1 =1
Nk = 20-2 =18.
Resolviendo las estadísticas de prueba usando los siguientes parámetros

$W = \frac{18* 15.488}{1* 511.712}$ [Tex]W = 0.54481[/Tex]

Dado que W < F _0.05,1,19 , no rechazamos la hipótesis nula.

Implementación:

Python3

from scipy.stats import levene
# define groups
group_1 = [14, 34, 16, 43, 45, 36, 42, 43, 16, 27]
group_2 = [34, 36, 44, 18, 42, 39, 16, 35, 15, 33]
 
# define alpha
alpha =0.05
# now we pass the groups and center value from the following
# ('trimmed mean', 'mean', 'median')
w_stats, p_value =levene(group_1,group_2, center ='mean')
 
if p_value > alpha :
  print("We do not reject the null hypothesis")
else:
  print("Reject the Null Hypothesis")

We do not reject the null hypothesis

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

suposiciones

Cómo realizar la prueba de Levene

Ejemplo:

Implementación:

Python3

Deja una respuesta Cancelar la respuesta