Pregunta 1(i). Resuelve gráficamente los siguientes sistemas de inecuaciones lineales:
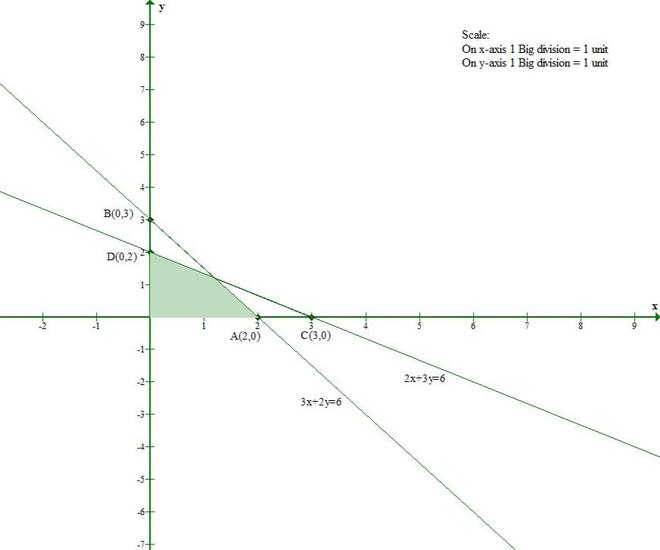
2x + 3y ≤ 6
3x + 2y ≤ 6
x ≥ 0, y ≥ 0
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
2x + 3y = 6 -(1)
3x + 2y = 6 -(2)
x = 0 -(3)
y = 0 -(4)
Consideremos la ecuación (1)
La línea 2x + 3y = 6 se encuentra con el eje x en (3, 0) y el eje y en (0, 2).
Y Origen(0, 0) satisface la inecuación 2x + 3y ≤ 6.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 2x + 3y ≤ 6.
Consideremos la ecuación (2)
La línea 3x + 2y = 6 se encuentra con el eje x en (2, 0) y el eje y en (0, 3).
Y Origen(0, 0) satisface la inecuación 3x + 2y ≤ 6.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 3x + 2y ≤ 6.
x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Así, la región sombreada representa la solución de las inecuaciones dadas.
Pregunta 1(ii). Resuelve gráficamente los siguientes sistemas de inecuaciones lineales:
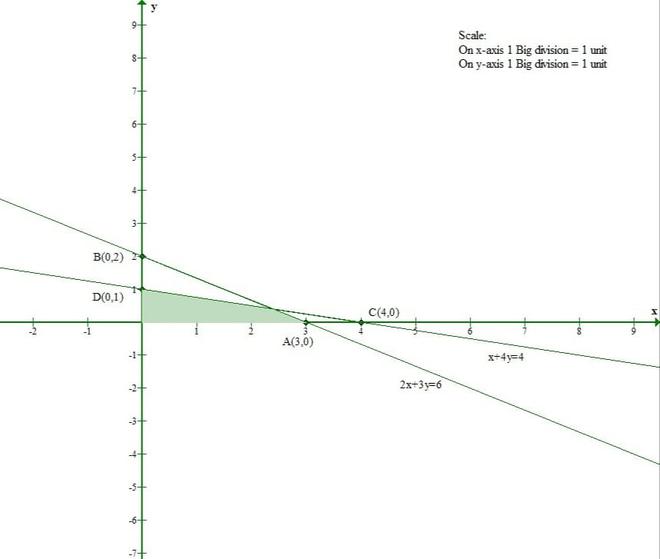
2x + 3y ≤ 6
x + 4y ≤ 4
x ≥ 0, y ≥ 0
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
2x + 3y = 6 -(1)
x + 4y = 4 -(2)
x = 0 -(3)
y = 0 -(4)
Consideremos la ecuación (1)
La línea 2x + 3y = 6 se encuentra con el eje x en (3, 0) y el eje y en (0, 2).
Y Origen(0, 0) satisface la inecuación 2x + 3y ≤ 6.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 2x + 3y ≤ 6.
Consideremos la ecuación (2)
La línea x + 4y = 4 se encuentra con el eje x en (4, 0) y el eje y en (0, 1).
Y Origen(0, 0) satisface la inecuación x + 4y ≤ 4.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + 4y ≤ 4.
x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Por lo tanto, la región sombreada representa el conjunto solución de inecuaciones dadas.
Pregunta 1(iii). Resuelve gráficamente los siguientes sistemas de ecuaciones lineales:
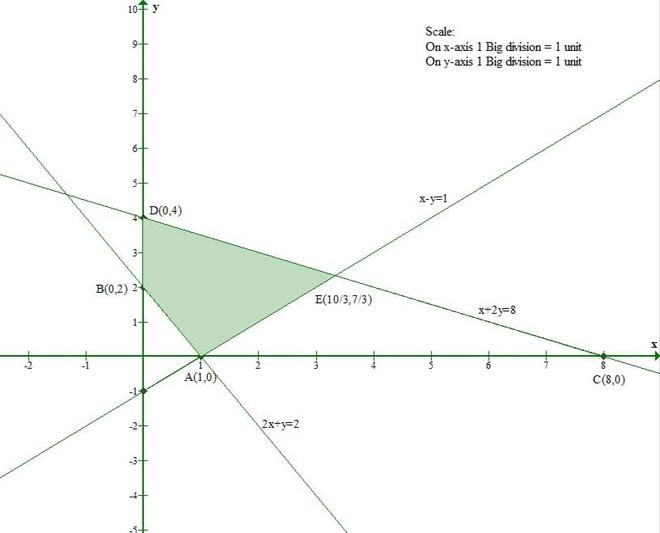
x – y ≤ 1
x + 2y ≤ 8
2x + y ≥ 2
x ≥ 0, y ≥ 0
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
x – y = 1 – (1)
x + 2y = 8 -(2)
2x + y = 2 -(3)
x = 0, y = 0 -(4)
Consideremos la ecuación (1)
La línea x – y = 1 se encuentra con el eje x en (1, 0) y el eje y en (0, -1).
Y Origen(0, 0) satisface la inecuación x – y ≤ 1
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x – y ≤ 1.
Consideremos la ecuación (2)
La línea x + 2y = 8 se encuentra con el eje x en (8, 0) y el eje y en (0, 4).
Y Origen(0, 0) satisface la inecuación x + 2y ≤ 8.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + 2y ≤ 8.
Consideremos la ecuación (3)
La línea 2x + y = 2 se encuentra con el eje x en (1, 0) y el eje y en (0, 2).
Y Origen(0, 0) no satisface la inecuación 2x + y ≥ 2.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 2x + y ≥ 2.
x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Así, la región sombreada representa el conjunto solución de inecuaciones dadas.
Pregunta 1(iv). Resuelve gráficamente los siguientes sistemas de ecuaciones lineales:
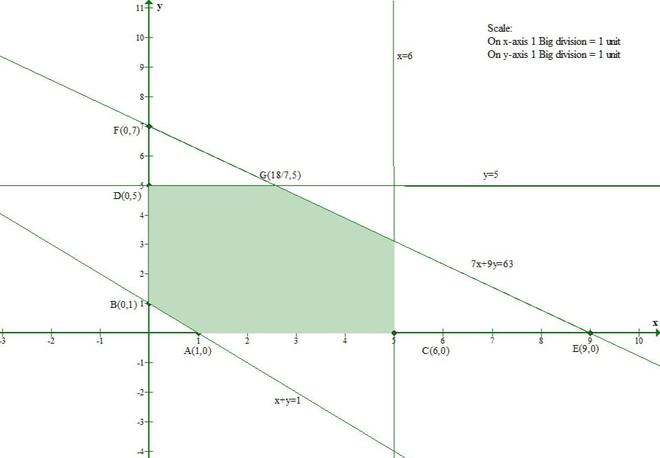
x + y ≥ 1
7x + 9y ≤ 63
X ≤ 6
y ≤ 5
x ≥ 0, y ≥ 0
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
x + y = 1 -(1)
7x + 9y = 63 -(2)
x = 6 -(3)
y = 5 -(4)
x = 0, y = 0
Consideremos la ecuación (1)
La línea x + y= 1 se encuentra con el eje x en (1, 0) y el eje y en (0, 1).
Y Origin(0, 0) no satisface la inecuación x + y ≥ 1.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + y ≥ 1.
Consideremosq(2)
La línea 7x + 9y = 63 se encuentra con el eje x en (9, 0) y el eje y en (0, 7).
Y Origen(0, 0) satisface la inecuación 7x + 9y ≤ 63.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 7x + 9y ≤ 63.
Consideremos la ecuación (3)
La línea x = 6 es paralela al eje y y está a una distancia de 6 unidades de él.
Y Origen(0, 0) satisface la inecuación x ≤ 6.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x ≤ 6.
Consideremos la ecuación (4)
La línea y = 5 es paralela al eje x y está a una distancia de 5 unidades de él.
Y Origin(0, 0) satisface la inecuación y ≤ 5.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación y ≤ 5.
x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Por lo tanto, la región sombreada representa los conjuntos de soluciones de las inecuaciones dadas.
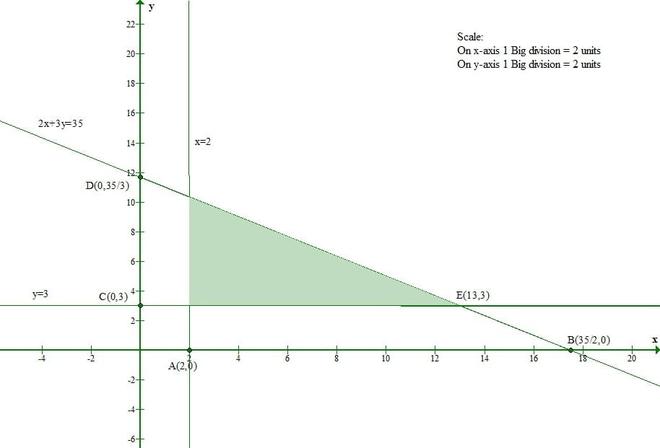
Pregunta 1(v). Resuelve gráficamente los siguientes sistemas de ecuaciones lineales:
2x + 3y ≤ 35
y ≥ 3
X ≥ 2
x ≥ 0, y ≥ 0
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
2x + 3y = 35 -(1)
y = 3 -(2)
x = 2 -(3)
x = 0, y = 0
Consideremos la ecuación (1)
La línea 2x + 3y = 35 se encuentra con el eje x en (35/2, 0) y el eje y en (0, 35/3).
Y Origen(0, 0) satisface la inecuación 2x + 3y ≤ 35.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 2x + 3y ≤ 35.
Consideremos la ecuación (2)
La línea y = 3 es paralela al eje x y está a una distancia de 3 unidades de él.
Y Origen(0, 0) no satisface la inecuación y ≥ 3.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación y ≥ 3.
Consideremos la ecuación (3)
La línea x = 2 es paralela al eje y y está a una distancia de 2 unidades de él.
Y Origen(0, 0) no satisface la inecuación x ≥ 2.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x ≥ 2.
x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Por lo tanto, la región sombreada representa los conjuntos de soluciones de las inecuaciones dadas.
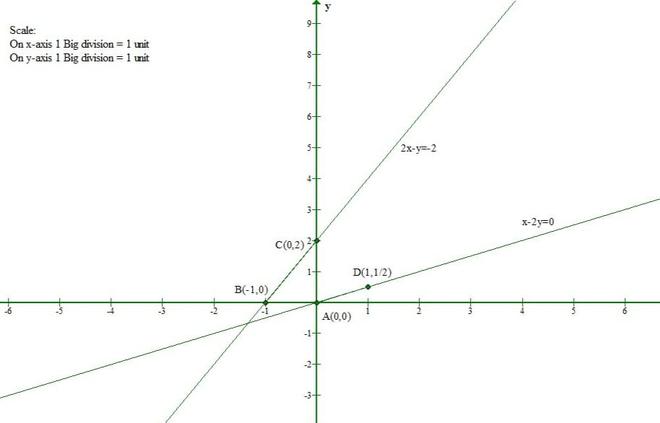
Pregunta 2(i). Demuestre que el conjunto solución de las siguientes ecuaciones lineales es un conjunto vacío:
x – 2y ≥ 0
2x – y ≤ -2
X ≥ 0
y ≥ 0
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
x-2y = 0- ( 1)
2x – y = -2 -(2)
x = 0 -(3)
y = 0 -(4)
Consideremos la ecuación (1)
La línea x – 2y = 0 se encuentra con el eje x en (0, 0) y el eje y en (0, 0).
Si x = 1 entonces y = 1/2
Y Origen(0, 0) satisface la inecuación x – 2y ≥ 0.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x – 2y ≥ 0.
Consideremos la ecuación (2)
La línea 2x – y = -2 se encuentra con el eje x en (-1, 0) y el eje y en (0, 2).
Y Origin(0, 0) no satisface la inecuación 2x – y ≤ -2.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 2x – y ≤ -2.
Claramente, x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Del gráfico dado concluimos que no hay una región común en todas las líneas.
Entonces, el conjunto solución de las inecuaciones dadas está vacío.
Por lo tanto probado
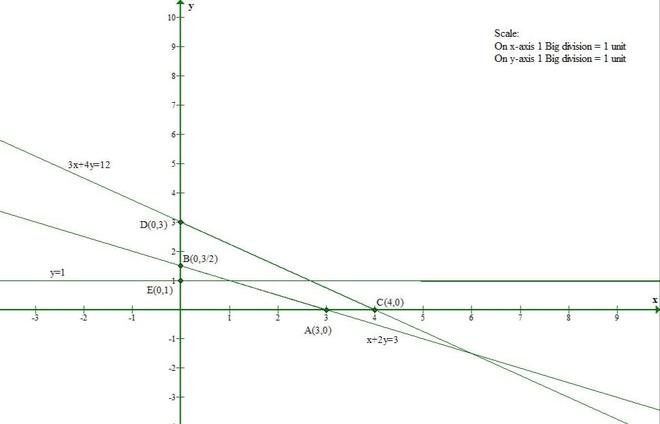
Pregunta 2(ii). Demuestre que el conjunto solución de las siguientes ecuaciones lineales es un conjunto vacío:
x + 2y ≤ 3
3x + 4y ≥ 12
y ≥ 1
X ≥ 0
y ≥ 0
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
x + 2y = 3 -(1)
3x + 4y = 12 -(2)
y = 1 -(3)
x = 0 -(4)
y = 0 -(5)
Consideremos la ecuación (1)
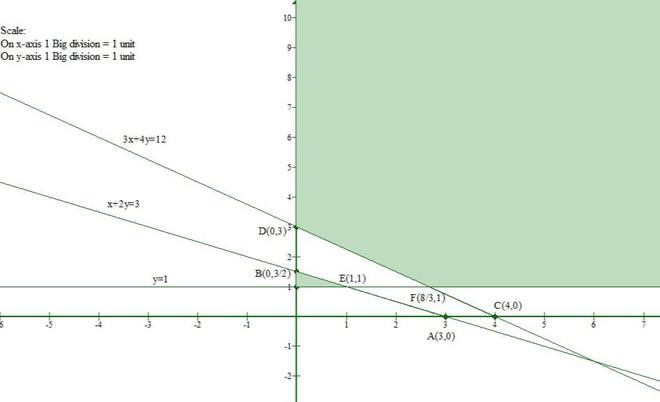
La línea x + 2y = 3 se encuentra con el eje x en (3, 0) y el eje y en (0, 3/2).
Y Origen(0, 0) satisface la inecuación x + 2y ≤ 3.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + 2y ≤ 3.
Consideremos la ecuación (2)
La línea 3x + 4y = 12 se encuentra con el eje x en (4, 0) y el eje y en (0, 3).
Y Origen(0, 0) no satisface la inecuación 3x + 4y ≥ 12.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 3x + 4y ≥ 12.
Consideremosq(3)
La línea y = 1 es paralela al eje x y está a una distancia de 1 unidad de él.
Y Origen(0, 0) no satisface la inecuación y ≥ 1.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación y ≥ 1.
x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Del gráfico dado concluimos que no hay una región común en todas las líneas.
Entonces, el conjunto solución de las inecuaciones dadas está vacío.
Por lo tanto probado
Pregunta 3. Encuentre las inecuaciones lineales para las cuales la región sombreada en la siguiente figura es el conjunto de soluciones. Dibuja el diagrama para el conjunto solución de inecuaciones lineales.
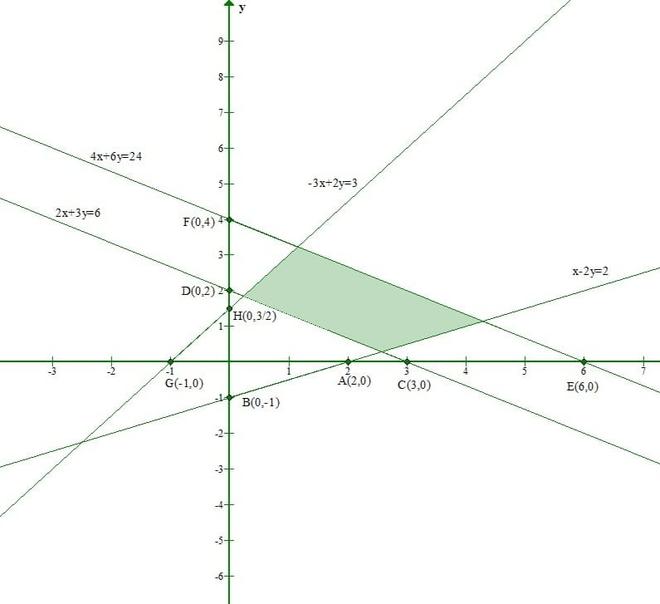
Solución:
Consideremos la recta 2x + 3y = 6
La región sombreada y el origen (0, 0) están en el lado opuesto de esta línea.
Y Origen(0, 0) no satisface la inecuación 2x + 3y ≥ 6
Consideremos la recta 4x + 6y = 24
La región sombreada y el origen (0, 0) están del mismo lado de esta línea.
Y Origen(0, 0) satisface la inecuación 4x + 6y ≤ 24
Consideremos la recta x – 2y = 2
La región sombreada y el origen (0, 0) están del mismo lado de esta línea.
Y Origen(0, 0) satisface la inecuación x – 2y ≤ 2
Consideremos la recta -3x + 2y = 3
La región sombreada y el origen (0, 0) están del mismo lado de esta línea.
Y Origen(0, 0) satisface la inecuación -3x + 2y ≤ 3
Ya que la parte sombreada está en el primer cuadrante.
También tenemos que tomar x ≥ 0 y y ≥ 0.
Así, las ecuaciones lineales que componen el conjunto solución dado son:
2x + 3y ≥ 6, 4x + 6y ≤ 24, x – 2y ≤ 2, -3x + 2y ≤ 3, x ≥ 0 y y≥. 0.
Pregunta 4. Encuentra las inecuaciones lineales para las cuales el conjunto solución es la región sombreada que se muestra a continuación.
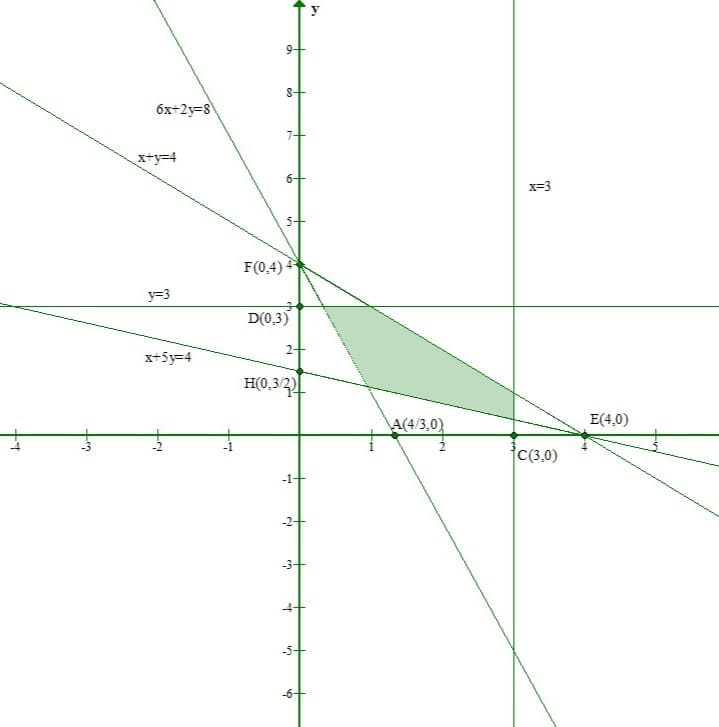
Solución:
Consideremos la línea x + y = 4
La región sombreada y el origen (0, 0) están del mismo lado de esta línea.
Y Origen(0, 0) no satisface la inecuación x + y ≤ 4
Consideremos la línea y = 3
La región sombreada y el origen (0, 0) están del mismo lado de esta línea.
Y Origin(0, 0) satisface la inecuación y ≤ 3.
Consideremos la línea x = 3
La región sombreada y el origen (0, 0) están del mismo lado de esta línea.
Y Origen(0, 0) satisface la inecuación x ≤ 3.
Consideremos la línea x + 5y = 4
La región sombreada y el origen (0, 0) están en el lado opuesto de esta línea.
Y Origen(0, 0) no satisface la inecuación x + 5y ≥ 4.
Consideremos la línea 6x + 2y = 8
La región sombreada y el origen (0, 0) están en el lado opuesto de esta línea.
Y Origen(0, 0) no satisface la inecuación 6x + 2y ≥ 8.
Ya que la parte sombreada está en el primer cuadrante.
También tenemos que tomar x ≥ 0 y y ≥ 0.
Así, las ecuaciones lineales que componen el conjunto solución dado son:
x + y ≤ 4, x ≤ 3, y ≤ 3 x + 5y ≥ 4, 6x + 2y ≥ 8, x ≥ 0 y y ≥ 0.
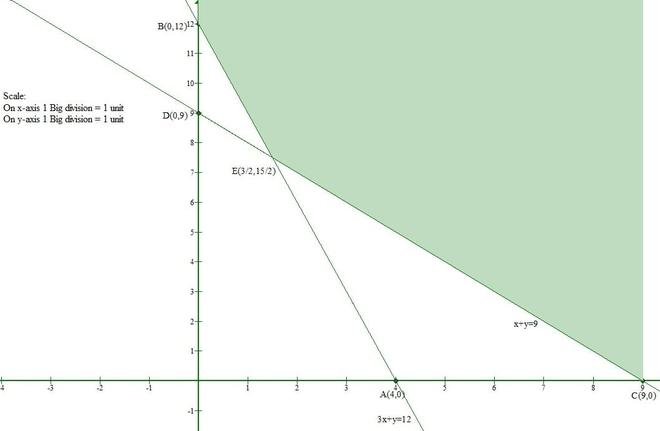
Pregunta 5. Muestre que el conjunto solución de las siguientes inecuaciones lineales es un conjunto ilimitado:
x + y ≥ 9
3x + y ≥ 12
x ≥ 0 y y ≥ 0.
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
x + y = 9 -(1)
3x + y = 12 -(2)
x = 0 y y = 0 -(3)
Consideremos la ecuación (1)
La línea x + y = 9 se encuentra con el eje x en (9, 0) y el eje y en (0, 9).
Y Origin(0, 0) no satisface la inecuación x + y ≥ 9.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + y ≥ 9.
Consideremos la ecuación (2)
La línea 3x + y = 12 se encuentra con el eje x en (4, 0) y el eje y en (0, 12).
Y Origin(0, 0) no satisface la inecuación 3x + y ≥ 12.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 3x + y ≥ 12.
Claramente, x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Por lo tanto, el conjunto solución se encuentra en el primer cuadrante.
Del gráfico dado concluimos que la región sombreada no está acotada.
Por lo tanto, el conjunto solución del conjunto dado de desigualdades es un conjunto ilimitado.
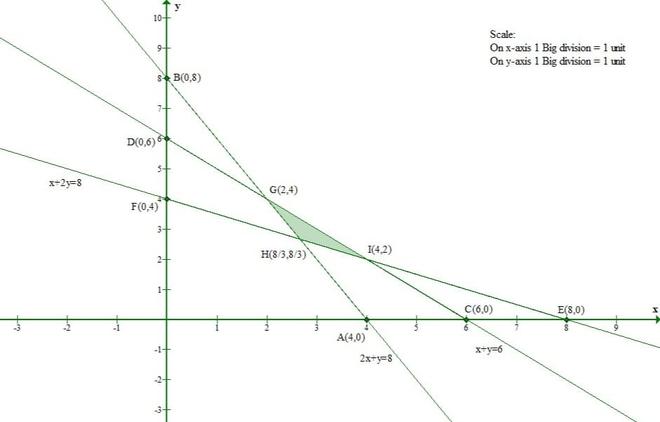
Pregunta 6(i). Resuelve gráficamente los siguientes sistemas de inecuaciones:
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
2x + y = 8 -(1)
x + 2y = 8 -(2)
x + y = 6 -(3)
Consideremos la ecuación (1)
La línea 2x + y = 8 se encuentra con el eje x en (4, 0) y el eje y en (0, 8).
Y Origin(0, 0) no satisface la inecuación 2x + y ≥ 8.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 2x + y ≥ 8.
Consideremos la ecuación (2)
La línea x + 2y ≥ 8 se encuentra con el eje x en (8, 0) y el eje y en (0, 4).
Y Origen(0, 0) no satisface la inecuación x + 2y ≥ 8.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + 2y ≥ 8.
Consideremos la ecuación (3)
La línea x + y = 6 se encuentra con el eje x en (6, 0) y el eje y en (0, 6).
Y Origin(0, 0) satisface la inecuación x + y ≤ 6.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + y ≤ 6.
Por lo tanto, la solución establecida para las inequidades es la intersección de las tres soluciones anteriores.
Por lo tanto, la región sombreada representa el conjunto solución del conjunto dado de inequidades.
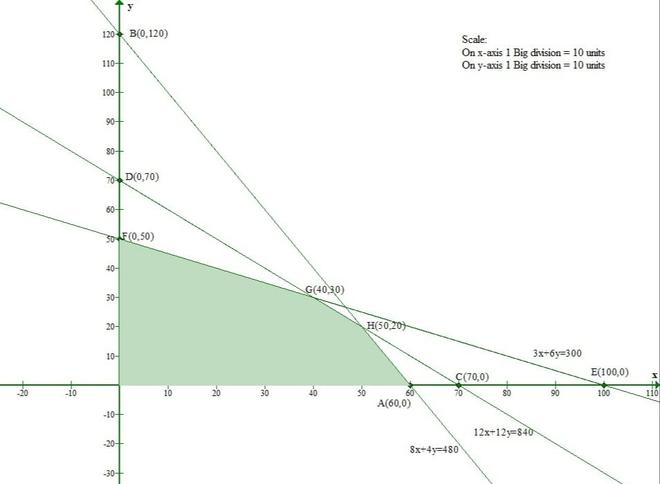
Pregunta 6(ii). Resuelve gráficamente los siguientes sistemas de inecuaciones:
12x + 12y ≤ 840, 3x + 6y ≤ 300, 8x + 4y ≤ 480, x ≥ 0 y y ≥ 0.
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
12x + 12y = 840 -(1)
3x + 6y = 300 -(2)
8x + 4y = 480 -(3)
x = 0 y y = 0 -(4)
Consideremos la ecuación (1)
La línea 12x + 12y = 840 se encuentra con el eje x en (70, 0) y el eje y en (0, 70).
Y Origen(0, 0) satisface la inecuación 12x + 12y ≤ 840.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 12x + 12y ≤ 840.
Consideremos la ecuación (2)
La línea 3x + 6y = 300 se encuentra con el eje x en (100, 0) y el eje y en (0, 50).
Y Origen(0, 0) satisface la inecuación 3x + 6y ≤ 300.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 3x + 6y ≤ 300.
Consideremosq(3)
La línea 8x + 4y = 480 se encuentra con el eje x en (60, 0) y el eje y en (0, 120).
Y Origen(0, 0) satisface la inecuación 8x + 4y ≤ 480.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 8x + 4y ≤ 480.
Claramente, x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Por lo tanto, la solución establecida para las inequidades es la intersección de las tres soluciones anteriores.
Por lo tanto, la región sombreada representa el conjunto solución del conjunto dado de desigualdades.
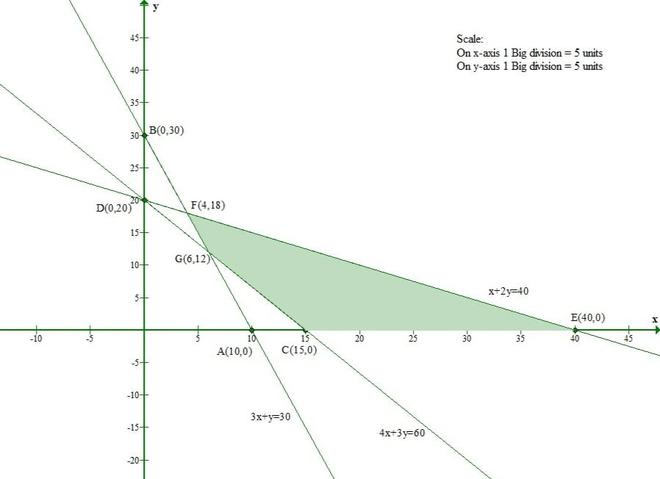
Pregunta 6(iii). Resuelve gráficamente los siguientes sistemas de inecuaciones:
x + 2y ≤ 40, 3x + y ≥ 30, 4x + 3y ≥ 60, x ≥ 0 y y ≥ 0.
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
x + 2y = 40 -(1)
3x + y = 30 -(2)
4x + 3y = 60 -(3)
x = 0 y y = 0 -(4)
Consideremos la ecuación (1)
La línea x + 2y = 40 se encuentra con el eje x en (40, 0) y el eje y en (0, 20).
Y Origen(0, 0) satisface la inecuación x + 2y ≤ 40.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + 2y ≤ 40.
Consideremos la ecuación (2)
La línea 3x + y = 30 se encuentra con el eje x en (10, 0) y el eje y en (0, 30).
Y Origen(0, 0) no satisface la inecuación 3x + y ≥ 30.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 3x + y ≥ 30.
Consideremos la ecuación (3)
La línea 4x + 3y = 60 se encuentra con el eje x en (15, 0) y el eje y en (0, 20).
Y Origen(0, 0) no satisface la inecuación 4x + 3y ≥ 60.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 4x + 3y ≥ 60.
Claramente, x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Por lo tanto, la solución establecida para las inequidades es la intersección de las tres soluciones anteriores.
Por lo tanto, la región sombreada representa el conjunto solución del conjunto dado de desigualdades.
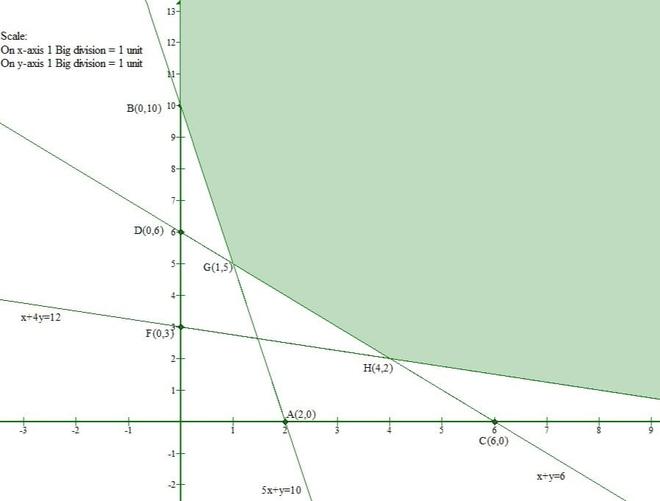
Pregunta 6(iv) Resuelva gráficamente los siguientes sistemas de inecuaciones:
5x + y ≥ 10, 2x + 2y ≥ 12, x + 4y ≥ 12, x ≥ 0 y y ≥ 0.
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
5x + y = 10 -(1)
2x + 2y = 12 -(2)
x + 4y = 12 -(3)
x = 0 y y = 0 -(4)
Consideremos la ecuación (1)
La línea 5x + y = 10 se encuentra con el eje x en (2, 0) y el eje y en (0, 10).
Y Origen(0, 0) no satisface la inecuación 5x + y ≥ 10.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 5x + y ≥ 10.
Consideremosq(2)
La línea 2x + 2y = 12 se encuentra con el eje x en (6, 0) y el eje y en (0, 6).
Y Origen(0, 0) no satisface la inecuación 2x + 2y ≥ 12.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación 2x + 2y ≥ 12.
Consideremos la ecuación (3)
La línea x + 4y = 12 se encuentra con el eje x en (12, 0) y el eje y en (0, 3).
Y Origen(0, 0) no satisface la inecuación x + 4y ≥ 12.
Entonces, la sección que contiene el origen representará el conjunto solución de la inecuación x + 4y ≥ 12.
Claramente, x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Por lo tanto, la solución establecida para las inequidades es la intersección de las tres soluciones anteriores.
Por lo tanto, la región sombreada representa el conjunto solución del conjunto dado de desigualdades.
Pregunta 7. Demuestre que el siguiente sistema de ecuaciones lineales no tiene soluciones
x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solución:
Convirtamos las inecuaciones dadas en ecuaciones.
x + 2y = 3 -(1)
3x + 4y = 12 -(2)
x = 0 y y = 1 -(3)
Los puntos que satisfacen la ecuación (1) son
X 3 0 5 y 0 1.5 -1 Los puntos que satisfacen la ecuación (2) son
X 0 4 8 y 3 0 -3 Ahora, dibujemos la gráfica que representa las inecuaciones dadas
Entonces, del gráfico anterior podemos observar que no hay una región común.
Por lo tanto, podemos decir que el conjunto solución de estas desigualdades no tiene solución.
Pregunta 8. Muestre que el conjunto solución del siguiente sistema de inecuaciones lineales es una región ilimitada:
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0
Solución:
Dado que
2x + y ≥ 8 -(1)
x + 2y ≥ 10 -(2)
x ≥ 0 -(3)
y ≥ 0 -(4)
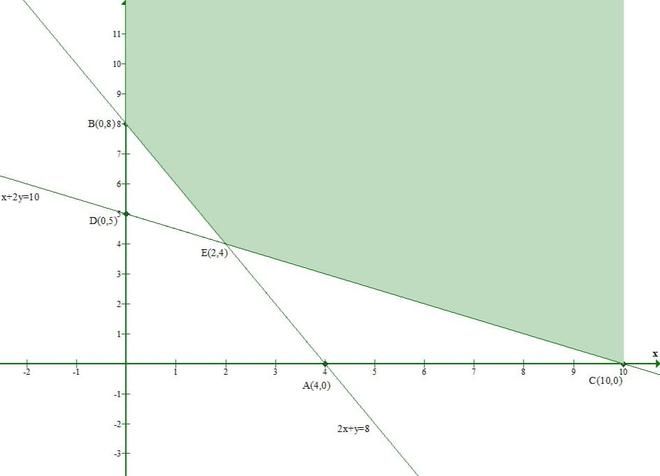
Los puntos que satisfacen la recta 2x + y = 8 son
X 0 4 2 y 8 0 4 Los puntos que satisfacen x + 2y = 10 son
X 0 10 2 y 5 0 4 Claramente, x ≥ 0 y y ≥ 0 representan el primer cuadrante.
Dibujemos la gráfica que representa las inecuaciones dadas
Dado que la región sombreada común es el conjunto solución de un conjunto dado de inequidades.
Por lo tanto, demostramos que el conjunto solución de inecuaciones lineales dadas es una región ilimitada.
Publicación traducida automáticamente
Artículo escrito por prasanthinidamarthy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA