Pregunta 1. Haz un bosquejo de las siguientes gráficas:
(i) y = 2 sen 2x
Solución:
Para obtener este gráfico y = 2 sen 2x,
Primero dibujamos la gráfica de y = sen x y luego dividimos las coordenadas x de los puntos donde cruza el eje x por 2.
Los valores máximo y mínimo de y son 2 y -2 respectivamente.
(ii) y = 3 sen x
Solución:
Para obtener este gráfico y = 3 sen x,
Primero dibujamos la gráfica de y = sen x.
Los valores máximo y mínimo de y son 3 y -3 respectivamente.
(iii) 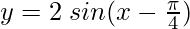
Solución:
Para obtener este gráfico y-0 =
,
Al desplazar el origen en (/4, 0), obtenemos
X =
y Y = y – 0
Al sustituir estos valores, obtenemos
Y = 2 sen X
Primero dibujamos la gráfica de Y = 2 sen X y la desplazamos /4 hacia la derecha.
(iv) y = 2 sen (2x – 1)
Solución:
Para obtener este gráfico y – 0 = 2 sen
,
Al desplazar el origen en (1/2, 0), obtenemos
X =
y Y = y – 0
Al sustituir estos valores, obtenemos
Y = 2 sen 2X
Primero dibujamos la gráfica de Y = 2 sen 2X y la desplazamos 1/2 a la derecha.
(v) y = 3 sen (3x + 1)
Solución:
Para obtener este gráfico y – 0 = 3 sen 3
,
Al desplazar el origen en (-1/3, 0), obtenemos
X =
y Y = y – 0
Al sustituir estos valores, obtenemos
Y = 3 sen 3X
Primero dibujamos la gráfica de Y = 3 sen 3X y la desplazamos 1/3 hacia la izquierda.
(vi) 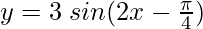
Para obtener esta gráfica y-0 =
Al desplazar el origen en (/8, 0), obtenemos
X =
e Y = y-0
Al sustituir estos valores, obtenemos
Y = 3 sen 2X
Primero dibujamos la gráfica de Y = 3 sen 2X y la desplazamos /8 hacia la derecha.
Pregunta 2: Dibuja la gráfica de los siguientes pares de funciones en los mismos ejes:
(i) y = sen x, 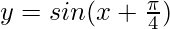
Gráfico 1:
y = sen x
Gráfico 2:
Para obtener esta gráfica y-0 =
Al desplazar el origen en (-/4, 0), obtenemos
X =
y Y = y – 0
Al sustituir estos valores, obtenemos
Y = sen X
Primero dibujamos la gráfica de Y = sen X y la desplazamos /4 hacia la izquierda.
La gráfica y = sen x y
están en diferentes ejes es la siguiente:
(ii) y = sen x, y = sen 3x
Gráfico 1:
y = sen x
Gráfico 2:
Para obtener este gráfico y = sen 3x,
Primero dibujamos la gráfica de y = sen x y luego dividimos las coordenadas x de los puntos donde cruza el eje x por 3.
La gráfica y = sen x y y = sen 3x están en diferentes ejes son las siguientes:













