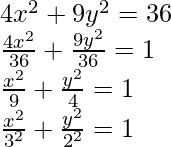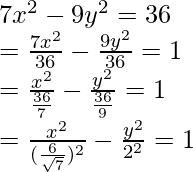Identificar secciones cónicas a partir de su ecuación

Las secciones cónicas son curvas generadas cuando un plano se cruza con un cono circular recto en diferentes ángulos. Sección cónica tiene la definición en su nombre, es una sección formada por el corte de un Cono. Cada tipo de intersección da diferentes tipos de curvas. Dependiendo del ángulo de intersección del plano, la forma de la curva varía y forma diferentes curvas como parábola, hipérbola, elipse, etc.  

Podemos obtener las siguientes curvas a partir de las intersecciones: 

1. Circulo
2. Parábola
3. Hipérbola
4. Elipse

Hay ciertas características que son comunes a las ecuaciones de cada curva. Estudiemos cada uno de ellos y veamos cómo podemos identificarlos a partir de sus ecuaciones. 

Circulo

Circunferencia es un conjunto de puntos que equidistan de un punto fijo. 

La siguiente figura representa un círculo cuyo centro está dado por O y el radio es la línea que une el centro con cualquier punto del círculo. 

Su ecuación está dada por, 

(x – h) ² + (y – k) ² = r ²

Donde (h, k) es el centro del círculo, y el radio viene dado por “r”. Esta ecuación se puede reorganizar para traerla en la siguiente forma: 

x ² + y ² -2hx -2kx + h ² + k ²  = r ²

Identificar círculos a partir de sus ecuaciones

Un círculo tendrá cuadrados x e y presentes en su ecuación con coeficientes distintos de cero. Tanto x ² como y ² deben tener el mismo signo. Una vez que sabemos que es una ecuación del círculo, la curva se puede recuperar. 

Por ejemplo:

La ecuación dada es, 4x ² + 4y ² + 7y= 9 , La forma más fácil de identificar cuándo la ecuación dada es la ecuación de un círculo,

1. Ambos cuadrados de x e y están presentes en la ecuación.

2. Los coeficientes de los cuadrados de x e y son iguales (aquí, +4).

Estas dos informaciones indican que la ecuación de la curva proporcionada es un círculo.

Parábola

Una parábola es el conjunto de todos los puntos en un plano que son equidistantes de una línea fija y un punto fijo (no en la línea) en el plano

La línea fija se llama directriz y el punto se llama foco.

Ecuaciones estándar de parábola

La ecuación de una parábola estándar con el eje x como eje, que pasa por el origen y el foco en (a,0) viene dada por, 

y2 ⁼ 4ax

Las siguientes figuras muestran diferentes tipos de parábolas con sus ecuaciones. 

Identificar parábola a partir de sus ecuaciones

Reconocer una ecuación de una parábola a partir de la ecuación expandida. Necesitamos notar solo una cosa. Las ecuaciones de parábola deben tener y o x al cuadrado, pero no ambos. El resto de los valores pueden ser cualquier cosa. Si una ecuación tiene x o y al cuadrado pero no ambos. Luego se puede reorganizar en la forma de una ecuación estándar de una parábola. 

Por ejemplo:

Echa un vistazo a estas ecuaciones,

x2 ⁼ y+ 4, ^y2 – 3x+ 9= 0

Ambas ecuaciones mencionadas anteriormente son una parábola porque,

1. Ambas ecuaciones tienen una de las variables al cuadrado, pero no ambas. Por lo tanto, las ecuaciones son parábolas.

Elipse 

Una elipse es un conjunto de todos los puntos en un plano, la suma de cuyas distancias a dos puntos fijos en un plano es constante. 

Los dos puntos mencionados en la definición anterior se llaman focos de la elipse.

La ecuación estándar de la elipse que tiene el eje x como eje mayor y el eje y como eje menor está dada por, 

Donde, c ² = a ² – b ²

En caso de que la elipse tenga un eje mayor en el eje y y así sucesivamente. Entonces la ecuación está dada por, 

Identificar elipses a partir de su ecuación: Al igual que los círculos, las elipses también tienen cuadrados x e y. Pero la diferencia es que tendrán diferentes coeficientes. 

Por ejemplo:

5x ² + 7y ² – 9x- 6y = 0, 9y ² + 2y ² + 8x+ y= 0

Ambas ecuaciones son las curvas de elipse porque,

1. Ambas variables xey están elevadas al cuadrado.

2. Los coeficientes de ambas variables al cuadrado tienen valores diferentes (si los coeficientes fueran iguales, la curva sería un círculo)

Hipérbola

La hipérbola es un conjunto de puntos en un plano, la diferencia de cuyas distancias a dos puntos fijos en el plano es una constante. 

La ecuación estándar de Hipérbola viene dada por, 

Aquí también, c ² = a ² – b ²

En el caso anterior, el eje transversal es el eje x y el eje conjugado es el eje y. Si se invierten los ejes, la ecuación resultará ser, 

Identificar una hipérbola a partir de su ecuación: Al igual que los círculos, las hipérbolas también tienen cuadrados x e y. Pero la diferencia es que tendrán coeficientes diferentes y los signos serán opuestos. 

Por ejemplo:

5x ² – 2y ² + 7x= 8

La ecuación anterior es la ecuación de una hipérbola ya que,

1. Tanto x como y con un grado 2 presente.

2. una de las variables al cuadrado tiene un signo diferente a la otra, en este caso el coeficiente y ² es negativo y el coeficiente x ² es positivo.

Veamos algunos ejemplos de problemas sobre estos conceptos. 

Problemas de muestra 

Pregunta 1: Identifique la curva a partir de su ecuación expandida. 

y ² -4y + 2 = 12x

Solución: 

y ² – 4y + 2 = 12x

Esta ecuación contiene solo y cuadrado. Hemos visto en las secciones anteriores que las ecuaciones de la parábola tienen x o y al cuadrado. Entonces, esta debe ser la ecuación de la parábola. 

Reordenando la ecuación dada, 

y ² – 4y + 2 = 12x

⇒ y ² – 4y + 4 + 2 – 4 = 12x 

⇒(y – 2) ² – 2 =12x 

⇒(y – 2) ² = 12x + 2 

⇒

Pregunta 2: Identifique la curva a partir de su ecuación expandida: 

4x ² + 9y ² = 36

Solución: 

4x ² + 9y ² = 36

La ecuación dada tiene cuadrados x e y presentes en ella. Ambos tienen coeficientes positivos pero diferentes. Entonces, podría ser una ecuación de elipse. 

Entonces, esta es la ecuación con a = 3 y b = 2. 

Pregunta 3: Identifique la curva a partir de su ecuación expandida: 

7x ² – 9y ² = 36

Solución: 

7x ² – 9y ² = 36

Esta ecuación también tiene cuadrados de x e y, pero los signos son diferentes. Con base en el método mencionado anteriormente, podemos decir que se trata de una hipérbola. 

Ahora necesitamos traer la ecuación expandida en forma estándar. 

Aquí, a =  y b = 2

Pregunta 4: Dada la ecuación expandida de una curva, identifícala y devuélvela a la forma estándar. 

x2 + ^{y2 +}  6y = 27

Solución: 

x2 + ^{y2 +} 6y = 27

Ambos cuadrados x e y están presentes y tienen el mismo signo y 1 como su coeficiente. Esta es una ecuación de un círculo. 

x2 + ^{y2 +} 6y = 27

⇒ x2 + ^{y2 +} 6y + 9 = 27 + 9 

⇒ x ² + (y + 3) ² = 36 

⇒ x ² + (y + 3) ² = 6 ²

Esta es la ecuación de la circunferencia con centro en (0,-3) y radio 6.  

Pregunta 5: Identifique la curva y formule su ecuación a partir de la expresión dada. 

x ² + y ² + 4x + 6x = 12

Solución: 

Tomemos la ecuación dada,

x ² + y ² + 4x + 6x = 12

De las ecuaciones que hemos estudiado anteriormente, observe que en la ecuación dada, x e y, ambos están elevados al cuadrado y ambos tienen el mismo signo y los mismos coeficientes. Como se mencionó anteriormente, las ecuaciones del círculo deben tener cuadrados x e y con el mismo signo y coeficientes. Por lo tanto, esta es la ecuación del círculo. 

Para encontrar el centro y el radio del círculo, necesitamos reorganizarlo. 

x ² + y ² + 4x + 6x = 12

Necesitamos hacer cuadrados enteros con los términos x e y 

x ² + 4x + y ² + 6x = 12

⇒ x2 ⁺ 4x + 4 – 4 + ^y2 + 6x + 9 – 9 = 12

⇒ (x + 2) ² -4 + (y + 3) ² – 9 = 12 

⇒ (x + 2) ² + (y + 3) ² = 12 + 9 + 4 

⇒(x + 2) ² + (y + 3) ² = 25 

⇒(x + 2) ² + (y + 3) ² = 5 ²

Entonces, el centro es (-2,-3) y el radio es 5.