Métodos algebraicos para resolver pares de ecuaciones lineales en dos variables

Imaginemos una situación, Ankita fue a una feria en su pueblo. Quería subirse a atracciones como la Rueda Gigante y jugar Hoopla (un juego en el que se lanza un anillo sobre los artículos guardados en un puesto, y si el anillo cubre cualquier objeto por completo, el jugador lo obtiene). El número de veces que jugó Hoopla es la mitad del número de paseos que tuvo en la rueda gigante. Si cada paseo en la rueda gigante cuesta Rs 3, y un juego de Hoopla cuesta Rs 4, averigüe el número de paseos que tuvo y cuántas veces jugó Hoopla, siempre que gastó Rs 20.

Para resolver este tipo de problema, el primer paso es formularlo en términos de ecuaciones. Sea x el número de veces que Ankita montó en la Rueda Gigante y sea y el número de veces que jugó Hoopla. Las ecuaciones se convierten en,

x = 2y,

3x + 4y = 20.

¿Podemos encontrar la solución a este sistema de ecuaciones? Hay varias formas de encontrar soluciones, veámoslas en detalle.

Par de ecuaciones lineales en dos variables

Una ecuación que se puede poner en la forma de ax + by + c = 0, donde a, b y c son números reales y a y b son distintos de cero se llama ecuación lineal en dos variables x e y. Geométricamente, si todos los puntos que satisfacen esta ecuación se trazan en el plano cartesiano. Representa una línea.

De manera similar, un sistema de dos ecuaciones lineales representa dos líneas. La solución de ese sistema representa puntos que satisfacen ambas ecuaciones. No puede haber ningún punto, un punto e infinitos puntos.

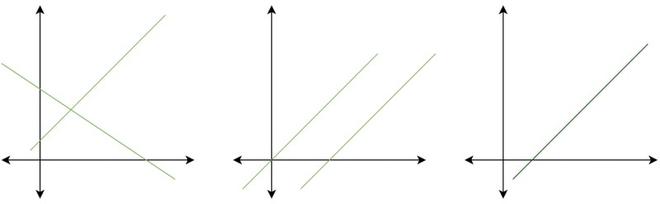
Una solución, ninguna solución e infinitamente muchas soluciones.

Métodos algebraicos para resolver un par de ecuaciones lineales

Hay varios métodos para resolver algebraicamente un sistema de ecuaciones lineales, veamos dos de esos métodos:

Método de sustitución
Método de eliminación

Método de sustitución

Este método implica principalmente dos pasos:

Paso 1: encuentre el valor de una variable, digamos y en términos de la otra variable, es decir, x de cualquier ecuación, cualquiera que sea conveniente.

Paso 2: Sustituir este valor de y en la otra ecuación y reducirlo a una ecuación en una variable, es decir, en términos de x, que se puede resolver.

Pregunta: Resuelve el siguiente sistema de ecuaciones:

7x – 15y = 2

x + 2y = 3

Solución:

Se puede solucionar siguiendo los pasos explicados anteriormente,

Elegimos una ecuación para representar el valor de una variable en términos de otras,

Escojamos, x = 3- 2y (También es conveniente).

Sustituye el valor de x en la otra ecuación.

7(3-2 años) -15 años = 2

⇒ 21 – 14 años -15 años = 2

⇒ 19 = 29 años

⇒ y = 19/29

Ahora, el valor de x se convierte en x = 3 – 2(19/29) = 3 – (38/29) = 49/29

Esta solución también se puede comprobar sustituyendo ambos valores en estas ecuaciones.

Nota: hemos sustituido el valor de una variable expresándolo en términos de otra variable para resolver el problema. Es por eso que este método se llama sustitución.

A veces, como en el Ejemplo a continuación, podemos obtener declaraciones sin variable. Si esta afirmación es cierta, podemos decir que el par de ecuaciones lineales tiene infinitas soluciones. Si la declaración es falsa, entonces el par de ecuaciones lineales es inconsistente.

Pregunta: Anuj y Rahul compraron algunos artículos de papelería en la tienda. Anuj compró 2 lápices y 3 borradores. El costo de 2 lápices y 3 borradores fue de Rs 9 y Rahul compró 4 lápices y 6 borradores. El costo de 4 lápices y 6 borradores es Rs 18. Halla el costo de cada lápiz y cada borrador.

Solución:

El par de ecuaciones lineales que se forma a partir de la descripción anterior es,

2x + 3y = 9

4x + 6y = 18

donde x es el costo de un lápiz y y es el costo de la goma de borrar.

x = $\frac{9 - 3y}{2}$

Poniendo este valor en la otra ecuación.

$4(\frac{9 - 3y}{2}) + 6y = 18 \\ 18 - 6y + 6y = 18 \\ 18 = 18$

Esta afirmación es cierta para todos los valores de y. Sin embargo, no obtenemos un valor específico de y como solución. Por lo tanto, no podemos obtener un valor específico de x. Esta situación ha surgido porque ambas ecuaciones dadas son iguales. Por lo tanto, estas ecuaciones tienen infinitas soluciones.

Método de eliminación

Este método implica principalmente los siguientes pasos:

Multiplique ambas ecuaciones por algunas constantes adecuadas distintas de cero y haga que los coeficientes de una variable (ya sea x o y) sean numéricamente iguales.
Suma o resta una ecuación de la otra para que se elimine una variable. Si se obtiene una ecuación en una variable, vaya al Paso 5.
Si en el Paso 2 obtenemos un enunciado verdadero que no involucra ninguna variable, entonces el par original de ecuaciones tiene infinitas soluciones.
Si en el Paso 2 obtenemos un enunciado falso que no involucra ninguna variable, entonces el par original de ecuaciones no tiene solución, es decir, es inconsistente.
Resuelva la ecuación en una variable (x o y) así obtenida para obtener su valor.
Sustituye este valor de x (o y) en cualquiera de las ecuaciones originales para obtener el valor de la otra variable.

Pregunta 1: Encuentra todas las soluciones posibles del siguiente sistema de ecuaciones usando el método de eliminación.

2x + 3y = 8 – (1)

4x + 6y = 7 – (2)

Solución:

Multiplica la ecuación (1) por 2 y la ecuación (2) por 1. Esto hará que los coeficientes de x en ambas ecuaciones sean iguales. Entonces obtenemos las ecuaciones como:

4x + 6y = 16

4x + 6y = 7

Restando ambas ecuaciones,

obtenemos 0 = 9

esto es falso Entonces, no existe solución para este sistema de ecuaciones lineales.

Pregunta 2: La suma de un número de dos dígitos y el número obtenido al invertir los dígitos es 66. Si los dígitos del número difieren en 2, encuentre el número. ¿Cuántos números de este tipo hay?

Solución:

Sean x e y las cifras de las decenas y las unidades respectivamente. Entonces, el primer número se puede escribir como 10x + y es la forma expandida (por ejemplo, 56 = 10 (6) + 5).

(10x + y) + (10y + x) = 66,

es decir, ⇒ 11(x + y) = 66

es decir, ⇒ x + y = 6

También se da que los dígitos difieren en 2,

Entonces, ya sea x – y = 2 o y – x = 2. Busquemos ambos casos,

Caso 1: x – y = 2,

Sustituyendo x = y + 2 en la ecuación anterior,

y + 2 + y = 6

⇒ 2 años = 4

⇒ y = 2.

Entonces, x = 4

Caso 2: y – x = 2,

Sustituyendo y = x + 2, en la ecuación dada arriba,

x + y = 6.

⇒ x + x + 2 = 6

⇒ 2x = 4

⇒ x = 2

y = 4.

Método de multiplicación cruzada

Es una de las técnicas para determinar la solución de una ecuación lineal en dos variables, se sabe que es el método más rápido.

Supongamos un par de ecuaciones lineales:

un ₁ x + segundo ₁ y + c ₁ = 0

un ₂ x + _{segundo 2} y + c ₂ = 0

Al usar la multiplicación cruzada, podemos encontrar los valores de ‘x’ e ‘y’:

$x=\frac{(b_{1}c_{2})-(b_{2}c_{1})}{(b_{2}a_{1})-(b_{1}a_{2})}\\y=\frac{(c_{1}a_{2})-(c_{2}a_{1})}{(b_{2}a_{1})-(b_{1}a_{2})}$

Derivación para multiplicación cruzada

a ₁ x + b ₁ y + c ₁ = 0 ⇢(1)

a ₂ x + b ₂ y + c ₂ = 0 ⇢(2)

Multiplique con b ₂ en la ecuación (1) y b ₁ en la ecuación (2):

a ₁_{segundo 2} x + segundo _{1 segundo 2 y + c 1} segundo ₂ = 0 _⇢ ( ₃ )

a _{2 segundo}₁ x + segundo ₁ segundo ₂ y + c 2 _segundo 1 ₌ 0 ⇢(4)

Restar la ecuación (4) de la ecuación (3) proporcionará los valores de x e y como,

$x=\frac{(b_{1}c_{2})-(b_{2}c_{1})}{(b_{2}a_{1})-(b_{1}a_{2})}\\y=\frac{(c_{1}a_{2})-(c_{2}a_{1})}{(b_{2}a_{1})-(b_{1}a_{2})}$

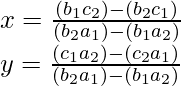
Técnica fácil para entender las fórmulas.

Escriba los coeficientes en forma original:

un ₁ segundo ₁ c ₁

un ₂ b ₂ c ₂

Ignore los coeficientes de x y multiplique en forma cruzada los coeficientes restantes y luego restelos:

Por lo tanto, la solución de la ecuación de la parte uno se convierte en ⇒ $\frac{x}{(b_{1}c_{2})-(b_{2}c_{1})}$

Ahora, ignore el coeficiente de y y multiplique en forma cruzada los términos restantes:

Recuerda considerar la ecuación bajo (-y), La segunda parte de la solución ⇒ $\frac{-y}{(a_{1}c_{2})-(a_{2}c_{1})}$

Para la tercera parte, ignore los coeficientes de 1 y multiplique en cruz los términos restantes y réstelos:

La tercera parte de la ecuación se convierte en ⇒ $\frac{1}{(a_{1}b_{2})-(a_{2}b_{1})}$

Combinando las tres partes ⇒ $\frac{x}{(b_{1}c_{2})-(b_{2}c_{1})}=\frac{-y}{(a_{1}c_{2})-(a_{2}c_{1})}=\frac{1}{(a_{1}b_{2})-(a_{2}b_{1})}$

Pregunta 1: Encuentra el valor de las variables que satisfacen la ecuación usando el método de multiplicación cruzada:

2x + 3y = 11

3x + 2y = 9

Solución:

Escribe ecuaciones en forma general:

2x + 3y – 11 = 0

3x + 2y – 9 = 0

Usando el método de multiplicación cruzada,

$\frac{x}{(b_{1}c_{2})-(b_{2}c_{1})}=\frac{-y}{(a_{1}c_{2})-(a_{2}c_{1})}=\frac{1}{(a_{1}b_{2})-(a_{2}b_{1})}$

Ponga los valores de todos los coeficientes en la fórmula,

$\frac{x}{(3.(-9))-(2.(-11))}=\frac{-y}{(2.(-9))-(3.(-11))}=\frac{1}{(2.2)-(3.3)}$

$\frac{x}{-5}=\frac{-y}{15}=\frac{1}{-5}$

Resolviendo, obtenemos: x=1, y=3

Pregunta 2: usando el método de multiplicación cruzada, resuelve x e y:

3x – 4y – 2 = 0

y-2x-7 = 0

Solución:

Usando la fórmula: $\frac{x}{(b_{1}c_{2})-(b_{2}c_{1})}=\frac{-y}{(a_{1}c_{2})-(a_{2}c_{1})}=\frac{1}{(a_{1}b_{2})-(a_{2}b_{1})}$

Sustituye los valores en la fórmula: $\frac{x}{(-4.(-7))-(-2.(-2))}=\frac{-y}{(3.(-7))-(1.(-2))}=\frac{1}{(3.(-2))-(1.(-4))}$

Resolviendo la ecuación, x=-6, y=-5

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Par de ecuaciones lineales en dos variables

Métodos algebraicos para resolver un par de ecuaciones lineales

Método de sustitución

Método de eliminación

Método de multiplicación cruzada

Derivación para multiplicación cruzada

Deja una respuesta Cancelar la respuesta