Montón de Fibonacci | Serie 1 (Introducción)

Los montones se utilizan principalmente para implementar la cola de prioridad. Hemos discutido a continuación montones en publicaciones anteriores. 

• montón binario 
• Montón binomial 

En términos de Complejidad de tiempo, Fibonacci Heap supera a Binary y Binomial Heaps. 

A continuación se muestran las complejidades del tiempo amortizado de Fibonacci Heap . 

1) Find Min:      Θ(1)     [Same as both Binary and Binomial]
2) Delete Min:    O(Log n) [Θ(Log n) in both Binary and Binomial]
3) Insert:        Θ(1)     [Θ(Log n) in Binary and Θ(1) in Binomial]
4) Decrease-Key:  Θ(1)     [Θ(Log n) in both Binary and Binomial]
5) Merge:         Θ(1)     [Θ(m Log n) or Θ(m+n) in Binary and
                            Θ(Log n) in Binomial]

Al igual que Binomial Heap , Fibonacci Heap es una colección de árboles con propiedades min-heap o max-heap. En Fibonacci Heap, los árboles pueden tener cualquier forma, incluso todos los árboles pueden ser Nodes únicos (esto es diferente a Binomial Heap donde cada árbol tiene que ser Binomial Tree). 

A continuación se muestra un ejemplo de Montón de Fibonacci tomado de aquí . 

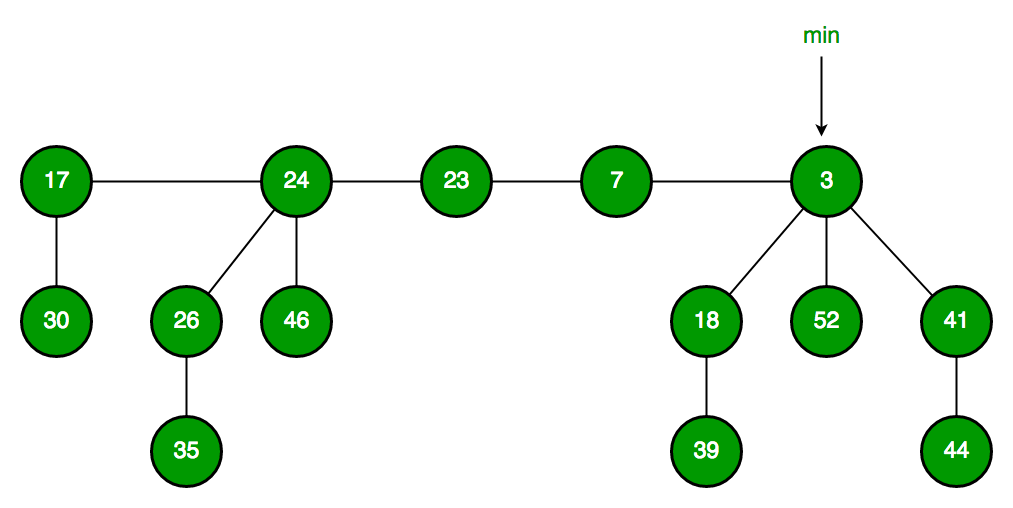
Fibonacci Heap mantiene un puntero al valor mínimo (que es la raíz de un árbol). Todas las raíces de los árboles están conectadas mediante una lista circular doblemente enlazada, por lo que se puede acceder a todas ellas con un solo puntero ‘min’. 

La idea principal es ejecutar operaciones de forma «perezosa». Por ejemplo, la operación de combinación simplemente vincula dos montones, la operación de inserción simplemente agrega un nuevo árbol con un solo Node. La operación extracto mínimo es la operación más complicada. Realiza labores tardías de consolidación de árboles. Esto hace que la eliminación también sea complicada, ya que eliminar primero disminuye la clave a menos infinito, luego llama al mínimo de extracción. 

A continuación se presentan algunos datos interesantes sobre el montón de Fibonacci 

1. La complejidad temporal reducida de Decrease-Key tiene importancia en los algoritmos de Dijkstra y Prim. Con Binary Heap, la complejidad temporal de estos algoritmos es O(VLogV + ELogV). Si se usa Fibonacci Heap, la complejidad del tiempo se mejora a O (VLogV + E)
2. Aunque Fibonacci Heap parece prometedor en cuanto a complejidad de tiempo, se ha encontrado lento en la práctica ya que las constantes ocultas son altas (Fuente Wiki ).
3. El montón de Fibonacci se llama así principalmente porque los números de Fibonacci se utilizan en el análisis del tiempo de ejecución. Además, cada Node en Fibonacci Heap tiene un grado como máximo O(log n) y el tamaño de un subárbol con raíz en un Node de grado k es al menos F k+2 , _donde F _k es el k-ésimo número de Fibonacci.

Pronto discutiremos las operaciones de Fibonacci Heap en detalle. 

Este artículo es una contribución de Shivam . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.