Backtracking es un paradigma algorítmico que prueba diferentes soluciones hasta encontrar una solución que “funciona”. Los problemas que normalmente se resuelven utilizando la técnica de retroceso tienen la siguiente propiedad en común. Estos problemas solo se pueden resolver probando todas las configuraciones posibles y cada configuración se intenta solo una vez. Una solución ingenua para estos problemas es probar todas las configuraciones y generar una configuración que siga las restricciones del problema dado. El retroceso funciona de forma incremental y es una optimización sobre la solución Naive donde se generan y prueban todas las configuraciones posibles.
Por ejemplo, considere el siguiente problema de Knight’s Tour .
Declaración del problema:
dado un tablero N*N con el caballo colocado en el primer bloque de un tablero vacío. Moviéndose de acuerdo con las reglas del ajedrez, el caballero debe visitar cada casilla exactamente una vez. Imprime el orden de cada celda en la que se visitan.
Ejemplo:
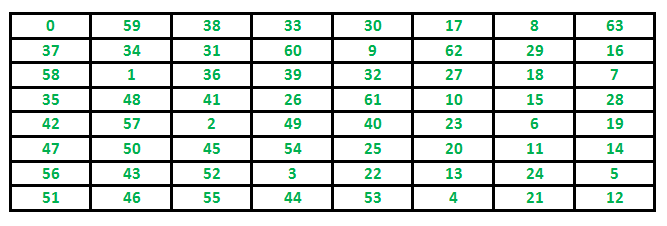
Input : N = 8 Output: 0 59 38 33 30 17 8 63 37 34 31 60 9 62 29 16 58 1 36 39 32 27 18 7 35 48 41 26 61 10 15 28 42 57 2 49 40 23 6 19 47 50 45 54 25 20 11 14 56 43 52 3 22 13 24 5 51 46 55 44 53 4 21 12
El camino seguido por Knight para cubrir todas las celdas
A continuación se muestra un tablero de ajedrez con 8 x 8 celdas. Los números en las celdas indican el número de movimiento del Caballo.
Analicemos primero el algoritmo Naive para este problema y luego el algoritmo Backtracking.
Algoritmo ingenuo para el recorrido de Knight
El algoritmo ingenuo es generar todos los recorridos uno por uno y verificar si el recorrido generado satisface las restricciones.
while there are untried tours
{
generate the next tour
if this tour covers all squares
{
print this path;
}
}
El retroceso funciona de forma incremental para atacar los problemas. Por lo general, comenzamos con un vector de solución vacío y agregamos elementos uno por uno (el significado del elemento varía de un problema a otro. En el contexto del problema del recorrido de Knight, un elemento es un movimiento de Knight). Cuando agregamos un elemento, verificamos si agregar el elemento actual viola la restricción del problema, si lo hace, eliminamos el elemento y probamos otras alternativas. Si ninguna de las alternativas funciona, pasamos a la etapa anterior y eliminamos el elemento agregado en la etapa anterior. Si llegamos a la etapa inicial, decimos que no existe solución. Si agregar un elemento no viola las restricciones, entonces agregamos recursivamente los elementos uno por uno. Si el vector solución se completa, imprimimos la solución.
Algoritmo de retroceso para la gira de Knight
A continuación se muestra el algoritmo de retroceso para el problema del recorrido de Knight.
If all squares are visited
print the solution
Else
a) Add one of the next moves to solution vector and recursively
check if this move leads to a solution. (A Knight can make maximum
eight moves. We choose one of the 8 moves in this step).
b) If the move chosen in the above step doesn't lead to a solution
then remove this move from the solution vector and try other
alternative moves.
c) If none of the alternatives work then return false (Returning false
will remove the previously added item in recursion and if false is
returned by the initial call of recursion then "no solution exists" )
Las siguientes son implementaciones para el problema del recorrido de Knight. Imprime una de las posibles soluciones en forma de array 2D. Básicamente, la salida es una array 2D de 8*8 con números del 0 al 63 y estos números muestran los pasos realizados por Knight.
C++
// C++ program for Knight Tour problem
#include <bits/stdc++.h>
using namespace std;
#define N 8
int solveKTUtil(int x, int y, int movei, int sol[N][N],
int xMove[], int yMove[]);
/* A utility function to check if i,j are
valid indexes for N*N chessboard */
int isSafe(int x, int y, int sol[N][N])
{
return (x >= 0 && x < N && y >= 0 && y < N
&& sol[x][y] == -1);
}
/* A utility function to print
solution matrix sol[N][N] */
void printSolution(int sol[N][N])
{
for (int x = 0; x < N; x++) {
for (int y = 0; y < N; y++)
cout << " " << setw(2) << sol[x][y] << " ";
cout << endl;
}
}
/* This function solves the Knight Tour problem using
Backtracking. This function mainly uses solveKTUtil()
to solve the problem. It returns false if no complete
tour is possible, otherwise return true and prints the
tour.
Please note that there may be more than one solutions,
this function prints one of the feasible solutions. */
int solveKT()
{
int sol[N][N];
/* Initialization of solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x][y] = -1;
/* xMove[] and yMove[] define next move of Knight.
xMove[] is for next value of x coordinate
yMove[] is for next value of y coordinate */
int xMove[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };
int yMove[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };
// Since the Knight is initially at the first block
sol[0][0] = 0;
/* Start from 0,0 and explore all tours using
solveKTUtil() */
if (solveKTUtil(0, 0, 1, sol, xMove, yMove) == 0) {
cout << "Solution does not exist";
return 0;
}
else
printSolution(sol);
return 1;
}
/* A recursive utility function to solve Knight Tour
problem */
int solveKTUtil(int x, int y, int movei, int sol[N][N],
int xMove[8], int yMove[8])
{
int k, next_x, next_y;
if (movei == N * N)
return 1;
/* Try all next moves from
the current coordinate x, y */
for (k = 0; k < 8; k++) {
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol)) {
sol[next_x][next_y] = movei;
if (solveKTUtil(next_x, next_y, movei + 1, sol,
xMove, yMove)
== 1)
return 1;
else
// backtracking
sol[next_x][next_y] = -1;
}
}
return 0;
}
// Driver Code
int main()
{
// Function Call
solveKT();
return 0;
}
// This code is contributed by ShubhamCoder
C
// C program for Knight Tour problem
#include <stdio.h>
#define N 8
int solveKTUtil(int x, int y, int movei, int sol[N][N],
int xMove[], int yMove[]);
/* A utility function to check if i,j are valid indexes
for N*N chessboard */
int isSafe(int x, int y, int sol[N][N])
{
return (x >= 0 && x < N && y >= 0 && y < N
&& sol[x][y] == -1);
}
/* A utility function to print solution matrix sol[N][N] */
void printSolution(int sol[N][N])
{
for (int x = 0; x < N; x++) {
for (int y = 0; y < N; y++)
printf(" %2d ", sol[x][y]);
printf("\n");
}
}
/* This function solves the Knight Tour problem using
Backtracking. This function mainly uses solveKTUtil()
to solve the problem. It returns false if no complete
tour is possible, otherwise return true and prints the
tour.
Please note that there may be more than one solutions,
this function prints one of the feasible solutions. */
int solveKT()
{
int sol[N][N];
/* Initialization of solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x][y] = -1;
/* xMove[] and yMove[] define next move of Knight.
xMove[] is for next value of x coordinate
yMove[] is for next value of y coordinate */
int xMove[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };
int yMove[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };
// Since the Knight is initially at the first block
sol[0][0] = 0;
/* Start from 0,0 and explore all tours using
solveKTUtil() */
if (solveKTUtil(0, 0, 1, sol, xMove, yMove) == 0) {
printf("Solution does not exist");
return 0;
}
else
printSolution(sol);
return 1;
}
/* A recursive utility function to solve Knight Tour
problem */
int solveKTUtil(int x, int y, int movei, int sol[N][N],
int xMove[N], int yMove[N])
{
int k, next_x, next_y;
if (movei == N * N)
return 1;
/* Try all next moves from the current coordinate x, y
*/
for (k = 0; k < 8; k++) {
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol)) {
sol[next_x][next_y] = movei;
if (solveKTUtil(next_x, next_y, movei + 1, sol,
xMove, yMove)
== 1)
return 1;
else
sol[next_x][next_y] = -1; // backtracking
}
}
return 0;
}
/* Driver Code */
int main()
{
// Function Call
solveKT();
return 0;
}
Java
// Java program for Knight Tour problem
class KnightTour {
static int N = 8;
/* A utility function to check if i,j are
valid indexes for N*N chessboard */
static boolean isSafe(int x, int y, int sol[][])
{
return (x >= 0 && x < N && y >= 0 && y < N
&& sol[x][y] == -1);
}
/* A utility function to print solution
matrix sol[N][N] */
static void printSolution(int sol[][])
{
for (int x = 0; x < N; x++) {
for (int y = 0; y < N; y++)
System.out.print(sol[x][y] + " ");
System.out.println();
}
}
/* This function solves the Knight Tour problem
using Backtracking. This function mainly
uses solveKTUtil() to solve the problem. It
returns false if no complete tour is possible,
otherwise return true and prints the tour.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions. */
static boolean solveKT()
{
int sol[][] = new int[8][8];
/* Initialization of solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x][y] = -1;
/* xMove[] and yMove[] define next move of Knight.
xMove[] is for next value of x coordinate
yMove[] is for next value of y coordinate */
int xMove[] = { 2, 1, -1, -2, -2, -1, 1, 2 };
int yMove[] = { 1, 2, 2, 1, -1, -2, -2, -1 };
// Since the Knight is initially at the first block
sol[0][0] = 0;
/* Start from 0,0 and explore all tours using
solveKTUtil() */
if (!solveKTUtil(0, 0, 1, sol, xMove, yMove)) {
System.out.println("Solution does not exist");
return false;
}
else
printSolution(sol);
return true;
}
/* A recursive utility function to solve Knight
Tour problem */
static boolean solveKTUtil(int x, int y, int movei,
int sol[][], int xMove[],
int yMove[])
{
int k, next_x, next_y;
if (movei == N * N)
return true;
/* Try all next moves from the current coordinate
x, y */
for (k = 0; k < 8; k++) {
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol)) {
sol[next_x][next_y] = movei;
if (solveKTUtil(next_x, next_y, movei + 1,
sol, xMove, yMove))
return true;
else
sol[next_x][next_y]
= -1; // backtracking
}
}
return false;
}
/* Driver Code */
public static void main(String args[])
{
// Function Call
solveKT();
}
}
// This code is contributed by Abhishek Shankhadhar
Python3
# Python3 program to solve Knight Tour problem using Backtracking
# Chessboard Size
n = 8
def isSafe(x, y, board):
'''
A utility function to check if i,j are valid indexes
for N*N chessboard
'''
if(x >= 0 and y >= 0 and x < n and y < n and board[x][y] == -1):
return True
return False
def printSolution(n, board):
'''
A utility function to print Chessboard matrix
'''
for i in range(n):
for j in range(n):
print(board[i][j], end=' ')
print()
def solveKT(n):
'''
This function solves the Knight Tour problem using
Backtracking. This function mainly uses solveKTUtil()
to solve the problem. It returns false if no complete
tour is possible, otherwise return true and prints the
tour.
Please note that there may be more than one solutions,
this function prints one of the feasible solutions.
'''
# Initialization of Board matrix
board = [[-1 for i in range(n)]for i in range(n)]
# move_x and move_y define next move of Knight.
# move_x is for next value of x coordinate
# move_y is for next value of y coordinate
move_x = [2, 1, -1, -2, -2, -1, 1, 2]
move_y = [1, 2, 2, 1, -1, -2, -2, -1]
# Since the Knight is initially at the first block
board[0][0] = 0
# Step counter for knight's position
pos = 1
# Checking if solution exists or not
if(not solveKTUtil(n, board, 0, 0, move_x, move_y, pos)):
print("Solution does not exist")
else:
printSolution(n, board)
def solveKTUtil(n, board, curr_x, curr_y, move_x, move_y, pos):
'''
A recursive utility function to solve Knight Tour
problem
'''
if(pos == n**2):
return True
# Try all next moves from the current coordinate x, y
for i in range(8):
new_x = curr_x + move_x[i]
new_y = curr_y + move_y[i]
if(isSafe(new_x, new_y, board)):
board[new_x][new_y] = pos
if(solveKTUtil(n, board, new_x, new_y, move_x, move_y, pos+1)):
return True
# Backtracking
board[new_x][new_y] = -1
return False
# Driver Code
if __name__ == "__main__":
# Function Call
solveKT(n)
# This code is contributed by AAKASH PAL
C#
// C# program for
// Knight Tour problem
using System;
class GFG {
static int N = 8;
/* A utility function to
check if i,j are valid
indexes for N*N chessboard */
static bool isSafe(int x, int y, int[, ] sol)
{
return (x >= 0 && x < N && y >= 0 && y < N
&& sol[x, y] == -1);
}
/* A utility function to
print solution matrix sol[N][N] */
static void printSolution(int[, ] sol)
{
for (int x = 0; x < N; x++) {
for (int y = 0; y < N; y++)
Console.Write(sol[x, y] + " ");
Console.WriteLine();
}
}
/* This function solves the
Knight Tour problem using
Backtracking. This function
mainly uses solveKTUtil() to
solve the problem. It returns
false if no complete tour is
possible, otherwise return true
and prints the tour. Please note
that there may be more than one
solutions, this function prints
one of the feasible solutions. */
static bool solveKT()
{
int[, ] sol = new int[8, 8];
/* Initialization of
solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x, y] = -1;
/* xMove[] and yMove[] define
next move of Knight.
xMove[] is for next
value of x coordinate
yMove[] is for next
value of y coordinate */
int[] xMove = { 2, 1, -1, -2, -2, -1, 1, 2 };
int[] yMove = { 1, 2, 2, 1, -1, -2, -2, -1 };
// Since the Knight is
// initially at the first block
sol[0, 0] = 0;
/* Start from 0,0 and explore
all tours using solveKTUtil() */
if (!solveKTUtil(0, 0, 1, sol, xMove, yMove)) {
Console.WriteLine("Solution does "
+ "not exist");
return false;
}
else
printSolution(sol);
return true;
}
/* A recursive utility function
to solve Knight Tour problem */
static bool solveKTUtil(int x, int y, int movei,
int[, ] sol, int[] xMove,
int[] yMove)
{
int k, next_x, next_y;
if (movei == N * N)
return true;
/* Try all next moves from
the current coordinate x, y */
for (k = 0; k < 8; k++) {
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol)) {
sol[next_x, next_y] = movei;
if (solveKTUtil(next_x, next_y, movei + 1,
sol, xMove, yMove))
return true;
else
// backtracking
sol[next_x, next_y] = -1;
}
}
return false;
}
// Driver Code
public static void Main()
{
// Function Call
solveKT();
}
}
// This code is contributed by mits.
Javascript
<script>
// Javascript program for Knight Tour problem
let N = 8;
// A utility function to check if i,j are
// valid indexes for N*N chessboard
function isSafe(x, y, sol)
{
return(x >= 0 && x < N && y >= 0 &&
y < N && sol[x][y] == -1);
}
// A utility function to print solution
// matrix sol[N][N]
function printSolution(sol)
{
for(let x = 0; x < N; x++)
{
for(let y = 0; y < N; y++)
document.write(sol[x][y] + " ");
document.write("<br/>");
}
}
// This function solves the Knight Tour problem
// using Backtracking. This function mainly
// uses solveKTUtil() to solve the problem. It
// returns false if no complete tour is possible,
// otherwise return true and prints the tour.
// Please note that there may be more than one
// solutions, this function prints one of the
// feasible solutions.
function solveKT()
{
let sol = new Array(8);
for(var i = 0; i < sol.length; i++)
{
sol[i] = new Array(2);
}
// Initialization of solution matrix
for(let x = 0; x < N; x++)
for(let y = 0; y < N; y++)
sol[x][y] = -1;
// xMove[] and yMove[] define next move of Knight.
// xMove[] is for next value of x coordinate
// yMove[] is for next value of y coordinate
let xMove = [ 2, 1, -1, -2, -2, -1, 1, 2 ];
let yMove = [ 1, 2, 2, 1, -1, -2, -2, -1 ];
// Since the Knight is initially at the first block
sol[0][0] = 0;
// Start from 0,0 and explore all tours using
// solveKTUtil()
if (!solveKTUtil(0, 0, 1, sol, xMove, yMove))
{
document.write("Solution does not exist");
return false;
}
else
printSolution(sol);
return true;
}
// A recursive utility function to solve Knight
// Tour problem
function solveKTUtil(x, y, movei, sol, xMove, yMove)
{
let k, next_x, next_y;
if (movei == N * N)
return true;
// Try all next moves from the
// current coordinate x, y
for(k = 0; k < 8; k++)
{
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol))
{
sol[next_x][next_y] = movei;
if (solveKTUtil(next_x, next_y, movei + 1,
sol, xMove, yMove))
return true;
else
sol[next_x][next_y] = -1; // backtracking
}
}
return false;
}
// Driver code
// Function Call
solveKT();
// This code is contributed by target_2
</script>
0 59 38 33 30 17 8 63 37 34 31 60 9 62 29 16 58 1 36 39 32 27 18 7 35 48 41 26 61 10 15 28 42 57 2 49 40 23 6 19 47 50 45 54 25 20 11 14 56 43 52 3 22 13 24 5 51 46 55 44 53 4 21 12
Complejidad de tiempo:
hay N 2 celdas y para cada una, tenemos un máximo de 8 movimientos posibles para elegir, por lo que el peor tiempo de ejecución es O (8 N ^ 2 ).
Espacio Auxiliar: O(N 2 )
Nota importante:
No hay orden de xMove, yMove es incorrecto, pero afectará drásticamente el tiempo de ejecución del algoritmo. Por ejemplo, piense en el caso en el que la octava opción del movimiento es la correcta, y antes de eso, nuestro código ejecutó 7 rutas incorrectas diferentes. Siempre es una buena idea tener una heurística que intentar retroceder aleatoriamente. Como, en este caso, sabemos que el siguiente paso probablemente sea en dirección sur o este, entonces verificar los caminos que conducen al primero es una mejor estrategia.
Tenga en cuenta que Retroceder no es la mejor solución para el problema del recorrido del Caballero. Consulte el siguiente artículo para conocer otras mejores soluciones. El propósito de esta publicación es explicar Backtracking con un ejemplo.
Algoritmo de Warnsdorff para el problema del recorrido de Knight
Referencias:
http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf
http://www.cis.upenn.edu/~matuszek/cit594-2009/Lectures/35-backtracking.ppt
http:/ /mathworld.wolfram.com/KnightsTour.html
http://en.wikipedia.org/wiki/Knight%27s_tour
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA