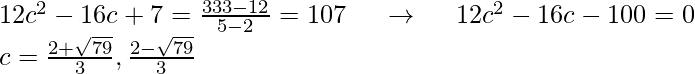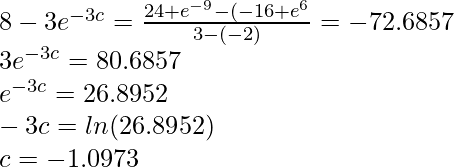Teorema del valor medio de Rolle y Lagrange

Teoremas del valor medio (MVT) es uno de los teoremas que aparecen con frecuencia en la literatura de educación matemática. Es una de las herramientas más importantes utilizadas para probar muchos otros teoremas en cálculo diferencial e integral. A veces se enseña con su caso especial, el teorema de Rolle. El teorema de Rolle lleva el nombre de Michel Rolle (1652-1719), un matemático francés que estableció el símbolo ahora común para la raíz n-ésima e insistió en que -a > -b, para a y b positivas, a < b. La hazaña fue en contra de las enseñanzas de Descartes y sentó las bases para la introducción de la omnipresente recta numérica.

Teorema de Rolle

Establece que si y = f(x) y se da un intervalo [a, b] y que cumple las siguientes condiciones:

1. f(x) es continua en [a, b].
2. f(x) es diferenciable en (a, b).
3. f(a) = f(b)

Entonces existe al menos un número real c ∈ (a, b) tal que f'(c) = 0.

Nota: No es necesario que el inverso de este teorema también sea cierto. Es decir, no podemos decir que si en algún punto f'(c) = 0 se cumplen todas las condiciones del teorema de Rolle. 

Prueba del teorema de Rolle

Sea k = f(a) = f(b). Consideramos tres casos:

1. f(x) = k para todo x ∈ (a, b).
2. Existe un x ∈ (a, b) tal que f(x) > k.
3. Existe un x ∈ (a, b) tal que f(x) < k.

Caso 1: Si f(x) = k para todo x ∈ (a, b), entonces f'(x) = 0 para todo x ∈ (a, b).

Caso 2: Dado que f es una función continua en el intervalo cerrado y acotado [a, b], por el teorema del valor extremo, tiene un máximo absoluto. Además, como existe un punto x ∈ (a, b) tal que f(x) > k, el máximo absoluto es mayor que k. Por lo tanto, el máximo absoluto no ocurre en ningún punto final. Como resultado, el máximo absoluto debe ocurrir en un punto interior xc∈ (a, b). Como f tiene un máximo en un punto interior c, yf es diferenciable en c, por el teorema de Fermat, f'(c)=0.

Caso 3: El caso cuando existe un punto x ∈ (a, b) tal que f(x) < k es análogo al caso 2, con el máximo reemplazado por el mínimo.

Problemas de muestra

Pregunta 1: Determine todos los puntos ‘c’ que satisfacen el teorema de Rolle para f(x) = x ² – 2x – 8 en [-1, 3].

Solución:

Antes de encontrar los puntos, debemos asegurarnos de que todas las condiciones del teorema de Rolle se aplican en este intervalo. Esta función es un polinomio, por lo que es diferenciable y continua en el intervalo. Ahora vamos a evaluar la función en los extremos del intervalo. f(-1) = -5 y f(3) = -5. Los valores de la función son iguales en ambos extremos. Entonces, ahora se cumplen todas las condiciones para el teorema de Rolle.

f'(x) = 2x – 2.

f'(x) = 2x – 2 = 0.

      = x = 1

Entonces, c = 1. 

Pregunta 2: Determine todos los puntos ‘c’ que satisfacen el teorema de Rolle para f(x) = 2x- x ² – x ³ en el intervalo [-2, 1]. 

Solución:

Esta función también es un polinomio, por lo que es tanto diferencial como continua en el intervalo. Valores al final del intervalo f(-2) = 0 = f(1).

Entonces, el teorema de Rolle es aplicable aquí.

f'(x) = 2 – 2x – 3x ²

Para encontrar los puntos como ‘c’

f'(x) = 0

⇒ 2 – 2x – 3x ² = 0

⇒ 3x ² + 2x -2 = 0

Aplicando la fórmula cuadrática de Shree Dharacharya para encontrar los valores de c, 

Entonces, aquí hay dos valores que satisfacen el teorema de Rolle. 

Pregunta 3: Examinar si el teorema de rolle es aplicable para las funciones f(x) = [x] para x ∈ [5, 9]. 

Solución:

Esta función es una función escalonada, no es continua. Entonces, el teorema de Rolle no es aplicable en el siguiente intervalo. 

f(x) = [x]

Teorema del valor medio

Es uno de los teoremas más importantes del cálculo. Establece que si y = f(x) y se da un intervalo [a, b] y que cumple las siguientes condiciones: 

• f(x) es continua en [a, b].
• f(x) es diferenciable en (a, b).

Entonces existe al menos un número c ∈ (a, b) tal que 

Hablando geométricamente, la derivada en c denota la pendiente de la tangente de en x = c para f(x). Dice que debe existir un punto entre ese intervalo donde la pendiente de la tangente sea igual a la pendiente de la línea que une los puntos x = a y x = b. 

Nota: Puede haber cualquier número de puntos c. El teorema del valor medio también se llama primer teorema del valor medio.

Prueba: 

Sea “f” la que satisfaga las hipótesis de la MVT en el intervalo [a, b]. Definir  _ Esto representa la línea secante entre a y b. 

Caso 1: g alcanza su máximo y mínimo en ay b. Entonces “g” es constante. En este caso obtenemos   en cada punto en [a, b]

Caso 2: Si se alcanza el máximo o el mínimo en un punto interior c, entonces g'(c)=0. Por lo tanto, 

Interpretación física del teorema del valor medio

Se sabe que en el Teorema del Valor Medio,  es el cambio promedio en la función sobre [a, b], y f'(c) es el cambio instantáneo en ‘c’. Establece que el cambio instantáneo sobre el intervalo es igual al cambio promedio de la función en algún punto interior. 

Aplicación del teorema del valor medio

Se sabe que el teorema del valor medio es uno de los teoremas más esenciales en el análisis y, por lo tanto, todas sus aplicaciones tienen una gran importancia. Algunas de las aplicaciones se enumeran a continuación:

• Regla de Leibniz.
• Regla de L’Hospital.
• Funciones estrictamente crecientes y estrictamente decrecientes.
• La simetría de las Segundas derivadas.
• La función es constante si f: (a, b)  R es Diferenciable y f'(x)=0 para todo x\in(a, b).

Problemas de muestra

Pregunta 1: Determine todos los números “c” que satisfacen la conclusión del Teorema del Valor Medio para h(z) = 4z ³ – 8z ² + 7z – 2 en [2,5]. 

Solución:

Dado que la función es un polinomio, entonces es continua y diferenciable tanto en este intervalo. Por lo tanto, el teorema del valor medio se puede aplicar aquí. 

h(2) = 12 y h(5) = 333 y h'(z) = 12z ² -16z + 7

Ahora inserte esto en la fórmula del teorema del valor medio y resuelva para c. 

Pregunta 2: f(x) =  . Encuentre el intervalo sobre el cual se puede aplicar el teorema del valor medio. 

Solución:

f(x) no está definida en x = 0. Entonces, x = 0 no está en el dominio si f(x). 

Dado que MVT solo se puede definir en lugares donde f(x) es diferenciable y continua. Se puede definir (-∞, 0) y (0,∞). 

Pregunta 3: Determinar todos los números “c” que satisfacen la conclusión del Teorema del Valor Medio en el intervalo [-2,2] para f(x) = 

Solución:

La función dada, f(x) =|x – 2| + |x| no es diferenciable. Por lo tanto, el teorema del valor medio no se puede aplicar a esta función en el intervalo [-2, 2]. 

Gráfica de la función dada. 

Pregunta 4: Determine todos los números “c” que satisfacen la conclusión del Teorema del valor medio en el intervalo para   [-2,3].

Solución:

Esta función es una suma de funciones exponenciales y polinómicas. Dado que ambas funciones son continuas y diferenciables en todas partes, la función f(t) es continua y derivable en todas partes. Por lo tanto, el teorema del valor medio es aplicable. 

f(-2) = -16 + e ^{(-3 .-2)} = -16 + e ⁶ , f(3) = 24 + e ^-9 y f'(t) = 8 -3e ^-3t . 

Vamos a conectarlo a la fórmula, 

Este es el valor de c.