En matemáticas, como sabemos, una función es una relación entre la entrada y la salida. Una función puede ser creciente, decreciente o constante para los intervalos dados en todo su dominio, y son continuas y derivables en el intervalo dado. Ahora, qué es un intervalo: entonces, un intervalo se conoce como una parte o porción continua o conexa en la línea real. Esta función creciente o decreciente se usa generalmente en la aplicación de derivadas. Entonces, si desea encontrar que la función dada es creciente o decreciente en el intervalo dado, puede encontrarla fácilmente con la ayuda de derivadas.
¿Qué es una función creciente, decreciente y constante?
Función creciente: cuando una función crece en el intervalo dado, este tipo de función se conoce como función creciente. O en otras palabras, cuando una función, f(x), es creciente, los valores de f(x) son crecientes a medida que x crece. O bien, consideremos que I es un intervalo que se presenta en el dominio de una función de valor real f. Entonces la función f es creciente en I, si x1 < x2 en I ⇒ f(x1) < f(x2) ∀ x1, x2 ∈ I. O, en términos de derivada, una función es creciente cuando la derivada en ese punto es positivo. La representación gráfica de una función creciente es:

Función decreciente: cuando una función es decreciente en el intervalo dado, este tipo de función se conoce como función decreciente. O, en otras palabras, cuando una función, f(x), es decreciente, los valores de f(x) son decrecientes a medida que x aumenta. O bien, consideremos que I es un intervalo que se presenta en el dominio de una función de valor real f. Después
- La función f es decreciente en I, si x1, x2 en I ⇒ f(x1) < f(x2) ∀ x1, x2 ∈ I.
- La función f es decreciente en I, si x1 < x2 en I ⇒ f (x1) ≥ f(x2)∀ x1, x2 ∈ I.
- La función f es estrictamente decreciente en I, si x1 < x2 en I ⇒ f(x1) > f(x2)∀ x1, x2 ∈ I.
O, en términos de derivada, una función es decreciente cuando la derivada en ese punto es negativa. La representación gráfica de una función decreciente es:

Función constante: cuando una función no es ni creciente ni decreciente en el intervalo dado, este tipo de función se conoce como función constante. O en otras palabras, cuando una función, f(x), es constante, el valor de f(x) no cambia a medida que x aumenta. O, consideremos que soy un intervalo que se presenta en el dominio de una función de valor real F. Entonces la función f es constante en I, si f(x) = c ∀ x ∈ I. Aquí, c es una constante. O, en términos de derivada, una función es constante (es decir, ni creciente ni decreciente) cuando la derivada es cero. La representación gráfica de la función constante es:

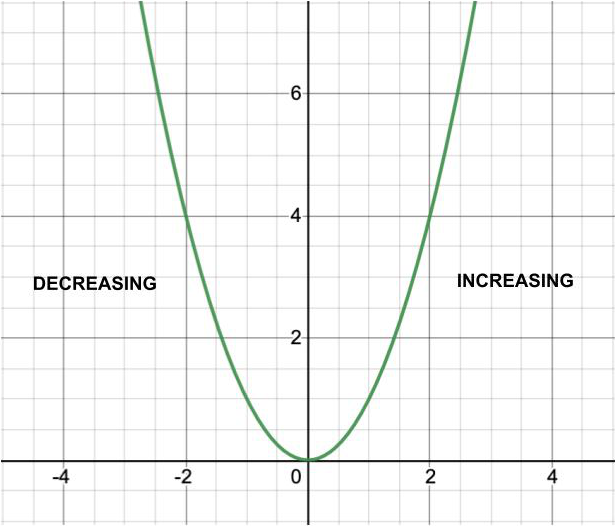
Ejemplo: En este ejemplo, investigaremos la gráfica de f(x) = x 2 .
Mesa:
X f(x) -4 dieciséis -3 9 -2 4 -1 1 0 0 1 1 2 4 3 9 4 dieciséis Como podemos ver, cuando x < 0, el valor de f(x) disminuye a medida que la gráfica se mueve hacia la derecha. En otras palabras, la «altura» del gráfico se está haciendo más pequeña. Esto también se confirma mirando la tabla de valores. Cuando x < 0, a medida que x aumenta, f(x) disminuye. Por lo tanto, f(x) es decreciente en el intervalo desde menos infinito hasta 0.
Cuando x > 0, sucede lo contrario. Cuando x > 0, el valor de f(x) aumenta a medida que la gráfica se mueve hacia la derecha. En otras palabras, la “altura” del gráfico es cada vez más grande. Esto también se confirma mirando la tabla de valores. Cuando x > 0, a medida que x aumenta, f(x) aumenta. Por lo tanto, f(x) es creciente en el intervalo de 0 a infinito.
Propiedades de los intervalos crecientes y decrecientes
Algunas propiedades algebraicas útiles:
- Propiedad aditiva. Si la función f y g son crecientes/decrecientes en el intervalo (a, b), entonces la suma de las funciones f + g también es creciente/decreciente en este intervalo.
- Propiedad opuesta. Si la función f es creciente/decreciente en el intervalo (a, b), entonces la función opuesta, -f, es decreciente/creciente.
- Propiedad inversa. Si la función f es creciente/decreciente en el intervalo (a, b), entonces la función inversa, 1/f, es decreciente/creciente en este intervalo.
- Propiedad multiplicativa. Si las funciones f y g son crecientes/decrecientes y no negativas en el intervalo (a, b), entonces el producto de las funciones también es creciente/decreciente.
Teorema:
Consideremos f como una función continua en el intervalo [p, q] y derivable en el intervalo abierto (p, q), Entonces
- La función f es creciente en [p, q] si f′(x) > 0 para cada x ∈ (p, q).
- La función f es decreciente en [p, q] si f′(x) < 0 para cada x ∈ (p, q)
- La función f es constante en [p, q] si f′(x) = 0 para cada x ∈ (p, q)
O
Una función y = f(x) es creciente en el intervalo (p, q) si y sólo si la primera derivada de la función es positiva para todo x en el intervalo p < x < q.
De manera similar, una función y = f(x) es decreciente en el intervalo (p, q) si y solo si la primera derivada de la función es negativa para todo x en el intervalo p < x < q.
Encuentra intervalos crecientes y decrecientes
Dada una función, f(x), podemos determinar los intervalos donde crece y decrece usando diferenciación y álgebra.
Paso 1: Encuentra la derivada, f'(x), de la función.
Paso 2: Encuentra los ceros de f'(x). Recuerde, los ceros son los valores de x para los cuales f'(x) = 0. Establezca f'(x) = 0 y resuelva para x.
Paso 3: Determinar los intervalos. Los intervalos están entre los extremos del intervalo de f(x) y los ceros de f'(x). Si no se proporciona el intervalo de f(x), suponga que f(x) está en el intervalo (-∞, ∞).
Paso 4: determina si la función es creciente o decreciente en cada intervalo. Dado el intervalo (a, c), elija un valor b, a < b < c. Resuelva para f'(b). Si f'(b) es positiva, f(x) crece en (a, c). Si f'(b) es negativa, f(x) es decreciente en (a, c).
Ejemplo 1:
Si g(x) = (x – 5) 2 , encuentre los intervalos donde g(x) crece y decrece.
Paso 1: Encuentra la derivada de la función.
Usando la regla de la string,
g'(x) = 2(5 – x)
Paso 2: Encuentra los ceros de la función derivada. En otras palabras, encuentra los valores de para los cuales g(x) es igual a cero. Puedes hacer esto estableciendo g(x) = 0 y usando álgebra para resolver x. De las definiciones anteriores, sabemos que la función es constante en los puntos donde la derivada es cero.
g'(x) = 0 = 2(5 – x)
0 = 5 – x
x = 5
Paso 3: Usa los ceros para determinar los intervalos.
Dado que x = 5 es el único cero para g'(x), solo hay 2 intervalos: desde infinito negativo hasta 5, y desde 5 hasta infinito negativo.
Estos se pueden denotar en notación de desigualdad:
-∞ < X < 5
5 < X < ∞
O en notación de intervalo:
(-∞, 5)
(5, ∞)
Recuerda, los extremos NO son inclusivos porque g(x) no crece ni decrece en los extremos.
Paso 4: Determinar si la función es creciente o decreciente en cada intervalo.
Para el primer intervalo, ((-∞, 5), elegiremos b = 0. -∞ < x < 5
g'(b) = g'(0) = 2(5-0) = 10
10 > 0 POSITIVO
Para el segundo intervalo, (5, ∞), elegiremos b = 6. 5 < 6 < ∞
g'(b) = g'(6) = 2(5-6) = -2
-2 < 0 NEGATIVO
Por lo tanto, g(x) es creciente en (-∞, 5) y decreciente en (5, ∞). Podemos verificar nuestros resultados visualmente. En el siguiente gráfico, puedes ver claramente que f(x) = (x – 5) 2 es creciente en el intervalo (5, ∞) y decreciente en el intervalo (-∞, 5).
Podemos verificar visualmente nuestro resultado investigando la gráfica de g(x).
Mirando el gráfico, g(x) de hecho aumenta en el intervalo desde menos infinito hasta 5 y disminuye en el intervalo desde 5 hasta infinito.
Ejemplo 2: Encuentra los intervalos en -20 < x < 20 donde g(x) crece y decrece dado g'(x) = x 2 – 100.
Si se da la derivada, podemos omitir el primer paso e ir directamente a encontrar los ceros.
g'(x)= 0 = x 2 – 100
× 2 = 100
Intervalos: (-20, -10), (-10, 10), (10, 20)
Para (-20, -10), elegiremos b = -12. -20 < -12 < -10
g'(-12) = 44 > 0
Para (-10, 10), elegiremos b = 0. -10 < 0 < 10
g(0) = -100 < 0
Para (10, 20), elegiremos b = 12. 10 < 12 < 20
g(12) = 44 > 0
Por lo tanto, para -20 < x < 20, g(x) crece en (-20, -10) y (10, 20) y disminuye en (-10, 10).
Podemos encontrar g(x) integrando el g'(x) dado. Así,
. Mirando el gráfico, g(x) de hecho aumenta en el intervalo de -20 a -10 y el intervalo de 10 a 20 y disminuye en el intervalo de -10 a 10.
Problemas de muestra
Pregunta 1. Dada la función g(x) = 3x 2 – 12, encuentre los intervalos en -3 < x < 3 donde g(x) es creciente y decreciente.
Solución:
Función dada: g(x) = 3x 2 – 12
Diferenciar wrt x, obtenemos
g'(x) = 6x
Para aumentar y disminuir
Ponga g'(x) = 0
g'(x) = 6x = 0
Entonces, x = 0
Intervalos: (-3, 0), (0, 3)
En x = -2, g'(-2) = -12 < 0
En x = 2, g'(2) = 12 > 0
Entonces, para -3 < x < 3, g(x) decrece en (-3, 0) y aumenta en (0, 3).
Pregunta 2. Dada la derivada de f(x), f'(x) = -10x 2 + 40x, encuentre los intervalos donde f(x) es creciente y decreciente.
Solución:
Dado: f'(x) = -10x 2 + 40x
Para aumentar y disminuir
Pon f'(x) = 0
f'(x) = -10x 2 + 40x = 0
Entonces, x = 4, 0
Intervalos: (−∞, 0), (0, 4), (4, ∞)
Entonces, en x = -1, f'(-1) = -50 < 0
en x = 1, f'(1) = 30 > 0
en x = 5, f'(5) = -50 < 0
Entonces, f(x) es creciente en (0, 4) y decreciente en (−∞, 0), (4, ∞)
Pregunta 3. Dada la función g(x) = 5x 2 – 20x + 100, encuentra los intervalos donde g(x) crece y decrece.
Solución:
Dado: g(x) = 5x 2 – 20x + 100
Diferenciar wrt x, obtenemos
g'(x) = 10x – 20
Para aumentar y disminuir
Ponga g'(x) = 0
g'(x) = 10x – 20 = 0
x = 2
Intervalos: (−∞, 2), (2, ∞)
En, x = 1, g'(1) = -10 < 0
En x = 3, g'(3) = 10 > 0
Entonces, g(x) es decreciente en (-∞, 2) y creciente en (2, ∞)
Pregunta 4. Dada la función s(x) = 6x 3 – x 2 , encuentre los intervalos en 0 < x < 10 donde s(x) es creciente y decreciente.
Solución:
Dado: s(x) = 6x 3 – x 2
Diferenciar wrt x, obtenemos
s'(x) = 18x 2 – 2x
Para aumentar y disminuir
Ponga s'(x) = 0
s'(x) = 18x 2 – 2x = 0
x = 1/9, -1/9
Intervalos: (0, 1/9)
Aquí, -1/9 no está en el intervalo dado, 0 < x < 10
Entonces, g'(1/10) = -0.02 < 0
Por lo tanto, para 0 < x < 10, g(x) es decreciente en (0, 1/9)
Pregunta 5. Dado g'(x) = 7x 2 – 8, encuentra los intervalos donde g(x) crece y decrece.
Solución:
Dado: g'(x) = 7x 2 – 8
Para aumentar y disminuir
Ponga g'(x) = 0
g'(x) = 7x 2 – 8 = 0
x =
Intervalos:
Entonces, en x = -10, g'(-10) = 692 > 0
En x = 0, g'(0) = -8 < 0
En x = 10, g'(10) = 692 < 0
Por tanto, g(x) es creciente en
y
, y decreciente en