Toda función matemática, desde la más simple hasta la más compleja, tiene una inversa. En matemáticas, inverso generalmente significa lo contrario. Además, la inversa es la resta. Para la multiplicación, es la división. De la misma manera para las funciones trigonométricas, son las funciones trigonométricas inversas. Las funciones trigonométricas son las funciones de un ángulo. El término función se usa para describir la relación entre dos conjuntos de números o variables. En las matemáticas modernas, existen seis funciones trigonométricas básicas: seno, coseno, tangente, secante, cosecante y cotangente . El inverso de estas funciones es el seno inverso, el coseno inverso, la tangente inversa, la secante inversa, la cosecante inversa y la cotangente inversa. Las funciones trigonométricas son muchas a una funciónpero sabemos que la inversa de una función existe si la función es biyectiva (uno-uno sobre) . Entonces, si restringimos el dominio de las funciones trigonométricas, estas funciones se vuelven biyectivas y el inverso de las funciones trigonométricas se define dentro del dominio restringido.
Nota: El inverso de f se denota por «f -1 « .
Dominio y rango de funciones trigonométricas inversas
Los elementos de X se denominan dominio de f y los elementos de Y se denominan dominio de f. Las imágenes del elemento de X se denominan cuyo rango es un subconjunto de Y. La siguiente imagen demuestra el dominio, el codominio y el rango de la función.

A continuación se muestra la tabla de dominio y rango de funciones trigonométricas inversas:
|
Función |
Dominio |
Rango |
|---|---|---|
| pecado -1 x | [-1, 1] | [-pi/2, pi/2] |
| porque -1 x | [-1, 1] | [0, pi] |
| bronceado -1x _ | R | [-pi/2, pi/2] |
| cuna -1x _ | R | (0, pi) |
| segundo -1 x | R-(-1,1) | [0, pi], {pi/2} |
| cosec -1 x | R-(-1,1) | [-pi/2, pi/2] – {0} |
Derivadas de funciones trigonométricas inversas usando el primer principio
Entendamos este tema tomando algunos problemas, los cuales resolveremos usando el Primer Principal.
Declaración del problema: sen -1 x = y, bajo condiciones dadas -1 ≤ x ≤ 1, -pi/2 ≤ y ≤ pi/2. Resuelve este problema usando el Primer Principal.
Solución:
En primer lugar, tomando sen en ambos lados, por lo tanto, obtenemos x = sen y esta ecuación no es más que una función de y. En lugar de encontrar dy/dx, encontraremos dx/dy, por lo que, por definición de derivada, podemos escribir ((f(y + h) – f(y))/h), donde h -> 0 bajo la condición límite (ver cuarta línea). Ahora reemplace la función con ((sin(y + h) – siny)/h) donde h -> 0 bajo la condición límite. Usando la identidad podemos resolver más. Como vemos en la última línea de la siguiente solución, siny y cosy no dependen del límite h -> 0, por eso los eliminamos.
sen(sen x) = sen y
x = sen y
Por definición de derivada,
dx/dy = lím h->0 {f(y + h) – f(y)} / h
= lim h->0 { sin(y + h) – siny } / h
Usando identidad: sin(A + B) = sinA.cosB + cosA.sinB , podemos escribir,
= lím h->0 (sen y . cos h + cos y . sen h – sen y) / h
= lím h->0 (sen y . cos h – sen y + cos y . sen h) / h
= lim h->0 {sen y(cos h – 1) / h} + {cos y . pecado h) / h}
= sen y. lím h->0 {(cos h – 1) / h} + cos y. lím h->0 {sin h / h}
Ahora, habíamos tomado -1 común de la expresión (cos h-1) y obtenemos (ver en la primera línea de la figura a continuación). Ahora, usando la fórmula escrita en la línea 2 de la figura a continuación, podemos escribir nuestra expresión dx/dy = cos y, si recíprocamos este término obtenemos dy/dx = 1/cos y esto. Sabemos que sen 2 x + cos 2 x = 1, al simplificar esta fórmula para obtener nuestra respuesta, la simplificamos hasta la sexta línea de la siguiente figura.
Pero, ¿cómo habíamos escrito la respuesta final a este problema?
Dado que -pi/2 ≤ sen -1 x ≤ pi/2. Por lo tanto, -pi/2 ≤ y ≤ pi/2, habíamos escrito y en lugar de sen -1 x, mira la segunda línea de la figura anterior, habíamos escrito x = sen, si escribimos esto para y podemos escribir esto como y = sin -1 x esto, por eso habíamos escrito y en lugar de sin -1 x. Esto implica 0 ≤ cosy ≤ 1 porque y es un ángulo que se encuentra solo en el primer y cuarto cuadrante, pero una cosa a tener en cuenta aquí, ya que cosy está en el denominador de dy/dx, por lo que no puede ser cero,
Ahora eliminamos la igualdad 0 < cos y ≤ 1 por esta desigualdad, podemos decir claramente que acogedor es una propiedad positiva, por lo tanto, podemos eliminar el signo -ve de la penúltima línea de la figura a continuación. Entonces, esto implica dy/dx = 1 sobre la cantidad raíz cuadrada de (1 – x 2 ), que es nuestra respuesta requerida.
Nota: en la solución, después de eliminar el cuadrado, obtenemos la raíz cuadrada en otro lado y con la raíz cuadrada +ve y -ve, ambos signos tienen lugar, lo que se denota con +-squareroot en la solución.
= sen y. lim h->0 { (cos h – 1) / h } + cos y. lím h->0 { sin h / h }
Usando la fórmula: lim h->0 (1 – cos h) / h = 0 y lim h->0 sen h / h = 1 , podemos escribir,
dx / dy = cos y
dy / dx = 1 / cos y …..(1)
Sabemos que sen 2 y + cos 2 y = 1, entonces cos 2 y = 1 – sen 2 y
⇒ cos = +- √(1 – sen 2 y), tomando sen = x
obtenemos, acogedor = +-√(1 – x 2 )
dy / dx = 1 / √(1 – x 2 )
Si dibujamos la gráfica del seno inverso x, entonces la gráfica se ve así:

Ejemplos
Ejemplo 1: Derive la función f (x) = cos -1 x usando el primer principio.
Solución:
Para resolver y encontrar el cos -1 x, debemos recordar a continuación tres fórmulas enumeradas.
- lím h->0 {f(x + h) – f(x)} / h
- cos -1 x + sen -1 x = pi/2
- cos -1 x = pi/2 – sen -1 x
Ahora, vamos a resolver, tenemos.
f (x) = cos -1 x
f (x + h) = cos -1 (x + h)
lím h->0 {cos -1 (x + h ) – cos -1 (x)} / h
lím h->0 {pi/2 – sen -1 (x + h) – (pi/2 – sen -1 x) } / h
lím h->0 {pi/2 – sin -1 (x + h) – pi/2 + sin -1 x } / h
Tomando – signo común, obtenemos
– lím h->0 {sin -1 (x + h) – sin -1 x} / h
Como sabemos que lim h->0 { sin -1 (x + h) – sin -1 x } / h = 1 / √(1 – x 2 )
Poniendo el valor en nuestra solución obtenemos,
– 1 / √(1 – x 2 )
Si dibujamos la gráfica de cos inversa x, entonces la gráfica se ve así.

Ejemplo 2: Resolver f(x) = tan -1 (x) usando el primer principio.
Solución:
Para resolver y encontrar tan -1 x, debemos recordar algunas fórmulas, que se enumeran a continuación.
- lím h->0 {f(x + h) – f(x)} / h
- bronceado -1 (θ/θ) = 1
- bronceado -1 x – bronceado -1 y = bronceado -1 [(x – y) / (1 + xy)]
f(x) = bronceado -1 x
f(x + h) = bronceado -1 (x + h)
Aplicar 1ra fórmula
lím h->0 {tan -1 (x + h) – tan -1 x } / h
Ahora aplique la tercera fórmula
lím h->0 tan -1 [(x – h – x) / (1 + (x + h)x] / h
lim h->0 tan -1 [(h / (1 + x 2 + xh ] / h . [(1 + x 2 + xh) / (1 + x 2 + xh)]
lim h->0 tan -1 {h / 1 + x 2 + xh} / {h / 1 + x 2 + xh} . lím h->0 1 / 1 + x 2 + xh
Ahora hicimos la solución como para que apliquemos la segunda fórmula.
= 1 . 1 / (1 + x 2 + x . 0)
= 1 / (1 + x2 )
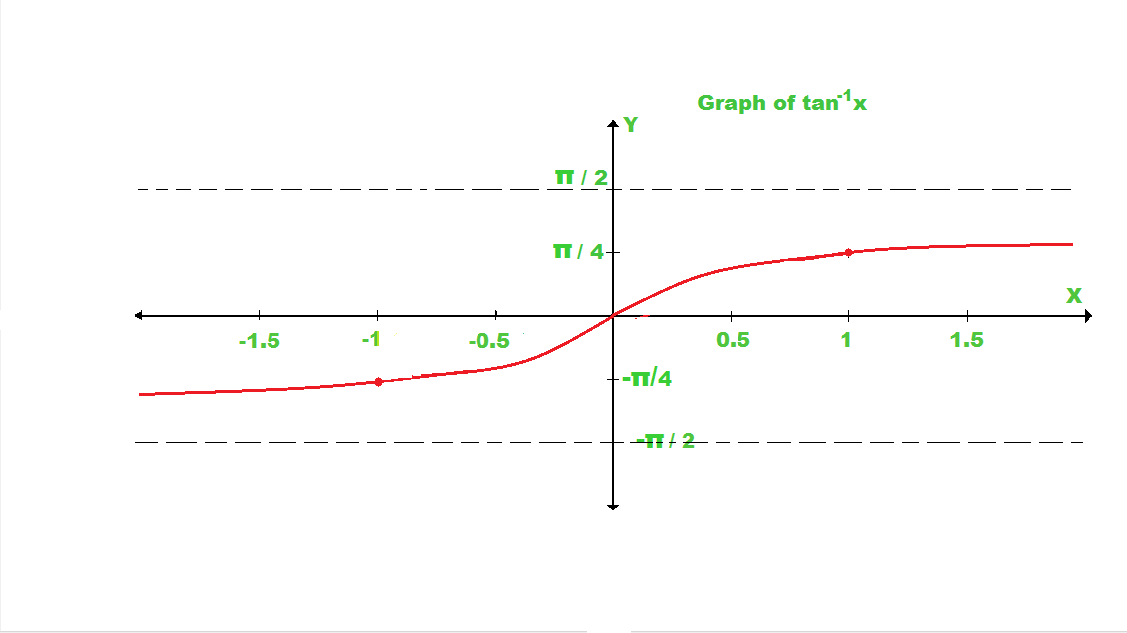
Si dibujamos la gráfica de tan inversa x, entonces la gráfica se ve así.
La derivada de funciones trigonométricas inversas usando la regla de la string
Antes de usar la regla de la string, primero debemos saber qué es la regla de la string.
La expresión anterior demostró la regla de la string, donde u es la primera función y v es la segunda función y para aplicar la regla de la string primero tenemos que tomar la derivada de u y multiplicar con v en el otro segmento, tenemos que tomar la derivada de v y lo multiplicamos por u y luego sumamos ambos. Usamos esta regla de la string para encontrar la derivada de la función trigonométrica inversa.
Fórmulas de funciones trigonométricas inversas
En la siguiente figura hay una lista de fórmulas de funciones trigonométricas inversas que usaremos para resolver los problemas al resolver la derivada de funciones trigonométricas inversas.

Ejemplos
Tomemos algunos de los problemas basados en la regla de la string para entender correctamente este concepto.
Nota: En todas las soluciones a continuación y’ significa dy/dx
Problema 1: y = tan -1 (1/x)
Solución :
Tenemos que encontrar la derivada de la pregunta anterior, así que primero, tenemos que sustituir las fórmulas de tan -1 x como discutimos en la lista anterior (línea 3). Entonces, tenemos que aplicar la regla de la string. Luego ponga el valor de x en esas fórmulas que son (1/x) luego, al aplicar la regla de la string, hemos resuelto la pregunta tomando sus derivados.
Usando la regla de la string,
y’ = (tan- 1x )’
= {1/1 + (1/x 2 ) } . (-1/ x2 )
= – x 2 / (x 2 + 1) . x2 _
Problema 2: y = sen -1 (1 – x)
Solución:
Tenemos que encontrar la derivada de la pregunta anterior, así que primero, tenemos que sustituir las fórmulas de tan -1 x como discutimos en la lista anterior (línea 1). Entonces, tenemos que aplicar la regla de la string. Luego ponga el valor de x en esas fórmulas que son (1 – x) luego, aplicando la regla de la string, hemos resuelto la pregunta tomando sus derivados.
Usando la regla de la string,
y’ = (sen -1 (1 – x))’
= 1 / 1 – (x – 1) 2
= 1 / √(1 – (x 2 – 2x + 1))
= 1 / √(2x – x2 )
Problema 3: y = (1/a) tan -1 (x/a)
Solución:
Como ya habíamos resuelto el primer problema de la misma manera, vamos a resolver este problema también, tenemos que encontrar la derivada de la pregunta anterior, así que primero, tenemos que sustituir las fórmulas de tan -1 x como discutimos en la lista anterior (línea 3). Luego aplica la regla de la string. Como vemos 1/a es constante, por lo que lo sacamos y aplicamos la regla de la string en tan -1 (x/a). Lo resolvió tomando la derivada después de aplicar la regla de la string.
Usando la regla de la string,
y’ = ((1/a) tan -1 (x/a))’
= (1/a) {1/(1 + (x/a))} . (x/a)’
= 1 / un . {1 / (1+ (x 2 / a 2 ))} . (1/a)
= 1 / un 2 . {un / (un 2 + x2)}
= un / un 2 + x 2
Problema 4: y = cot -1 (1/x 2 )
Solución:
Como estamos resolviendo los tres problemas anteriores de la misma manera, este problema resolverá
Usando la regla de la string,
y’ = (cot -1 (1 / x 2 ))’
= { – 1 / (1 + (1 / x 2 )) 2 } . (1 / x 2 )’
= { – 1 / (1 + (1 / x 4 )) . (-2x -3 )
= 2x 4 / (x 4 + 1)x 3
= 2x / (1 + x4 )
Tenemos que encontrar la derivada de cot -1 (1/x 2 ), así que como estamos siguiendo primero tenemos que sustituir las fórmulas de cot -1 x en la lista anterior de fórmulas trigonométricas (línea 4). Luego aplique la regla de la string y encuentre la derivada del problema y después de resolver, obtengamos la respuesta requerida.
La derivada de la función trigonométrica inversa como función implícita
En primer lugar tenemos que saber acerca de la función implícita. ¿Qué son las funciones implícitas? Tomemos una función por ejemplo, y = 2x + 3. Entonces, en esta función, la variable y depende de la variable x, lo que significa que cuando el valor de x cambie en el valor de la función, también cambiará. Entonces, este tipo de función en la que la variable dependiente (y) está aislada significa que viene sola en un lado (lado izquierdo), estas funciones no son funciones implícitas, son funciones explícitas.
Tomemos otro ejemplo, x + sen xy -y = 0. Como vemos en esta función, no podemos separar ninguna variable por sí sola en un lado, lo que significa que no podemos aislar ninguna variable, porque tenemos ambas variables x e y como el ángulo del pecado. Entonces, este tipo de función en la que no podemos aislar la variable. Este tipo de función se conoce como funciones implícitas. Tomemos el problema y lo resolvemos usando la diferenciación implícita.
Ejemplo: y = cos -1 x
Solución:
Para encontrar la derivada de la función trigonométrica inversa usando diferenciación implícita. Para empezar a resolver primero tenemos que sacar la derivada x en ambos lados, la derivada de cos(y) frente a x es -sin(y)y’. El recíproco de sin es cosec por lo que podemos escribir en lugar de -1/sin(y) es -cosec(y) (ver en la línea 7 en la figura de abajo). Ahora tenemos que escribir la respuesta en términos de x, de la ecuación (1) dibujamos el triángulo para cos(y) = x y encontramos la perpendicular del triángulo. Ahora la fórmula de cosec es hip/perpendicular, ahora con la ayuda del triángulo que habíamos dibujado, podemos encontrar el cosec(y) poniéndolo en la fórmula. Luego pon el valor de cosec(y) en la ecuación(2). Obtenemos nuestra respuesta requerida (ver la última línea).
y = cos -1 x
y’ = (cos x)’
podemos escribir,
porque y = x …(1)
d/dx (cos y) = d/dx (x)
(-sen y) y’ = 1 / sen
y’ = -coseg y …(2)
de la ecuación (1), fórmula de cos(x) = base / hyp , podemos encontrar la perpendicular del triángulo
perpendiculares = √(1 – x 2 )
fórmula de cosec(x) = hyp / perpendicular, que es,
= 1 / √(1 – x2 )
Poniendo el valor de cosec en la ecuación (2), obtenemos
y’ = -1 / √(1 – x 2 )
Publicación traducida automáticamente
Artículo escrito por srishivansh5404 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
