En este artículo, cubriremos las pruebas de la derivada de las funciones ln(x) y e x . Antes de continuar, hay dos cosas que debemos revisar:
El primer principio de la derivada
Encontrar la derivada de una función calculando este límite se conoce como diferenciación a partir de primeros principios. La derivada por el primer principio se refiere al uso del álgebra para encontrar una expresión general para la pendiente de una curva. También se conoce como el método delta . La derivada es una medida de la tasa de cambio instantánea, que es igual a
e en términos de límite
El número e, conocido como número de Euler , es una constante matemática aproximadamente igual a 2,71828 . El descubrimiento de la constante en sí se atribuye a Jacob Bernoulli en 1683, quien intentó encontrar el valor de la siguiente expresión (que es igual a e).
Prueba de la derivada de e x
Ejemplo 1: Encuentra la derivada de 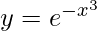 ?
?
Solución:
Por la regla de la string,
Ejemplo 2: Encuentra la derivada de 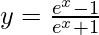 ?
?
Solución:
Use aquí la regla del cociente:
Prueba de la derivada de ln(x)
Ejemplo 1: ¿Encuentra la derivada de 3ln(x)?
Solución:
3ln(x)’ = 3(1/x) = 3/x
Ejemplo 2: ¿Encuentra la derivada de ln(x)/5?
Solución:
(ln(x)/5)’ = 1/5(ln(x))′ = (1/5) (1/x) = 1/5x
Publicación traducida automáticamente
Artículo escrito por rathoreatul27 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA



