Prerrequisito: Conjunto 2 de predicados y cuantificadores , equivalencias proposicionales Cada teorema en matemáticas, o cualquier tema, está respaldado por pruebas subyacentes. Estas pruebas no son más que un conjunto de argumentos que son evidencia concluyente de la validez de la teoría. Los argumentos se enstringn usando Reglas de Inferencias para deducir nuevas declaraciones y, en última instancia, probar que el teorema es válido.
Definiciones importantes:
1. Argumento: una secuencia de declaraciones, premisas , que terminan con una conclusión.
2. Validez: se dice que un argumento deductivo es válido si y solo si toma una forma que hace imposible que las premisas sean verdaderas y, sin embargo, la conclusión sea falsa.
3. Falacia: un razonamiento incorrecto o un error que conduce a argumentos inválidos.
Estructura de un argumento: como se define, un argumento es una secuencia de declaraciones llamadas premisas que terminan con una conclusión.
Premises -Conclusion -
![]() is a tautology, then the argument is termed valid otherwise termed as invalid. The argument is written as –
is a tautology, then the argument is termed valid otherwise termed as invalid. The argument is written as –
Reglas de inferencia: los argumentos simples se pueden usar como bloques de construcción para construir argumentos válidos más complicados. Ciertos argumentos simples que se han establecido como válidos son muy importantes en términos de su uso. Estos argumentos se denominan reglas de inferencia. Las reglas de inferencia más utilizadas se tabulan a continuación:
De manera similar, tenemos reglas de inferencia para declaraciones cuantificadas:
Veamos cómo se pueden usar las reglas de inferencia para deducir conclusiones a partir de argumentos dados o verificar la validez de un argumento dado. Ejemplo: Demuestre que las hipótesis “No hace sol esta tarde y hace más frío que ayer”, “Iremos a nadar solo si hace sol”, “Si no vamos a nadar, entonces haremos un viaje en canoa”, y “Si hacemos un viaje en canoa, estaremos en casa al atardecer” llevan a la conclusión “Estaremos en casa al atardecer”. El primer paso es identificar proposiciones y usar variables proposicionales para representarlas. ![]() “Hace sol esta tarde”
“Hace sol esta tarde” ![]() “Hace más frío que ayer”
“Hace más frío que ayer” ![]() “Iremos a nadar”
“Iremos a nadar” ![]() “Haremos un viaje en canoa”
“Haremos un viaje en canoa” ![]() “Estaremos en casa al atardecer” Las hipótesis son –
“Estaremos en casa al atardecer” Las hipótesis son – ![]() ,
, ![]() ,
, ![]() y
y ![]() . La conclusión es:
. La conclusión es: ![]() para deducir la conclusión, debemos usar las reglas de inferencia para construir una prueba usando las hipótesis dadas.
para deducir la conclusión, debemos usar las reglas de inferencia para construir una prueba usando las hipótesis dadas. 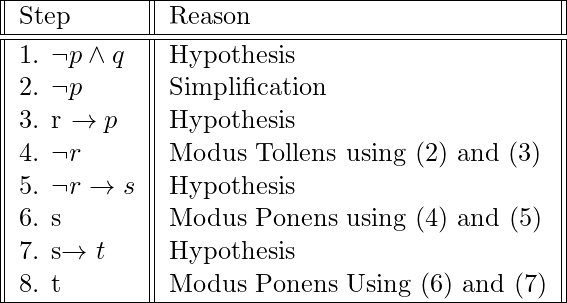 Principio de Resolución: Para entender el principio de Resolución, primero necesitamos conocer ciertas definiciones.
Principio de Resolución: Para entender el principio de Resolución, primero necesitamos conocer ciertas definiciones.
- Literal: una variable o negación de una variable. P.ej-
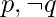
- Suma – Disyunción de literales. P.ej-
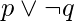
- Producto – Conjunción de literales. P.ej-
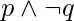
- Cláusula: una disyunción de literales, es decir, es una suma.
- Resolvente: para dos cláusulas cualquiera
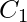 y
y 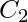 , si hay un literal
, si hay un literal 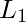 en
en 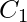 que es complementario a un literal
que es complementario a un literal 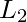 en
en 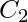 , entonces eliminar ambos y unir las cláusulas restantes a través de una disyunción produce otra cláusula
, entonces eliminar ambos y unir las cláusulas restantes a través de una disyunción produce otra cláusula  .
.  se llama el resolutivo de
se llama el resolutivo de 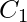 y
y 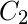
Por ejemplo,
[Tex]C_{2} = \neg p\vee \neg s \vee t[/Tex]
Aquí, ![]() y
y ![]() son complementarios entre sí. Eliminarlas y unir las cláusulas restantes con una disyunción
son complementarios entre sí. Eliminarlas y unir las cláusulas restantes con una disyunción ![]() nos da: Podríamos omitir la parte de eliminación y simplemente unir las cláusulas para obtener el mismo resolutivo.
nos da: Podríamos omitir la parte de eliminación y simplemente unir las cláusulas para obtener el mismo resolutivo. ![]() Esta es también la Regla de Inferencia conocida como Resolución. Teorema – Si
Esta es también la Regla de Inferencia conocida como Resolución. Teorema – Si ![]() es el resolvente de
es el resolvente de ![]() y
y ![]() , entonces
, entonces ![]() también es la consecuencia lógica de
también es la consecuencia lógica de ![]() y
y ![]() . El principio de resolución: dado un conjunto
. El principio de resolución: dado un conjunto ![]() de cláusulas, una deducción (resolución) de
de cláusulas, una deducción (resolución) de ![]() from
from ![]() es una secuencia finita
es una secuencia finita ![]() de cláusulas, de modo que cada una
de cláusulas, de modo que cada una ![]() es una cláusula en
es una cláusula en ![]() o un resolutor de cláusulas que preceden
o un resolutor de cláusulas que preceden ![]() y
y ![]() . Podemos utilizar el principio de resolución para comprobar la validez de los argumentos o deducir conclusiones de ellos. Otras Reglas de Inferencia tienen el mismo propósito, pero la Resolución es única. Es completo por sí mismo. No necesitaría ninguna otra regla de inferencia para deducir la conclusión del argumento dado. Para hacerlo, primero necesitamos convertir todas las premisas a la forma de cláusula. El siguiente paso es aplicarles la regla de inferencia de resolución paso a paso hasta que ya no se pueda aplicar más. Por ejemplo, considere que tenemos las siguientes premisas:
. Podemos utilizar el principio de resolución para comprobar la validez de los argumentos o deducir conclusiones de ellos. Otras Reglas de Inferencia tienen el mismo propósito, pero la Resolución es única. Es completo por sí mismo. No necesitaría ninguna otra regla de inferencia para deducir la conclusión del argumento dado. Para hacerlo, primero necesitamos convertir todas las premisas a la forma de cláusula. El siguiente paso es aplicarles la regla de inferencia de resolución paso a paso hasta que ya no se pueda aplicar más. Por ejemplo, considere que tenemos las siguientes premisas:
[Tex]s\rightarrow \neg r[/Tex]
El primer paso es convertirlos a forma de cláusula:
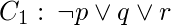
[Tex]C_{3}: \:p[/Tex]
From the resolution of
and
,
From the resolution of
and
,
From the resolution of
and
,
Therefore, the conclusion is
.
Nota: Las implicaciones también se pueden visualizar en el octágono como 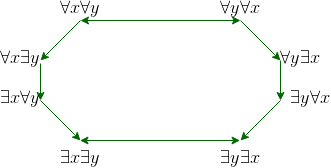 muestra cómo cambia la implicación al cambiar el orden de que existe y para todos los símbolos. Preguntas de GATE CS Corner Practicar las siguientes preguntas lo ayudará a evaluar su conocimiento. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques. 1. GATE CS 2004, Pregunta 70 2. GATE CS 2015 Conjunto-2, Pregunta 13 Referencias – Reglas de inferencia – Universidad Simon Fraser Reglas de inferencia – Falacia de Wikipedia – Libro de Wikipedia – Matemáticas discretas y sus aplicaciones por Kenneth Rosen Este artículo es una contribución por Chirag Manwani. Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
muestra cómo cambia la implicación al cambiar el orden de que existe y para todos los símbolos. Preguntas de GATE CS Corner Practicar las siguientes preguntas lo ayudará a evaluar su conocimiento. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques. 1. GATE CS 2004, Pregunta 70 2. GATE CS 2015 Conjunto-2, Pregunta 13 Referencias – Reglas de inferencia – Universidad Simon Fraser Reglas de inferencia – Falacia de Wikipedia – Libro de Wikipedia – Matemáticas discretas y sus aplicaciones por Kenneth Rosen Este artículo es una contribución por Chirag Manwani. Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

![Rendered by QuickLaTeX.com \begin{tabular}{||c||c||c||} \hline Rule of Inference & Tautology & Name\\ \hline \rule{0pt}{8ex} \shortstack[l]{p \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore q}& (p\wedge (p\rightarrow q)) \rightarrow q & Modus Ponens \\ \hline \rule{0pt}{8ex} \shortstack[l]{\neg q \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore \neg p}& (\neg q \wedge (p\rightarrow q)) \rightarrow \neg p & Modus Tollens \\ \hline \rule{0pt}{8ex} \shortstack[l]{p\rightarrow q \\ q\rightarrow r \\ \rule{1.3cm}{0.5pt}\\ \therefore p \rightarrow r}& ((p\rightarrow q) \wedge (q\rightarrow r)) \rightarrow (p\rightarrow r) & Hypothetical syllogism \\ \hline \rule{0pt}{8ex} \shortstack[l]{ \neg p \\ p\vee q \\ \rule{0.8cm}{0.5pt}\\ \therefore q} & (\neg p \wedge (p\vee q)) \rightarrow q & Disjunctive Syllogism \\ \hline \rule{0pt}{8ex} \shortstack[l]{p \\ \rule{1.5cm}{0.5pt} \\ \therefore (p \vee q)}& p\rightarrow (p\vee q) & Addition \\ \hline \rule{0pt}{8ex} \shortstack[l]{ (p\wedge q)\rightarrow r \\ \rule{2.3cm}{0.5pt}\\ \therefore p\rightarrow (q\rightarrow r)} & ((p\wedge q)\rightarrow r) \rightarrow (p\rightarrow (q\rightarrow r)) & Exportation\\ \hline \rule{0pt}{8ex} \shortstack[l]{p\vee q\\\neg p\vee r \\ \rule{1.2cm}{0.5pt} \\ \therefore q\vee r}& ((p\vee q) \wedge(\neg p\vee r)) \rightarrow q\vee r & Resolution \\ \hline \end{tabular}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d19335616a8b6adc2da3e88c1219443c_l3.png)
![Rendered by QuickLaTeX.com \begin{tabular}{||l||l||} \hline Rule of Inference & Name\\ \hline \hline \rule{0pt}{6ex} \shortstack[l]{\forall xP(x) \\ \rule{1cm}{0.5pt}\\ \therefore P(c)} & Universal instantiation \\ \hline \rule{0pt}{6ex} \shortstack[l]{P(c) for an arbitrary c\\ \rule{4cm}{0.5pt}\\ \therefore \forall xP(x)} & Universal generalization \\ \hline \rule{0pt}{6ex} \shortstack[l]{\exists xP(x)\\ \rule{3cm}{0.5pt} \\ \therefore P(c)\:for\:some\:c} & Existential instantiation \\ \hline \rule{0pt}{6ex} \shortstack[l]{P(c) for some c \\ \rule{2.6cm}{0.5pt}\\ \therefore \exists xP(x)} & Existential generalization \\ \hline \end{tabular}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-59b657d84c2d674466fcdfaec09d9c88_l3.png)