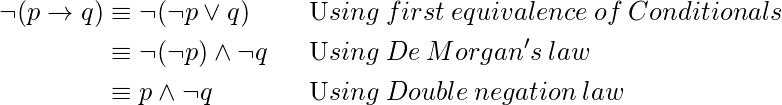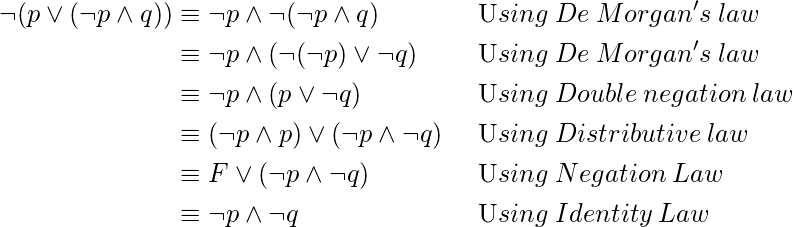Matemáticas | Equivalencias Proposicionales

Introducción
Se dice que dos expresiones lógicas son equivalentes si tienen el mismo valor de verdad en todos los casos. A veces, este hecho ayuda a probar un resultado matemático al reemplazar una expresión con otra expresión equivalente, sin cambiar el valor de verdad de la proposición compuesta original.

Tipos de proposiciones basadas en valores de verdad

Hay tres tipos de proposiciones cuando se clasifican de acuerdo con sus valores de verdad
1. Tautología: una proposición que siempre es verdadera se llama tautología.
2. Contradicción: una proposición que siempre es falsa se llama contradicción.
3. Contingencia: una proposición que no es ni una tautología ni una contradicción se llama contingencia.

Ejemplo,

1.  is a tautology.
2.  is a contradiction.
3.  is a contingency.

Definición de equivalencia lógica
Formalmente, se dice que
dos proposiciones y son lógicamente equivalentes si es una tautología . La notación se utiliza para denotar que y son lógicamente equivalentes.
Una forma de probar que dos proposiciones son lógicamente equivalentes es usar una tabla de verdad. La tabla de verdad debe ser idéntica para que todas las combinaciones de las proposiciones dadas sean equivalentes. Pero este método no siempre es factible ya que las proposiciones pueden ser cada vez más complejas tanto en el número de variables proposicionales utilizadas como en el tamaño de la expresión.
En este caso, debe haber una mejor manera de demostrar que las dos proposiciones dadas son lógicamente equivalentes. Esa mejor manera es construir una prueba matemática que use equivalencias lógicas ya establecidas para construir equivalencias lógicas adicionales más útiles.
Algunas equivalencias lógicas básicas establecidas se tabulan a continuación:

Las Equivalencias Lógicas anteriores usan solo conjunción, disyunción y negación. Otras equivalencias lógicas que usan condicionales y bicondicionales son:

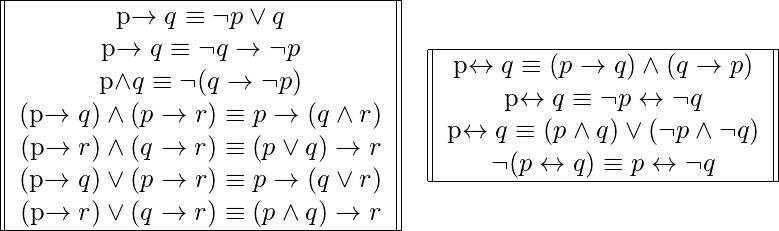
Ejemplo,
Demuestra que .

Considering LHS,

Otro ejemplo,
Mostrar que .

Considering LHS,

Los ejemplos anteriores podrían resolverse fácilmente usando una tabla de verdad. Pero esto solo se puede hacer para una proposición que tenga un pequeño número de variables proposicionales. Cuando el número de variables crece, el método de la tabla de verdad se vuelve poco práctico.
Para una proposición que tiene 20 variables, las filas deben evaluarse en la tabla de verdad. Esto puede ser fácil de hacer con una computadora, pero incluso una computadora fallaría al calcular la tabla de verdad de una proposición que tiene 1000 variables.

Preguntas de GATE CS Corner

Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
1. GATE CS 2008, Pregunta 33
2. GATE CS 2014 Conjunto-2, Pregunta 63
3. GATE CS 2006, Pregunta 27
4. GATE CS 2015 Conjunto-3, Pregunta 65

Referencias,
equivalencia lógica – Wikipedia
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen

Este artículo es una contribución de Chirag Manwani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.