División de Expresiones Algebraicas

Una expresión algebraica se puede escribir como el producto de sus factores. Considere una expresión, 7yz +3y. Vemos que 7yz se puede escribir como 7 × y × z. Los factores 7, y y z no pueden expresarse más como producto de factores. Entonces, podemos concluir que 7 × y × z es una forma irreducible de 7yz.

Expresar la expresión algebraica como un producto de sus factores se llama factorización. Los factores se pueden representar en forma de números, variables o expresiones algebraicas. 

Técnicas de Factorización 

Entendamos cuatro formas de factorización.   

Técnica de Factores Comunes

En este método, cada término se escribe como un producto de factores irreducibles. Luego se identifican los factores comunes y se expresan usando la ley distributiva.

Ejemplo: factorizar 18y ² z +21 yz ²

Solución:

18y ² z = 2 × 3 × 3 × y × y × z

21yz ² = 3 × 7 × y × z × z

Factores comunes : 3, y, z

Asi que, 

18y ² z +21 zy ² = (2 × 3 × 3 × y × y × z) + (3 × 7 × y × z × z)

                       = 3 × y × z (6 × y + 7 × z)

                       = 3 yz(6y + 7z)

Técnica de reagrupación de términos

Muchas veces no existe un factor común a todos los términos de la expresión. En tal situación, los términos se reagrupan hasta que los factores alcanzan el estado de irreductibilidad.

Ejemplo: Factorizar 16mn – 12m +12n – 9

Solución:

Es claro que en esta expresión no hay factores comunes entre todos los términos. Necesitamos reagrupar los términos.

16mn-12m = 4m(4n-3)

12n-9 = 3 (4n-3)

Entonces, 16mn – 12m +12n -9 = 4m(4n-3)+3 (4n-3)

              Podemos tomar 4n-3 común entre estos términos

                        = (4n-3) (4m+3)

Técnica de uso de identidades

Podemos hacer uso de identidades para la factorización.

(a + b) ² = a ² + 2ab +b ² ——–(I)

(ab) ² = a ² + b ² – 2ab ———-(II)

(a + b) (a- b)= a ² -b ² ———–(III)

Ejemplo 1: factoriza 25 x ² – 49

Solución:

25 x ² – 49 = (5x) ² – (7) ²

Usando (III), podemos reescribirlo como

 = (5x+7)(5x-7)

Ejemplo 2. Factorizar m ² + 36 + 12m

Solución: 

m ² + 36 + 12m 

= metro ² + 2(6)(metro)+6 ²

Usando (I) se puede escribir como

= (m+6) ² 

Técnica para usar la forma (x +a) (x +b) como x ² + (a + b)x + ab

Sabemos que x ² + (a + b)x +ab = (x +a)(x+ b)

Ejemplo: factorizar m ² +3m+2

Aquí, necesitamos encontrar los factores tales que su suma sea 3 mientras que su producto sea 2.

Estos son 2,1

Entonces, m ² + 3 m + 2 = m ² + 2 m + m + 2

                       = m(m+2) + 1(m+2)

                       = (m+1)(m+2)

División de Expresiones Algebraicas 

La división es el inverso de la multiplicación. Antes de discutir la división, recapitulemos algunos términos asociados con los polinomios. Dependiendo del número de términos en una expresión, decidimos si es monomio, binomio o polinomio. 

Monomio contiene un término, mientras que un binomio contiene dos términos. En términos generales, un polinomio contiene uno o más términos con un coeficiente distinto de cero.

Ejemplo de monomio: 4xy, 89z, 56pqr, -9

Ejemplo de binomio: 34x+45y, 9xz+5xy

Ejemplo de polinomio: w+ x +y +z, 3r+5t-8z-7p

Consideremos los siguientes casos de división:

División de monomio por un monomio

Este es el caso más simple donde tanto el dividendo como el divisor son monomios. Estos se factorizan y los factores comunes se cancelan.

Ejemplo 1: Divide 24y ³ entre 8y

Solución:

24y ³ se puede escribir como 2* 2 * 2 * 3* y * y * y 

8y se puede escribir como 2*2*2*y.

Entonces, necesitamos evaluar (2* 2 * 2 * 3* y * y * y)/(2*2*2*y)

Cancelando los factores comunes,  

Obtenemos el resultado como 3 y ² .

Cheque: 3y ² x 8y =24y ³

Ejemplo 2. Divide 20mnz por 4 m

Solución:

Dividendo = 4 * 5 * m * n * z

divisor = 4 * m

Dividiendo obtenemos, (4* 5* m*n*z)/(4 *m)= 5 nz

Comprobar: 4m* 5nz = 20mn

División de polinomio por un monomio

Ejemplo 1: Divide 32(m ² np+ mn ² p+mnp ² ) por 4mnp

Solución:

Dividendo= 32(m ² np+ mn ² p+mnp ² ) = 4 * 8 *mnp (m +n+ p)

Divisor= 4mnp

Al dividir, (4 * 8 *mnp (m +n+ p)/(4mnp)

= 8(m+n+p)

Ejemplo 2: Divide 36pqr + 12r por 4r 

Solución:

Dividendo =36pqr+ 12r =12 r(3pq+1)

divisor= 4r

Entonces, (36pqr+ 12r ) / 4r se puede escribir como

= 12 r (3pq+1) /4r 

= 4r *3 *(3pq+1)/4r

Cancelando los términos comunes,

Obtenemos, 3(3pq+1)

División de polinomio por un polinomio

A veces hay algunos factores comunes entre el dividendo y el divisor. La estrategia aquí también es cancelar los factores comunes para obtener el cociente.

Ejemplo 1: (12m ² + 24m)/(m+2)

12m ² +24 m se puede escribir como 12m(m+2)

Entonces, (12m ² + 24 m)/(m+2) =12m(m+2)/(m+2)= 12m

entonces el cociente es 12m

Comprobar: 12m × (m+2)= 12m ² +24m

Podemos aplicar el método de división larga también para calcular el cociente y el resto. Los términos del dividendo se dividen repetidamente por el primer término del divisor.

Ejemplo 2: Dividir m ⁴ -m ³ +m ² +5 entre m+1

Solución:

Este dividendo se puede reescribir como  

m3 (m ^{+ 1} )-2m2 (m+1)+3m(m+1)-3(m+1)+8

= m+1(m ³ -2m ² +3m-3)+8

La división por m+1 da

Cociente =(m ³ -2m ² +3m-3)

Resto=8

Ejemplo 3: Dividir m ⁴ – n ⁴ por m ² – n ²

Solución:

Usando la identidad a ² -b ² = (ab) (a + b)

Podemos escribir m ⁴ – n ⁴ como (m ² – n ² )(m ² + n ² )

Entonces, cancelando los términos comunes en dividendo y divisor, obtenemos el cociente como m ² +n ²

Error 

Generalmente, un error es un error o una diferencia en el valor calculado debido a la inexactitud del número calculado con respecto a su valor real.

Puntos a recordar para evitar errores:

• El coeficiente 1 generalmente no se escribe. Al agregar términos similares, no olvide incluirlo en la suma.

por ejemplo, la suma de 4x y x+4 es (4x+x+4), es decir, 5x+4 no sólo 4x+4.

• Al sustituir valores negativos, utilice corchetes.

por ejemplo, el producto de 5 y (2x+3), es decir, 5(2x+3) es igual a 10x+15, no sólo a 10x+9.

• Cuando una expresión escrita entre paréntesis se multiplica por una constante fuera del paréntesis, abra los paréntesis con cuidado. Asegúrate de que cada término de la expresión se tenga que multiplicar por la constante.

Por ejemplo, si se da que x=-2, entonces 5x-2 se puede escribir como 5(-2)-2, que es igual a -12.

• Al elevar al cuadrado cualquier monomio, tanto el coeficiente de contacto como la variable se elevan al cuadrado.

por ejemplo, el cuadrado de 2x, es decir, (2x) ² es igual a 4x ² .

• Cuando eleves un binomio al cuadrado, siempre usa las fórmulas correctas.

por ejemplo, el cuadrado de (2x+3), es decir, (2x+3) ² es igual a 4x ² +9+12x.

• Cuando un polinomio se divide por un monomio, cada término del numerador del polinomio se divide por el monomio presente en el denominador.

 

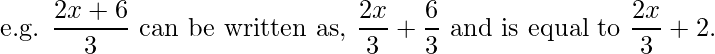
Conclusión:

Este artículo enseña claramente varios métodos para hacer la factorización. Además, analiza la división de expresiones algebraicas con ejemplos propios.

• Cuando un monomio se divide por otros monomios, el coeficiente del cociente de dos monomios es igual al cociente de sus coeficientes.
• Cuando un monomio se divide por otros monomios, la variable del cociente de dos monomios es igual al cociente de las variables de monomios.
• Podemos comprobar el resultado por Dividendo = Resto + Divisor * Cociente