Gráficas de Funciones Trigonométricas Inversas – Trigonometría

Las funciones trigonométricas inversas son las funciones inversas de las razones trigonométricas, es decir, sin, cos, tan, cot, sec, cosec. Estas funciones se utilizan ampliamente en campos como la física, las matemáticas, la ingeniería y otros campos de investigación. Hay dos notaciones populares utilizadas para funciones trigonométricas inversas:

Agregar «arco» como prefijo.

Ejemplo: arcsen(x), arccos(x), arctan(x), …

Agregar «-1» como superíndice.

Ejemplo: sen ^-1 (x), cos ^-1 (x), tan ^-1 (x), …

En este artículo, aprenderemos sobre los gráficos y la naturaleza de varias funciones inversas.

Función inversa de seno, y = sen ^-1 (x)

sin ^-1 (x) es la función inversa de sin(x). Su dominio es [−1, 1] y su rango es [- π/2, π/2]. Se cruza con el eje de coordenadas en (0,0). Es una función impar y es estrictamente creciente en (-1, 1).

Gráfica de función

Análisis de funciones

y ∈ \big[\frac{−\pi}{2}, \frac{\pi}{2}\big]

Dominio	$x ∈ [−1, 1]$
Rango	$y ∈ \big[\frac{−\pi}{2}, \frac{\pi}{2}\big]$
X-intersección	$x = 0$
Y – Intercepción	$y = 0$
Mínimos	$\big(−1, \frac{−\pi}{2}\big)$
Máxima	$\big(1, \frac{\pi}{2}\big)$
Puntos de inflexión	$(0, 0)$
Paridad	Función impar
monotonicidad	En (-1, 1) estrictamente creciente

Problemas de muestra sobre la función del seno inverso

Problema 1: Encuentra el valor principal de la ecuación dada:

y = sen ^-1 (1/√2)

Solución:

Se nos da que:

y = sen ^-1 (1/√2)

Entonces podemos decir que,

sen(y) = (1/√2)

Sabemos que el rango de la rama de valor principal de sin ^-1 (x) es (−π/2, π/2) y sin(π/4) = 1/√2.

Entonces, el valor principal de sin ^-1 (1/√2) = π/4.

Problema 2: Encuentra el valor principal de la ecuación dada:

y = sen ^-1 (1)

Solución:

Se nos da que:

y = sen ^-1 (1)

Entonces podemos decir que,

sen(y) = 1

Sabemos que el rango de la rama de valor principal de sin ^-1 (x) es (−π/2, π/2) y sin(π/2) = 1.

Entonces, el valor principal de sin ^-1 (1) = π/2.

Función inversa de coseno, y = cos ^-1 (x)

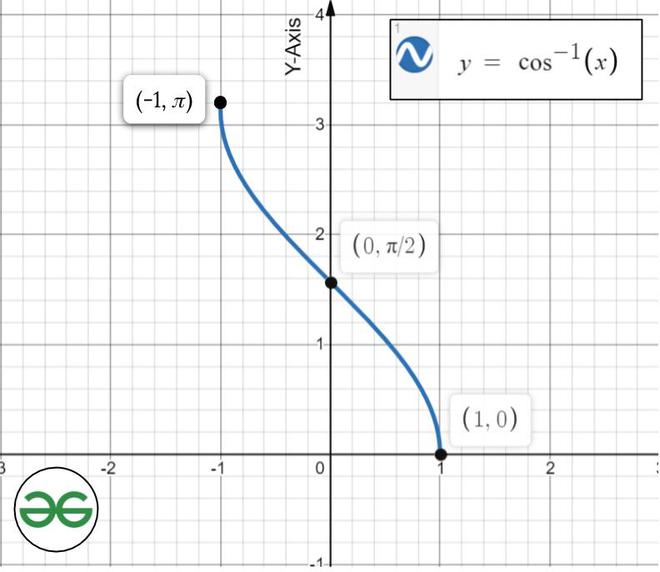
cos ^-1 (x) es la función inversa de cos (x). Su dominio es [−1, 1] y su rango es [0, π]. Se cruza con el eje de coordenadas en (1, π/2). No es ni par ni impar y es estrictamente decreciente en (-1, 1).

Gráfica de función

Análisis de funciones

Dominio	$x ∈ [−1, 1]$
Rango	$y ∈ [0, \pi]$
X-intersección	$x = 1$
Y – Intercepción	$y = \frac{\pi}{2}$
Mínimos	$(1, 0)$
Máxima	$(-1, \pi)$
Puntos de inflexión	$\big(0, \frac{\pi}{2}\big)$
Paridad	Ni Par Ni Impar
monotonicidad	En (-1, 1) estrictamente decreciente

Ejemplos de problemas sobre la función del coseno inverso

Problema 1: Encuentra el valor principal de la ecuación dada:

y = cos ^-1 (1/√2)

Solución:

Se nos da que:

y = cos ^-1 (1/√2)

Entonces podemos decir que,

cos(y) = (1/√2)

Sabemos que el rango de la rama de valor principal de cos ^-1 (x) es (0, π) y cos(π/4) = 1/√2.

Entonces, el valor principal de cos ^-1 (1/√2) = π/4.

Problema 2: Encuentra el valor principal de la ecuación dada:

y = cos ^-1 (1)

Solución:

Se nos da que:

y = cos ^-1 (1)

Entonces podemos decir que,

cos(y) = 1

Sabemos que el rango de la rama de valor principal de cos ^-1 (x) es (0, π) y cos(0)=1.

Entonces, el valor principal de cos ^-1 (1) = 0.

Inversa de la función tangente, y = tan ^-1 (x)

tan ^-1 (x) es la función inversa de tan(x). Su dominio es ℝ y su rango es [-π/2, π/2]. Se cruza con el eje de coordenadas en (0, 0). Es una función impar estrictamente creciente en (-∞, ∞).

Gráfica de función

Análisis de funciones

Dominio	$x ∈ ℝ$
Rango	$y ∈ \big(\frac{-\pi}{2}, \frac{\pi}{2}\big)$
X-intersección	$x = 0$
Y – Intercepción	$y = 0$
Mínimos	La función no tiene puntos mínimos.
Máxima	La función no tiene puntos máximos.
Puntos de inflexión	$(0, 0)$
Paridad	Función impar
monotonicidad	En (−∞, ∞) estrictamente creciente
Asíntotas	$y = \frac{\pi}{2}\space and\space y= \frac{-\pi}{2}$

Ejemplos de problemas sobre la inversa de la función tangente

Problema 1: Encuentra el valor principal de la ecuación dada:

y = bronceado ^-1 (1)

Solución:

Se nos da que:

y = bronceado ^-1 (1)

Entonces podemos decir que,

tan(y) = (1)

Sabemos que el rango de la rama de valor principal de tan ^-1 (x) es (-π/2, π/2) y tan(π/4) = 1.

Entonces, el valor principal de tan ^-1 (1) = π/4.

Problema 2: Encuentra el valor principal de la ecuación dada:

y = bronceado ^-1 (√3)

Solución:

Se nos da que:

y = bronceado ^-1 (√3)

Entonces podemos decir que,

tan(y) = (√3)

Sabemos que el rango de la rama de valor principal de tan-1(x) es (-π/2, π/2) y tan(π/3) = √3.

Entonces, el valor principal de tan-1(√3) = π/3.

Función inversa de cosecante, y = cosec ^-1 (x)

cosec ^-1 (x) es la función inversa de cosec(x). Su dominio es (-∞, -1] U [1, ∞) y su rango es [-π/2, 0) U (0, π/2]. No intercepta el eje de coordenadas. Es un impar función estrictamente decreciente en su dominio.

Gráfica de función

Análisis de funciones

y ∈ \big[\frac{-\pi}{2}, 0 \big) ∪ \big(0, \frac{\pi}{2}\big]

Dominio	$x ∈ (−\infin, −1] ∪ [1,\infin)$
Rango	$y ∈ \big[\frac{-\pi}{2}, 0 \big) ∪ \big(0, \frac{\pi}{2}\big]$
X-intersección	$\phi$
Y – Intercepción	$\phi$
Mínimos	$\big(-1, \frac{-\pi}{2} \big)$
Máxima	$\big(1, \frac{\pi}{2} \big)$
Puntos de inflexión	La función no tiene puntos de inflexión.
Paridad	Función impar
monotonicidad	En (1, ∞) es decreciente y en (-∞, -1) es decreciente
Asíntotas	y = 0

Ejemplos de problemas sobre la función cosecante inversa

Problema 1: Encuentra el valor principal de la ecuación dada:

y = cosec ^-1 (√2)

Solución:

Se nos da que:

y = cosec ^-1 (√2)

Entonces podemos decir que,

cosec(y) = (√2)

Sabemos que el rango de la rama de valor principal de cosec ^-1 (x) es [-π/2, π/2] – {0} y cosec(π/4) = √2.

Entonces, el valor principal de cosec ^-1 (√2) = π/4.

Problema 2: Encuentra el valor principal de la ecuación dada:

y = cosec ^-1 (1)

Solución:

Se nos da que:

y = cosec ^-1 (√2)

Entonces podemos decir que,

cosec(y) = 1

Sabemos que el rango de la rama de valor principal de cosec ^-1 (x) es [-π/2, π/2] – {0} y cosec(π/2) = 1.

Entonces, el valor principal de cosec ^-1 (1) = π/2.

Función inversa de la secante, y = sec ^-1 (x)

sec ^-1 (x) es la función inversa de sec(x). Su dominio es (-∞, -1] U [1, ∞) y su rango es [0, π/2) U (π/2, π]. No intercepta el eje de coordenadas ya que es una función discontinua No es función ni par ni impar y es estrictamente creciente en su dominio.

Gráfica de función

Análisis de funciones

y ∈ \big[0, \frac{\pi}{2}\big) ∪ \big(\frac{\pi}{2}, \pi\big]

Dominio	$x ∈ (−\infin, −1] ∪ [1, \infin)$
Rango	$y ∈ \big[0, \frac{\pi}{2}\big) ∪ \big(\frac{\pi}{2}, \pi\big]$
X-intersección	$x=1$
Y – Intercepción	$\phi$
Mínimos	$(1,0)$
Máxima	$(-1, \pi)$
Puntos de inflexión	La función no tiene puntos de inflexión.
Paridad	Ni Par Ni Impar
monotonicidad	En (1, ∞) es creciente y en (-∞, -1) es creciente
Asíntotas	$y = \frac{\pi}{2}$

Ejemplos de problemas sobre la inversa de la función secante

Problema 1: Encuentra el valor principal de la ecuación dada:

y = seg ^-1 (√2)

Solución:

Se nos da que:

y = seg ^-1 (√2)

Entonces podemos decir que,

segundo(y) = (√2)

Sabemos que el rango de la rama de valor principal de sec ^-1 (x) es [0, π] – {π/2} y sec(π/4)=√2.

Entonces, el valor principal de sec ^-1 (√2) = π/4.

Problema 2: Encuentra el valor principal de la ecuación dada:

y = seg ^-1 (1)

Solución:

Se nos da que:

y = seg ^-1 (1)

Entonces podemos decir que,

segundo(y) = 1

Sabemos que el rango de la rama de valor principal de sec ^-1 (x) es [0, π] – {π/2} y sec(0) = 1.

Entonces, el valor principal de sec ^-1 (1) = 0.

Función inversa de la cotangente, y = cot ^-1 (x)

cot ^-1 (x) es la función inversa de cot(x). Su dominio es ℝ y su rango es (0, π). Se cruza con el eje de coordenadas en (0, π/2). No es una función ni par ni impar y es estrictamente decreciente en su dominio.

Gráfica de función

Análisis de funciones

Dominio	$x ∈ ℝ$
Rango	$y ∈ (0, \pi)$
X-intersección	$x = 0$
Y – Intercepción	$y = \frac{\pi}{2}$
Mínimos	La función no tiene puntos mínimos.
Máxima	La función no tiene puntos máximos.
Puntos de inflexión	La función no tiene puntos de inflexión.
Paridad	Ni Par Ni Impar
monotonicidad	En (-∞, ∞) estrictamente decreciente
Asíntotas	$y = 0\space and\space y = \pi$

Ejemplos de problemas sobre la inversa de la función cotangente

Problema 1: Encuentra el valor principal de la ecuación dada:

y = cuna ^-1 (1)

Solución:

Se nos da que:

y = cuna ^-1 (1)

Entonces podemos decir que,

cuna(y) = 1

Sabemos que el rango de la rama de valor principal de cot ^-1 (x) es (-π/2, π/2) y cot(π/4) = 1.

Entonces, el valor principal de cot ^-1 (1) = π/4.

Problema 2: Encuentra el valor principal de la ecuación dada:

y = cuna ^-1 (1/√3)

Solución:

Se nos da que:

y = cuna ^-1 (1/√3)

Entonces podemos decir que,

cuna(y) = (1/√3)

Sabemos que el rango de la rama de valor principal de cot ^-1 (x) es (-π/2, π/2) y cot(π/3)= 1/√3.

Entonces, el valor principal de cot ^-1 (1/√3) = π/3.

Publicación traducida automáticamente

Artículo escrito por aditya_taparia y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Gráficas de Funciones Trigonométricas Inversas – Trigonometría | Clase 12 Matemáticas

Función inversa de seno, y = sen ^-1 (x)

Gráfica de función

Análisis de funciones

Problemas de muestra sobre la función del seno inverso

Función inversa de coseno, y = cos ^-1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la función del coseno inverso

Inversa de la función tangente, y = tan ^-1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la inversa de la función tangente

Función inversa de cosecante, y = cosec ^-1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la función cosecante inversa

Función inversa de la secante, y = sec ^-1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la inversa de la función secante

Función inversa de la cotangente, y = cot ^-1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la inversa de la función cotangente

Deja una respuesta Cancelar la respuesta

Función inversa de seno, y = sen -1 (x)

Gráfica de función

Análisis de funciones

Problemas de muestra sobre la función del seno inverso

Función inversa de coseno, y = cos -1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la función del coseno inverso

Inversa de la función tangente, y = tan -1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la inversa de la función tangente

Función inversa de cosecante, y = cosec -1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la función cosecante inversa

Función inversa de la secante, y = sec -1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la inversa de la función secante

Función inversa de la cotangente, y = cot -1 (x)

Gráfica de función

Análisis de funciones

Ejemplos de problemas sobre la inversa de la función cotangente

Deja una respuesta Cancelar la respuesta

Función inversa de seno, y = sen ^-1 (x)

Función inversa de coseno, y = cos ^-1 (x)

Inversa de la función tangente, y = tan ^-1 (x)

Función inversa de cosecante, y = cosec ^-1 (x)

Función inversa de la secante, y = sec ^-1 (x)

Función inversa de la cotangente, y = cot ^-1 (x)