La trigonometría tiene que ver con los triángulos o, para ser más precisos, con la relación entre los ángulos y los lados de un triángulo rectángulo. Hay tres lados de un triángulo llamado hipotenusa, adyacente y opuesto. La relación entre estos lados en función del ángulo entre ellos se denominan relaciones trigonométricas.

Como se indica en la figura en un triángulo rectángulo
- El lado opuesto al ángulo recto se llama hipotenusa
- El lado opuesto a un ángulo se llama lado opuesto
- Para el ángulo C el lado opuesto es AB
- Para el ángulo A el lado opuesto es BC
- El lado adyacente a un ángulo se llama lado adyacente
- Para el ángulo C el lado adyacente es BC
- Para el ángulo A el lado adyacente es AB
Razones trigonométricas
Hay 6 relaciones trigonométricas básicas que forman los fundamentos de la trigonometría. Estas 6 relaciones trigonométricas son proporciones de todas las diferentes combinaciones posibles en un triángulo rectángulo.
Estas razones trigonométricas se llaman
- Seno
- Coseno
- Tangente
- Cosecante
- Secante
- Cotangente
El símbolo matemático θ se utiliza para indicar el ángulo.
A. Seno (pecado)
El seno de un ángulo se define por la relación entre las longitudes de los lados opuestos al ángulo y la hipotenusa. Se representa como sen θ

B. Coseno (cos)
El coseno de un ángulo se define por la relación entre las longitudes de los lados adyacentes al ángulo y la hipotenusa. Se representa como cos θ

C. Tangente (bronceado)
La tangente de un ángulo se define por la relación entre la longitud de los lados opuestos al ángulo y el lado adyacente al ángulo. Se representa como tan θ

D. Cosecante (csc)
La cosecante de un ángulo se define por la relación entre la longitud de la hipotenusa y el lado opuesto al ángulo. Se representa como csc θ

E. secante (seg)
La secante de un ángulo se define por la relación entre la longitud de la hipotenusa y el lado y el lado adyacente al ángulo. Se representa como sec θ

F. Cotangente (cuna)
La cotangente de un ángulo se define por la relación entre la longitud de los lados adyacentes al ángulo y el lado opuesto al ángulo. Se representa como cuna θ.

Tabla trigonométrica
|
Relación trigonométrica |
Abreviatura |
Fórmula |
|
seno |
pecado |
Opuesto/Hipotenusa |
|
coseno |
porque |
Adyacente/Hipotenusa |
|
tangente |
broncearse |
Opuesto/Adyacente |
|
cosecante |
csc |
Hipotenusa/Opuesto |
|
secante |
segundo |
Hipotenusa/Adyacente |
|
cotangente |
cuna |
Adyacente/Opuesto |
Tabla trigonométrica para ángulos específicos:
| Anglos | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| pecado | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| porque | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| broncearse | 0 | 1/√3 | 1 | √3 | No definida |
| cosec | No definida | 2 | √2 | 2/√3 | 1 |
| segundo | 1 | 2/√3 | √2 | 2 | No definida |
| cuna | No definida | √3 | 1 | 1/√3 | 0 |
Resolver un lado en triángulos rectángulos con trigonometría
Este es uno de los usos más básicos y útiles de la trigonometría usando las razones trigonométricas mencionadas es encontrar la longitud de un lado de un triángulo rectángulo. Pero para hacerlo, entonces ya debemos saber la longitud de los otros dos lados o un ángulo. y longitud de un lado.
Pasos a seguir si se conocen un lado y un ángulo:
- Elige una razón trigonométrica que contenga el lado dado y el lado desconocido
- Usa el álgebra para encontrar el lado desconocido
Ejemplo:
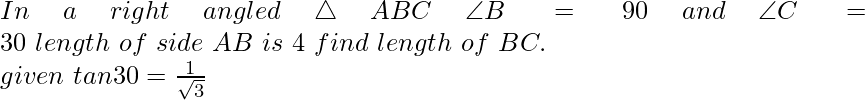

Solución:

Pasos a seguir si se conocen dos lados:
- Marque los lados conocidos como adyacentes, opuestos o hipotenusas con respecto a cualquiera de los ángulos agudos del triángulo.
- Decide qué relación trigonométrica se puede encontrar en la tabla anterior.
- Encuentra el ángulo (X)
- Usa una razón trigonométrica con respecto a X que es una razón de un lado conocido y un lado desconocido.
- Usa el álgebra para encontrar el lado desconocido.
Ejemplo:
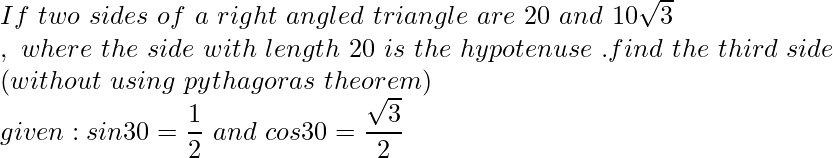
Solución:

Publicación traducida automáticamente
Artículo escrito por somsagar2019 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA