Dado un gráfico y un vértice de origen en el gráfico, encuentre los caminos más cortos desde el origen hasta todos los vértices en el gráfico dado.
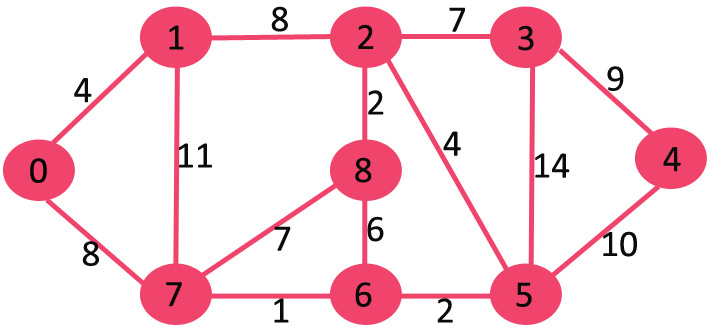
Input : Source = 0
Output :
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
Hemos discutido las implementaciones de ruta más corta de Dijkstra.
- Algoritmo de Dijkstra para la representación de arrays de adyacencia (en C/C++ con complejidad temporal O(v 2 )
- Algoritmo de Dijkstra para la representación de listas de adyacencia (en C con complejidad temporal O (ELogV))
La segunda implementación es mejor en cuanto a la complejidad del tiempo, pero es realmente compleja ya que hemos implementado nuestra propia cola de prioridad. STL proporciona la cola de prioridad , pero la cola de prioridad proporcionada no admite las operaciones de eliminación y reducción de clave. Y en el algoritmo de Dijkstra, necesitamos una cola de prioridad y las siguientes operaciones en la cola de prioridad:
- ExtractMin: de todos aquellos vértices cuya distancia más corta aún no se encuentra, necesitamos obtener el vértice con la distancia mínima.
- DecreaseKey: después de extraer el vértice, necesitamos actualizar la distancia de sus vértices adyacentes, y si la nueva distancia es más pequeña, actualícela en la estructura de datos.
Las operaciones anteriores se pueden implementar fácilmente mediante la estructura de datos establecida de c ++ STL , el conjunto mantiene todas sus claves ordenadas, por lo que el vértice distante mínimo siempre estará al principio, podemos extraerlo desde allí, que es la operación ExtractMin y actualizar otro vértice adyacente en consecuencia si la distancia de cualquier vértice se vuelve más pequeña, elimine su entrada anterior e inserte una nueva entrada actualizada que es la operación DecreaseKey.
A continuación se muestra el algoritmo basado en la estructura de datos establecida.
1) Initialize distances of all vertices as infinite. 2) Create an empty set. Every item of set is a pair (weight, vertex). Weight (or distance) is used as first item of pair as first item is by default used to compare two pairs. 3) Insert source vertex into the set and make its distance as 0. 4) While Set doesn't become empty, do following a) Extract minimum distance vertex from Set. Let the extracted vertex be u. b) Loop through all adjacent of u and do following for every vertex v. // If there is a shorter path to v // through u. If dist[v] > dist[u] + weight(u, v) (i) Update distance of v, i.e., do dist[v] = dist[u] + weight(u, v) (i) If v is in set, update its distance in set by removing it first, then inserting with new distance (ii) If v is not in set, then insert it in set with new distance 5) Print distance array dist[] to print all shortest paths.
A continuación se muestra la implementación en C++ de la idea anterior.
C++
// Program to find Dijkstra's shortest path using STL set
#include<bits/stdc++.h>
using namespace std;
# define INF 0x3f3f3f3f
// This class represents a directed graph using
// adjacency list representation
class Graph
{
int V; // No. of vertices
// In a weighted graph, we need to store vertex
// and weight pair for every edge
list< pair<int, int> > *adj;
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int u, int v, int w);
// prints shortest path from s
void shortestPath(int s);
};
// Allocates memory for adjacency list
Graph::Graph(int V)
{
this->V = V;
adj = new list< pair<int, int> >[V];
}
void Graph::addEdge(int u, int v, int w)
{
adj[u].push_back(make_pair(v, w));
adj[v].push_back(make_pair(u, w));
}
// Prints shortest paths from src to all other vertices
void Graph::shortestPath(int src)
{
// Create a set to store vertices that are being
// processed
set< pair<int, int> > setds;
// Create a vector for distances and initialize all
// distances as infinite (INF)
vector<int> dist(V, INF);
// Insert source itself in Set and initialize its
// distance as 0.
setds.insert(make_pair(0, src));
dist[src] = 0;
/* Looping till all shortest distance are finalized
then setds will become empty */
while (!setds.empty())
{
// The first vertex in Set is the minimum distance
// vertex, extract it from set.
pair<int, int> tmp = *(setds.begin());
setds.erase(setds.begin());
// vertex label is stored in second of pair (it
// has to be done this way to keep the vertices
// sorted distance (distance must be first item
// in pair)
int u = tmp.second;
// 'i' is used to get all adjacent vertices of a vertex
list< pair<int, int> >::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
{
// Get vertex label and weight of current adjacent
// of u.
int v = (*i).first;
int weight = (*i).second;
// If there is shorter path to v through u.
if (dist[v] > dist[u] + weight)
{
/* If distance of v is not INF then it must be in
our set, so removing it and inserting again
with updated less distance.
Note : We extract only those vertices from Set
for which distance is finalized. So for them,
we would never reach here. */
if (dist[v] != INF)
setds.erase(setds.find(make_pair(dist[v], v)));
// Updating distance of v
dist[v] = dist[u] + weight;
setds.insert(make_pair(dist[v], v));
}
}
}
// Print shortest distances stored in dist[]
printf("Vertex Distance from Source\n");
for (int i = 0; i < V; ++i)
printf("%d \t\t %d\n", i, dist[i]);
}
// Driver program to test methods of graph class
int main()
{
// create the graph given in above figure
int V = 9;
Graph g(V);
// making above shown graph
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.shortestPath(0);
return 0;
}
Vertex Distance from Source 0 0 1 4 2 12 3 19 4 21 5 11 6 9 7 8 8 14
Complejidad de tiempo: los conjuntos en C++ se implementan normalmente mediante árboles de búsqueda binarios autoequilibrados. Por lo tanto, la complejidad temporal de las operaciones de configuración como insertar, eliminar es logarítmica y la complejidad temporal de la solución anterior es O(ELogV)).
Algoritmo de ruta más corta de Dijkstra usando la cola de prioridad de STL Este artículo es una contribución de Utkarsh Trivedi .
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA