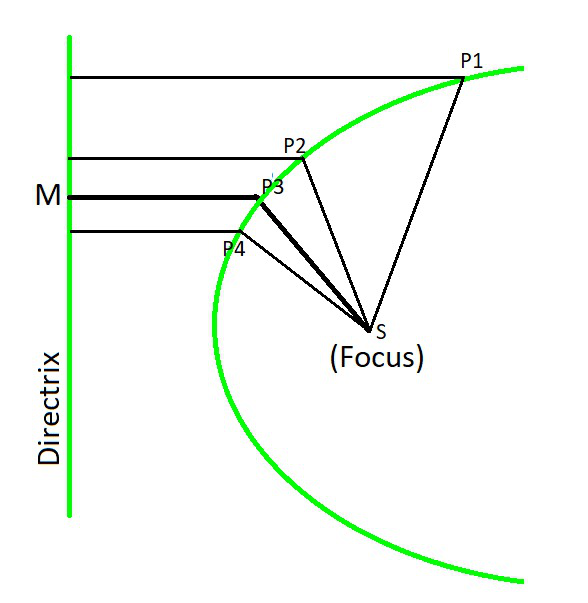
En matemáticas, una parábola es el lugar geométrico de un punto que se mueve en un plano donde su distancia desde un punto fijo conocido como foco es siempre igual a la distancia desde una línea recta fija conocida como directriz en el mismo plano. O en otras palabras, una parábola es una curva plana que tiene casi forma de U donde cada punto es equidistante de un punto fijo conocido como foco y la línea recta conocida como directriz. La parábola tiene un solo foco y el foco nunca se encuentra en la directriz. Como se muestra en el siguiente diagrama, donde P 1 M = P 1 S, P 2 M = P 2 S, P 3 M = P 3 S y P 4 M = P 4 S.
Ecuación de la parábola a partir del foco y la directriz
Ahora aprenderemos a encontrar la ecuación de la parábola a partir del foco y la directriz. Entonces, sea S el foco y la línea ZZ’ la directriz. Dibuja SK perpendicular desde S en la directriz y biseca SK en V. Luego,
VS = VK
La distancia de V desde el foco = Distancia de V desde la directriz
V se encuentra en la parábola, Entonces, SK = 2a.
Entonces, VS = VK = a
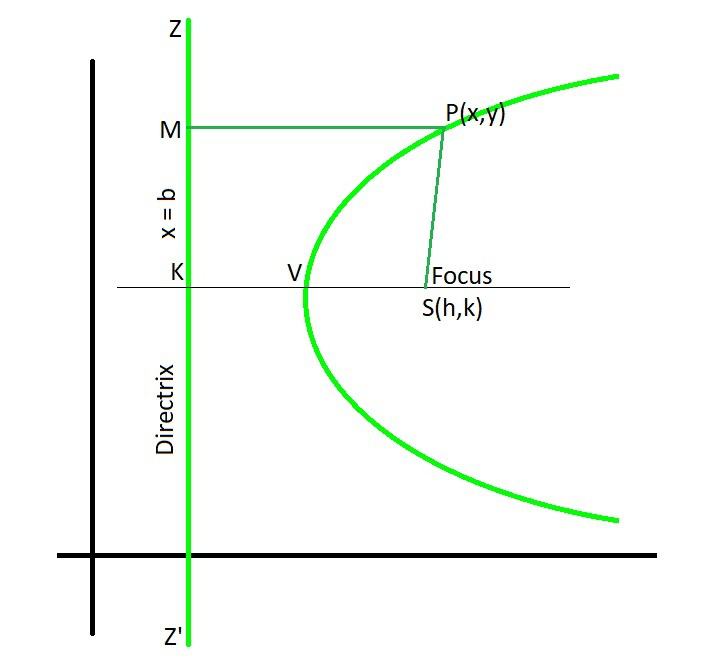
Tomemos V como vértice, VK es una recta perpendicular a ZZ’ y paralela al eje x. Entonces, las coordenadas del foco S son (h, k) y la ecuación de la directriz ZZ’ es x = b. PM es perpendicular a la directriz x = b y el punto M será (b, y)
Consideremos un punto P(x, y) sobre la parábola. Ahora, únete a SP y PM.
Como sabemos que P se encuentra en la parábola
Entonces, SP = PM (definición de parábola)
SP 2 = PM 2
(x – h) 2 + (y – k) 2 = (x – b) 2 + (y – y) 2
x 2 – 2hx + h 2 + (yk) 2 = x 2 – 2bx + b 2
Suma (2hx – b 2 ) en ambos lados, obtenemos
x 2 – 2hx + h 2 + 2hx – b 2 + (yk) 2 = x 2 – 2bx + b 2 + 2hx – b 2
2(h – b)x = (yk) 2 + h 2 – b 2
Divida la ecuación por 2(h – b), obtenemos
x = ![]()
x =
………………..(1)
De manera similar, cuando la directriz y = b, obtenemos
y =
………………..(2)
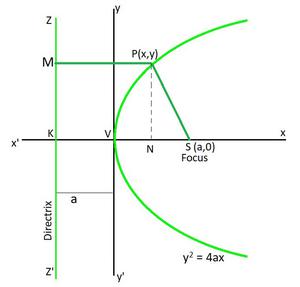
Cuando V es el origen, VS como eje x de longitud a. Entonces, las coordenadas de S serán (a, 0), y la directriz ZZ’ es x = -a.
h = a, k = 0 y b = -a
Usando la ecuación (1), obtenemos
x = ![]()
x = ![]()
y2 = 4ax
Es la ecuación estándar de la parábola.
Nota: La parábola tiene dos focos reales situados en su eje, uno de los cuales es el foco S y el otro se encuentra en el infinito. La directriz correspondiente también está en el infinito.
Trazado de la parábola y 2 = 4ax, a>0
La ecuación dada se puede escribir como y = ± 2 ![]() , observamos los siguientes puntos de la ecuación:
, observamos los siguientes puntos de la ecuación:
- Simetría : la ecuación dada establece que por cada valor positivo de x, hay dos valores iguales y opuestos de y.
- Región : la ecuación dada establece que para cada valor negativo de x, el valor de y es imaginario, lo que significa que ninguna parte de la curva se encuentra a la izquierda del eje y.
- Origen : El origen es el punto por donde pasa la curva y la tangente en el origen es x = 0, es decir, el eje y.
- Porción ocupada : Como x⇢∞, y⇢∞. Por lo tanto, la curva se extiende hasta el infinito a la derecha del eje de y.
Algunas otras formas estándar de la parábola con foco y directriz.
La forma más simple de la ecuación de la parábola es cuando el vértice está en el origen y el eje de simetría está junto con el eje x o el eje y. Estos tipos de parábolas son:
1. y2 = 4ax
Aquí,
- Coordenadas del vértice: (0, 0)
- Coordenadas de foco: (a, 0)
- Ecuación de la directriz: x = -a
- Ecuación del eje: y = 0
- Longitud del latus rectum: 4a
- Distancia focal de un punto P(x, y): a + x
2. x 2 = 4 días

Aquí,
- Coordenadas del vértice: (0, 0)
- Coordenadas de foco: (-a, 0)
- Ecuación de la directriz: x = a
- Ecuación del eje: y = 0
- Longitud del latus rectum: 4a
- Distancia focal de un punto P(x, y): a – x
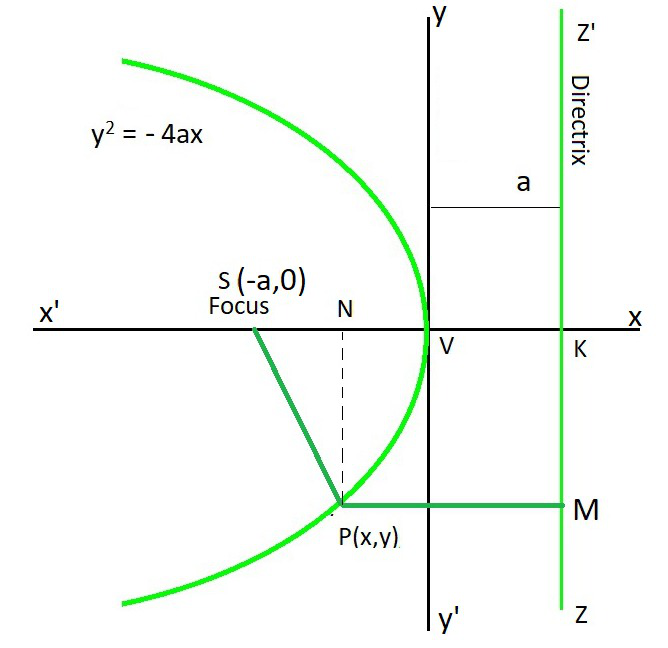
3. y 2 = – 4 día
Aquí,
- Coordenadas del vértice: (0, 0)
- Coordenadas de foco: (0, a)
- Ecuación de la directriz: y = -a
- Ecuación del eje: x = 0
- Longitud del latus rectum: 4a
- Distancia focal de un punto P(x, y): a + y
4. x 2 = – 4 día

Aquí,
- Coordenadas del vértice: (0, 0)
- Coordenadas de foco: (0, -a)
- Ecuación de la directriz: y = a
- Ecuación del eje: x = 0
- Longitud del latus rectum: 4a
- Distancia focal de un punto P(x, y): a – y
Problemas de muestra
Pregunta 1. Encuentra la ecuación de la parábola cuyo foco es (-4, 2) y la directriz es x + y = 3.
Solución:
Sea P (x, y) cualquier punto de la parábola cuyo foco sea (-4, 2) y la directriz x + y – 3 = 0.
Como ya sabemos que la distancia de un punto P al foco = distancia de un punto P a la directriz
Entonces, √(x + 4) 2 + (y – 2) 2 =
Al elevar al cuadrado ambos lados obtenemos
(x + 4) 2 + (y – 2) 2 =
2 ((x2 + 16 + 8x) + ( y2 + 4 – 4y)) = x2 + y2 + 9 +2xy – 6x – 6y
2 (x2 + 20 + 8x + y2 – 4y) = x2 + y2 + 9 +2xy – 6x – 6y
2x 2 + 40 + 16x + 2y 2 – 8y = x 2 + y 2 + 9 +2xy – 6x – 6y
x2 + y2 + 2xy + 10x – 2y + 31 = 0
Pregunta 2. Encuentra la ecuación de la parábola cuyo foco es (-4, 0) y la directriz x + 6 = 0.
Solución:
Sea P (x, y) cualquier punto de la parábola cuyo foco sea (-4, 0) y la directriz x + 6 = 0.
Como ya sabemos que la distancia de un punto P al foco = distancia de un punto P a la directriz
Entonces, √(x + 4) 2 + (y ) 2 =
Al elevar al cuadrado ambos lados obtenemos
(x + 4) 2 + (y) 2 =
2x 2 + 32 + 16x + 2y 2 = x 2 + 36 + 12x
x 2 + 2y 2 – 4 + 14x = 0
Pregunta 3. Encuentra la ecuación de la parábola con foco (4, 0) y directriz x = – 3.
Solución:
Dado que el foco (4, 0) se encuentra en el eje x, el propio eje x es el eje de la parábola.
Por lo tanto, la ecuación de la parábola es de la forma
y 2 = 4ax o y 2 = – 4ax.
Como la directriz es x = – 3 y el foco es (4, 0),
la parábola debe ser de la forma y 2 = 4ax con a = 4.
Por lo tanto, la ecuación requerida es
y2 = 4(4) x
y2 = 16x
Pregunta 4. Encuentra la ecuación de la parábola con vértice en (0, 0) y foco en (0, 4).
Solución:
Dado que el vértice está en (0, 0) y el foco está en (0, 5), que se encuentra en el eje y, el eje y es el eje de la parábola.
Por lo tanto, la ecuación de la parábola es x 2 = 4ay.
Por lo tanto, tenemos x 2 = 4(4)y, es decir,
x2 = 16y
Foco y directriz de una parábola de la ecuación
Ahora aprenderemos cómo encontrar el foco y la directriz de una parábola a partir de la ecuación.

Entonces, cuando la ecuación de una parábola es
y – k = a(x – h) 2
Aquí, el valor de a = 1/4C
Entonces el foco es (h, k + C), el vértice es (h, k) y la directriz es y = k – C.
Ejemplos de muestra
Pregunta 1. y 2 = 8x
Solución:
La parábola dada es de la forma y 2 = 4ax, donde
4a = 8
un = 2
Las coordenadas del foco son (a,0), es decir (2,0)
y, la ecuación de la directriz es
x = -a, es decir, x = -2
Pregunta 2. y 2 – 8y – x + 19 = 0
Solución:
Reordenando, obtenemos
y 2 – 8y + 16 – x + 3 = 0
y 2 – 8y + 16 = x – 3
x = (y-4) 2 + 3
Comparando con la ecuación (1), concluimos
k = 4
2(hb) = 1 ……………(I)
= 3 ……………(II)
Resolviendo (I) y (II), obtenemos
h =
y b =
Por lo tanto, Foco es (h,k) = (
,4)
y, directriz x = b =
Pregunta 3. Encuentra el foco, la directriz y el vértice de la siguiente ecuación: y = x 2 – 2x + 3
Solución:
Reordenando, obtenemos
y =x 2 – 2x + 4 – 1
y =(x-1) 2 + 2
Comparando con la ecuación (4), concluimos
h = 1
y 1 = 2
2(kb) = 1 ……………(yo)
= 2 ……………(II)
Resolviendo (I) y (II), obtenemos
k =
y b =
Por lo tanto, Foco es (h,k) = ( 1,
),
directriz y = b =
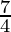
y, vértice (h, y 1 ) = (1,2)
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA