Dados tres números n, r y p, calcule el valor de n C r mod p.
Ejemplo:
Input: n = 10, r = 2, p = 13 Output: 6 Explanation: 10C2 is 45 and 45 % 13 is 6.
Le recomendamos encarecidamente que haga clic aquí y lo practique antes de pasar a la solución.
MÉTODO 1: (Usando Programación Dinámica)
Una solución simple es calcular primero n C r , luego calcular n C r % p. Esta solución funciona bien cuando el valor de n C r es pequeño.
¿Qué pasa si el valor de n C r es grande?
El valor de n C r %p generalmente se necesita para valores grandes de n cuando n C r no cabe en una variable y provoca un desbordamiento. Calculando n C ry luego usar un operador modular no es una buena idea ya que habrá un desbordamiento incluso para valores ligeramente mayores de n y r. Por ejemplo, los métodos discutidos aquí y aquí causan un desbordamiento para n = 50 y r = 40.
La idea es calcular n C r usando la siguiente fórmula
C(n, r) = C(n-1, r-1) + C(n-1, r) C(n, 0) = C(n, n) = 1
Funcionamiento de la fórmula anterior y el Triángulo de Pascal:
Veamos cómo funciona la fórmula anterior para C(4, 3)
1==========>> n = 0, C(0, 0) = 1
1–1 ========>> n = 1, C(1, 0) = 1, C(1, 1) = 1
1–2–1======>> n = 2, C( 2, 0) = 1, C(2, 1) = 2, C(2, 2) = 1
1–3–3–1====>> n = 3, C(3, 0) = 1, C(3, 1) = 3, C(3, 2) = 3, C(3, 3)=1
1–4–6–4–1==>> n = 4, C(4, 0) = 1, C(4, 1) = 4, C(4, 2) = 6, C(4, 3)=4, C(4, 4)=1
Así que aquí cada ciclo en i, construye la i-ésima fila de triángulo pascal, usando (i-1) fila
Extensión de la fórmula anterior para la aritmética modular:
Podemos usar la propiedad distributiva del operador modular para encontrar nCr % p usando la fórmula anterior.
C(n, r)%p = [ C(n-1, r-1)%p + C(n-1, r)%p ] % p C(n, 0) = C(n, n) = 1
La fórmula anterior se puede implementar usando Programación Dinámica usando una array 2D.
La solución de programación dinámica basada en array 2D se puede optimizar aún más mediante la construcción de una fila a la vez. Consulte la versión optimizada para el espacio en la publicación a continuación para obtener más detalles.
Coeficiente binomial usando programación dinámica
A continuación se muestra la implementación basada en la versión optimizada de espacio discutida en la publicación anterior.
C++
// A Dynamic Programming based solution to compute nCr % p
#include <bits/stdc++.h>
using namespace std;
// Returns nCr % p
int nCrModp(int n, int r, int p)
{
// Optimization for the cases when r is large
if (r > n - r)
r = n - r;
// The array C is going to store last row of
// pascal triangle at the end. And last entry
// of last row is nCr
int C[r + 1];
memset(C, 0, sizeof(C));
C[0] = 1; // Top row of Pascal Triangle
// One by constructs remaining rows of Pascal
// Triangle from top to bottom
for (int i = 1; i <= n; i++) {
// Fill entries of current row using previous
// row values
for (int j = min(i, r); j > 0; j--)
// nCj = (n-1)Cj + (n-1)C(j-1);
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
// Driver program
int main()
{
int n = 10, r = 2, p = 13;
cout << "Value of nCr % p is " << nCrModp(n, r, p);
return 0;
}
JAVA
// A Dynamic Programming based
// solution to compute nCr % p
import java.io.*;
import java.util.*;
import java.math.*;
class GFG {
// Returns nCr % p
static int nCrModp(int n, int r, int p)
{
if (r > n - r)
r = n - r;
// The array C is going to store last
// row of pascal triangle at the end.
// And last entry of last row is nCr
int C[] = new int[r + 1];
C[0] = 1; // Top row of Pascal Triangle
// One by constructs remaining rows of Pascal
// Triangle from top to bottom
for (int i = 1; i <= n; i++) {
// Fill entries of current row using previous
// row values
for (int j = Math.min(i, r); j > 0; j--)
// nCj = (n-1)Cj + (n-1)C(j-1);
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
// Driver program
public static void main(String args[])
{
int n = 10, r = 2, p = 13;
System.out.println("Value of nCr % p is "
+ nCrModp(n, r, p));
}
}
// This code is contributed by Nikita Tiwari.
Python3
# A Dynamic Programming based solution to compute nCr % p
# Returns nCr % p
def nCrModp(n, r, p):
# Optimization for the cases when r is large
# compared to n-r
if (r > n- r):
r = n - r
# The array C is going to store last row of
# pascal triangle at the end. And last entry
# of last row is nCr.
C = [0 for i in range(r + 1)]
C[0] = 1 # Top row of Pascal Triangle
# One by constructs remaining rows of Pascal
# Triangle from top to bottom
for i in range(1, n + 1):
# Fill entries of current row
# using previous row values
for j in range(min(i, r), 0, -1):
# nCj = (n - 1)Cj + (n - 1)C(j - 1)
C[j] = (C[j] + C[j-1]) % p
return C[r]
# Driver Program
n = 10
r = 2
p = 13
print('Value of nCr % p is', nCrModp(n, r, p))
# This code is contributed by Soumen Ghosh
C#
// A Dynamic Programming based
// solution to compute nCr % p
using System;
class GFG {
// Returns nCr % p
static int nCrModp(int n, int r, int p)
{
// Optimization for the cases when r is large
if (r > n - r)
r = n - r;
// The array C is going to store last
// row of pascal triangle at the end.
// And last entry of last row is nCr
int[] C = new int[r + 1];
for (int i = 0; i < r + 1; i++)
C[i] = 0;
C[0] = 1; // Top row of Pascal Triangle
// One by constructs remaining rows
// of Pascal Triangle from top to bottom
for (int i = 1; i <= n; i++) {
// Fill entries of current row using
// previous row values
for (int j = Math.Min(i, r); j > 0; j--)
// nCj = (n-1)Cj + (n-1)C(j-1);
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
// Driver program
public static void Main()
{
int n = 10, r = 2, p = 13;
Console.Write("Value of nCr % p is "
+ nCrModp(n, r, p));
}
}
// This code is contributed by nitin mittal.
PHP
<?php
// A Dynamic Programming based
// solution to compute nCr % p
// Returns nCr % p
function nCrModp($n, $r, $p)
{
// Optimization for the cases when r is large
if ($r > $n - $r)
$r = $n - $r;
// The array C is going
// to store last row of
// pascal triangle at
// the end. And last entry
// of last row is nCr
$C = array();
for( $i = 0; $i < $r + 1; $i++)
$C[$i] = 0;
// Top row of Pascal
// Triangle
$C[0] = 1;
// One by constructs remaining
// rows of Pascal Triangle from
// top to bottom
for ($i = 1; $i <= $n; $i++)
{
// Fill entries of current
// row using previous row values
for ($j = Min($i, $r); $j > 0; $j--)
// nCj = (n-1)Cj + (n-1)C(j-1);
$C[$j] = ($C[$j] +
$C[$j - 1]) % $p;
}
return $C[$r];
}
// Driver Code
$n = 10; $r = 2;$p = 13;
echo "Value of nCr % p is ",
nCrModp($n, $r, $p);
// This code is contributed
// by anuj_67.
?>
Javascript
<script>
// A Dynamic Programming based
// solution to compute nCr % p
// Returns nCr % p
function nCrModp(n,r,p)
{
if (r > n - r)
r = n - r;
// The array C is going to store last
// row of pascal triangle at the end.
// And last entry of last row is nCr
let C = new Array(r + 1);
for(let i = 0; i < r + 1; i++)
C[i] = 0;
C[0] = 1; // Top row of Pascal Triangle
// One by constructs remaining rows of Pascal
// Triangle from top to bottom
for (let i = 1; i <= n; i++) {
// Fill entries of current row using previous
// row values
for (let j = Math.min(i, r); j > 0; j--)
// nCj = (n-1)Cj + (n-1)C(j-1);
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
// Driver program
let n = 10, r = 2, p = 13;
document.write("Value of nCr % p is "
+ nCrModp(n, r, p));
// This code is contributed by avanitrachhadiya2155
</script>
Value of nCr % p is 6
La complejidad temporal de la solución anterior es O(n*r) y requiere espacio O(r). Hay más y mejores soluciones al problema anterior.
Calcule nCr % p | Conjunto 2 (Teorema de Lucas)
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
MÉTODO 2 (usando Pascal Triangle y Dynamic Pro)
Otro enfoque consiste en utilizar el concepto del Triángulo de Pascal. En lugar de calcular el valor de n C r para cada n a partir de n=0 hasta n=n, el enfoque apunta a usar la fila n para el cálculo. El método avanza encontrando una relación general entre n C r y n C r-1 .
FORMULA: C(n,r)=C(n,r-1)* (n-r+1)/r Example: For instance, take n=5 and r=3. Input: n = 5, r = 3, p = 1000000007 Output: 6 Explanation: 5C3 is 10 and 10 % 100000007 is 10. As per the formula, C(5,3)=5!/(3!)*(2!) C(5,3)=10 Also, C(5,2)=5!/(2!)*(3!) C(5,2)=10 Let's try applying the above formula. C(n,r)=C(n,r-1)* (n-r+1)/r C(5,3)=C(5,2)*(5-3+1)/3 C(5,3)=C(5,2)*1 C(5,3)=10*1
El ejemplo anterior muestra que C(n,r) se puede calcular fácilmente calculando C(n,r-1) y multiplicando el resultado por el término (n-r+1)/r. Pero esta multiplicación puede causar un desbordamiento de enteros para valores grandes de n. Para abordar esta situación, utilice los conceptos de multiplicación de módulo y división de módulo para lograr optimizaciones en términos de desbordamiento de enteros.
Averigüemos cómo construir Pascal Triangle para el mismo.
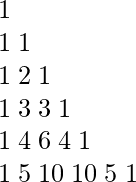
La declaración de array 1D se puede optimizar aún más con solo la declaración de una sola variable para realizar cálculos. Sin embargo, el desbordamiento de enteros también exige otras funciones para la implementación final.
La publicación a continuación menciona la implementación optimizada de espacio y tiempo para el cálculo del coeficiente binario.
C++
// C++ program to find the nCr%p
// based on optimal Dynamic
// Programming implementation and
// Pascal Triangle concepts
#include <bits/stdc++.h>
using namespace std;
// Returns (a * b) % mod
long long moduloMultiplication(long long a, long long b,
long long mod)
{
// Initialize result
long long res = 0;
// Update a if it is more than
// or equal to mod
a %= mod;
while (b) {
// If b is odd, add a with result
if (b & 1)
res = (res + a) % mod;
// Here we assume that doing 2*a
// doesn't cause overflow
a = (2 * a) % mod;
b >>= 1; // b = b / 2
}
return res;
}
// C++ function for extended Euclidean Algorithm
long long int gcdExtended(long long int a, long long int b,
long long int* x,
long long int* y);
// Function to find modulo inverse of b. It returns
// -1 when inverse doesn't exists
long long int modInverse(long long int b, long long int m)
{
long long int x, y; // used in extended GCD algorithm
long long int g = gcdExtended(b, m, &x, &y);
// Return -1 if b and m are not co-prime
if (g != 1)
return -1;
// m is added to handle negative x
return (x % m + m) % m;
}
// C function for extended Euclidean Algorithm (used to
// find modular inverse.
long long int gcdExtended(long long int a, long long int b,
long long int* x,
long long int* y)
{
// Base Case
if (a == 0) {
*x = 0, *y = 1;
return b;
}
// To store results of recursive call
long long int x1, y1;
long long int gcd = gcdExtended(b % a, a, &x1, &y1);
// Update x and y using results of recursive
// call
*x = y1 - (b / a) * x1;
*y = x1;
return gcd;
}
// Function to compute a/b under modulo m
long long int modDivide(long long int a, long long int b,
long long int m)
{
a = a % m;
long long int inv = modInverse(b, m);
if (inv == -1)
// cout << "Division not defined";
return 0;
else
return (inv * a) % m;
}
// Function to calculate nCr % p
int nCr(int n, int r, int p)
{
// Edge Case which is not possible
if (r > n)
return 0;
// Optimization for the cases when r is large
if (r > n - r)
r = n - r;
// x stores the current result at
long long int x = 1;
// each iteration
// Initialized to 1 as nC0 is always 1.
for (int i = 1; i <= r; i++) {
// Formula derived for calculating result is
// C(n,r-1)*(n-r+1)/r
// Function calculates x*(n-i+1) % p.
x = moduloMultiplication(x, (n + 1 - i), p);
// Function calculates x/i % p.
x = modDivide(x, i, p);
}
return x;
}
// Driver Code
int main()
{
long long int n = 5, r = 3, p = 1000000007;
cout << "Value of nCr % p is " << nCr(n, r, p);
return 0;
}
Python3
# Python3 program to find the nCr%p
# based on optimal Dynamic
# Programming implementation and
# Pascal Triangle concepts
# Returns (a * b) % mod
def moduloMultiplication(a, b, mod):
# Initialize result
res = 0
# Update a if it is more than
# or equal to mod
a %= mod
while (b):
# If b is odd, add a with result
if (b & 1):
res = (res + a) % mod
# Here we assume that doing 2*a
# doesn't cause overflow
a = (2 * a) % mod
b >>= 1 # b = b / 2
return res
# Global Variables
x, y = 0, 1
# Function for extended Euclidean Algorithm
def gcdExtended(a, b):
global x, y
# Base Case
if (a == 0):
x = 0
y = 1
return b
# To store results of recursive call
gcd = gcdExtended(b % a, a)
x1 = x
y1 = y
# Update x and y using results of recursive
# call
x = y1 - int(b / a) * x1
y = x1
return gcd
def modInverse(a, m):
g = gcdExtended(a, m)
# Return -1 if b and m are not co-prime
if (g != 1):
return -1
# m is added to handle negative x
return (x % m + m) % m
# Function to compute a/b under modulo m
def modDivide(a, b, m):
a = a % m
inv = modInverse(b, m)
if (inv == -1):
return 0
else:
return (inv * a) % m
# Function to calculate nCr % p
def nCr(n, r, p):
# Edge Case which is not possible
if (r > n):
return 0
# Optimization for the cases when r is large
if (r > n - r):
r = n - r
# x stores the current result at
x = 1
# each iteration
# Initialized to 1 as nC0 is always 1.
for i in range(1, r + 1):
# Formula derived for calculating result is
# C(n,r-1)*(n-r+1)/r
# Function calculates x*(n-i+1) % p.
x = moduloMultiplication(x, (n + 1 - i), p)
# Function calculates x/i % p.
x = modDivide(x, i, p)
return x
# Driver Code
n = 5
r = 3
p = 1000000007
print("Value of nCr % p is ", nCr(n, r, p))
# This code is contributed by phasing17
C#
// C# program to find the nCr%p
// based on optimal Dynamic
// Programming implementation and
// Pascal Triangle concepts
using System;
using System.Collections.Generic;
class GFG
{
// Returns (a * b) % mod
static long moduloMultiplication(long a, long b, long mod)
{
// Initialize result
long res = 0;
// Update a if it is more than
// or equal to mod
a %= mod;
while (b > 0) {
// If b is odd, add a with result
if ((b & 1) != 0)
res = (res + a) % mod;
// Here we assume that doing 2*a
// doesn't cause overflow
a = (2 * a) % mod;
b >>= 1; // b = b / 2
}
return res;
}
// Global Variables
static long x, y;
// Function for extended Euclidean Algorithm
static long gcdExtended(long a, long b){
// Base Case
if (a == 0)
{
x = 0;
y = 1;
return b;
}
// To store results of recursive call
long gcd = gcdExtended(b % a, a);
long x1 = x;
long y1 = y;
// Update x and y using results of recursive
// call
x = y1 - (b / a) * x1;
y = x1;
return gcd;
}
static long modInverse(long a, long m)
{
long g = gcdExtended(a, m);
// Return -1 if b and m are not co-prime
if (g != 1)
return -1;
// m is added to handle negative x
return (x % m + m) % m;
}
// Function to compute a/b under modulo m
static long modDivide(long a, long b, long m)
{
a = a % m;
long inv = modInverse(b, m);
if (inv == -1)
return 0;
else
return (inv * a) % m;
}
// Function to calculate nCr % p
static long nCr(long n, long r, long p)
{
// Edge Case which is not possible
if (r > n)
return 0;
// Optimization for the cases when r is large
if (r > n - r)
r = n - r;
// x stores the current result at
long x = 1;
// each iteration
// Initialized to 1 as nC0 is always 1.
for (long i = 1L; i <= r; i++) {
// Formula derived for calculating result is
// C(n,r-1)*(n-r+1)/r
// Function calculates x*(n-i+1) % p.
x = moduloMultiplication(x, (n + 1L - i), p);
// Function calculates x/i % p.
x = modDivide(x, i, p);
}
return x;
}
// Driver Code
public static void Main(string[] args)
{
long n = 5, r = 3, p = 1000000007;
Console.Write("Value of nCr % p is " + nCr(n, r, p));
}
}
// This code is contributed by phasing17
Javascript
// JavaScript program to find the nCr%p
// based on optimal Dynamic
// Programming implementation and
// Pascal Triangle concepts
// Returns (a * b) % mod
function moduloMultiplication(a, b, mod)
{
// Initialize result
let res = 0;
// Update a if it is more than
// or equal to mod
a %= mod;
while (b) {
// If b is odd, add a with result
if (b & 1)
res = (res + a) % mod;
// Here we assume that doing 2*a
// doesn't cause overflow
a = (2 * a) % mod;
b >>= 1; // b = b / 2
}
return res;
}
// Global Variables
let x, y;
// Function for extended Euclidean Algorithm
function gcdExtended(a, b){
// Base Case
if (a == 0)
{
x = 0;
y = 1;
return b;
}
// To store results of recursive call
let gcd = gcdExtended(b % a, a);
let x1 = x;
let y1 = y;
// Update x and y using results of recursive
// call
x = y1 - Math.floor(b / a) * x1;
y = x1;
return gcd;
}
function modInverse(a, m)
{
let g = gcdExtended(a, m);
// Return -1 if b and m are not co-prime
if (g != 1)
return -1;
// m is added to handle negative x
return (x % m + m) % m;
}
// Function to compute a/b under modulo m
function modDivide(a, b, m)
{
a = a % m;
let inv = modInverse(b, m);
if (inv == -1)
return 0;
else
return (inv * a) % m;
}
// Function to calculate nCr % p
function nCr(n, r, p)
{
// Edge Case which is not possible
if (r > n)
return 0;
// Optimization for the cases when r is large
if (r > n - r)
r = n - r;
// x stores the current result at
let x = 1;
// each iteration
// Initialized to 1 as nC0 is always 1.
for (var i = 1; i <= r; i++) {
// Formula derived for calculating result is
// C(n,r-1)*(n-r+1)/r
// Function calculates x*(n-i+1) % p.
x = moduloMultiplication(x, (n + 1 - i), p);
// Function calculates x/i % p.
x = modDivide(x, i, p);
}
return x;
}
// Driver Code
let n = 5, r = 3, p = 1000000007;
console.log("Value of nCr % p is ", nCr(n, r, p));
// This code is contributed by phasing17
Value of nCr % p is 10
Análisis de Complejidad:
- El código anterior necesita un espacio adicional de O(1) para los cálculos.
- El tiempo involucrado en el cálculo de nCr % p es del orden O(n).
Este artículo ha sido mejorado por Aryan Gupta . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA