¿Cómo implementar un descenso de gradiente en Python para encontrar un mínimo local?

Descenso de gradientees un algoritmo iterativo que se utiliza para minimizar una función encontrando los parámetros óptimos. El descenso de gradiente se puede aplicar a cualquier función de dimensión, es decir, 1-D, 2-D, 3-D. En este artículo, trabajaremos para encontrar mínimos globales para la función parabólica (2-D) e implementaremos el descenso de gradiente en Python para encontrar los parámetros óptimos para la ecuación de regresión lineal (1-D). Antes de sumergirnos en la parte de implementación, asegurémonos del conjunto de parámetros necesarios para implementar el algoritmo de descenso de gradiente. Para implementar un algoritmo de descenso de gradiente, necesitamos una función de costo que debe minimizarse, el número de iteraciones, una tasa de aprendizaje para determinar el tamaño del paso en cada iteración mientras se avanza hacia el mínimo, derivadas parciales de peso y sesgo para actualizar los parámetros. en cada iteración, y una función de predicción. 

Hasta ahora hemos visto los parámetros necesarios para el descenso de gradiente. Ahora mapeemos los parámetros con el algoritmo de descenso de gradiente y trabajemos en un ejemplo para comprender mejor el descenso de gradiente. Consideremos una ecuación parabólica y=4x ² . Al observar la ecuación, podemos identificar que la función parabólica es mínima en x = 0, es decir, en x=0, y=0. Por lo tanto x=0 es el mínimo local de la función parabólica y=4x ² . Ahora veamos el algoritmo para el descenso de gradiente y cómo podemos obtener los mínimos locales aplicando el descenso de gradiente:

Algoritmo para descenso de gradiente

Los pasos deben hacerse en proporción al negativo de la función gradiente (alejarse del gradiente) en el punto actual para encontrar los mínimos locales. Ascenso de gradiente es el procedimiento para acercarse a un máximo local de una función dando pasos proporcionales al positivo del gradiente (moviéndose hacia el gradiente).

repeat until convergence
{
    w = w - (learning_rate * (dJ/dw))
    b = b - (learning_rate * (dJ/db))
}

Paso 1: Inicializar todos los parámetros necesarios y derivar la función de gradiente para la ecuación parabólica 4x ² . La derivada de x ² es 2x, por lo que la derivada de la ecuación parabólica 4x ² será 8x. 

x ₀ = 3 (inicialización aleatoria de x)

learning_rate = 0.01 (para determinar el tamaño del paso mientras se avanza hacia los mínimos locales)

gradiente =   (Cálculo de la función de gradiente)

Paso 2: Realicemos 3 iteraciones de descenso de gradiente:

Para cada iteración, continúe actualizando el valor de x en función de la fórmula de descenso de gradiente.

Iteration 1:
    x1 = x0 - (learning_rate * gradient)
    x1 = 3 - (0.01 * (8 * 3))
    x1 = 3 - 0.24
    x1 = 2.76

Iteration 2:
    x2 = x1 - (learning_rate * gradient)
    x2 = 2.76 - (0.01 * (8 * 2.76))
    x2 = 2.76 - 0.2208
    x2 = 2.5392

Iteration 3:
    x3 = x2 - (learning_rate * gradient)
    x3 = 2.5392 - (0.01 * (8 * 2.5392))
    x3 = 2.5392 - 0.203136
    x3 = 2.3360

De las tres iteraciones anteriores de descenso de gradiente, podemos notar que el valor de x está disminuyendo iteración por iteración y convergerá lentamente a 0 (mínimos locales) al ejecutar el descenso de gradiente para más iteraciones. Ahora puede tener una pregunta, ¿para cuántas iteraciones deberíamos ejecutar el descenso de gradiente?

Podemos establecer un umbral de parada, es decir, cuando la diferencia entre el valor anterior y el actual de x se vuelve menor que el umbral de parada, detenemos las iteraciones. Cuando se trata de la implementación de descenso de gradiente para algoritmos de aprendizaje automático y algoritmos de aprendizaje profundo, tratamos de minimizar la función de costo en los algoritmos que usan descenso de gradiente. Ahora que tenemos claro el funcionamiento interno del descenso de gradiente, echemos un vistazo a la implementación de Python del descenso de gradiente donde minimizaremos la función de costo del algoritmo de regresión lineal y encontraremos la línea de mejor ajuste. En nuestro caso los parámetros se mencionan a continuación:

Función de predicción

La función de predicción del algoritmo de regresión lineal es una ecuación lineal dada por y=wx+b. 

prediction_function (y) = (w * x) + b
Here, x is the independent variable
      y is the dependent variable
      w is the weight associated with input variable
      b is the bias

función de costo

La función de costo se utiliza para calcular la pérdida en función de las predicciones realizadas. En la regresión lineal, usamos el error cuadrático medio para calcular la pérdida. El error cuadrático medio es la suma de las diferencias al cuadrado entre los valores reales y predichos.

Función de Costo (J) = 

Aquí, n es el número de muestras

Derivadas Parciales (Gradientes)

Cálculo de las derivadas parciales de peso y sesgo mediante la función de coste. Obtenemos:

Actualización de parámetros

Actualización del peso y sesgo restando la multiplicación de las tasas de aprendizaje y sus respectivos gradientes.

w = w - (learning_rate * (dJ/dw))
b = b - (learning_rate * (dJ/db))

Implementación de Python para descenso de gradiente

En la parte de implementación, escribiremos dos funciones, una será la función de costo que toma la salida real y la salida pronosticada como entrada y devuelve la pérdida, la segunda será la función de descenso de gradiente real que toma la variable independiente, objetivo variable como entrada y encuentra la mejor línea de ajuste utilizando el algoritmo de descenso de gradiente. Las iteraciones, la tasa de aprendizaje y el umbral de parada son los parámetros de ajuste para el algoritmo de descenso de gradiente y el usuario puede ajustarlos. En la función principal, inicializaremos datos aleatorios relacionados linealmente y aplicaremos el algoritmo de descenso de gradiente en los datos para encontrar la mejor línea de ajuste. El peso y el sesgo óptimos encontrados mediante el algoritmo de descenso de gradiente se utilizan posteriormente para trazar la línea de mejor ajuste en la función principal.

# Importing Libraries
import numpy as np
import matplotlib.pyplot as plt
 
def mean_squared_error(y_true, y_predicted):
     
    # Calculating the loss or cost
    cost = np.sum((y_true-y_predicted)**2) / len(y_true)
    return cost
 
# Gradient Descent Function
# Here iterations, learning_rate, stopping_threshold
# are hyperparameters that can be tuned
def gradient_descent(x, y, iterations = 1000, learning_rate = 0.0001,
                     stopping_threshold = 1e-6):
     
    # Initializing weight, bias, learning rate and iterations
    current_weight = 0.1
    current_bias = 0.01
    iterations = iterations
    learning_rate = learning_rate
    n = float(len(x))
     
    costs = []
    weights = []
    previous_cost = None
     
    # Estimation of optimal parameters
    for i in range(iterations):
         
        # Making predictions
        y_predicted = (current_weight * x) + current_bias
         
        # Calculationg the current cost
        current_cost = mean_squared_error(y, y_predicted)
 
        # If the change in cost is less than or equal to
        # stopping_threshold we stop the gradient descent
        if previous_cost and abs(previous_cost-current_cost)<=stopping_threshold:
            break
         
        previous_cost = current_cost
 
        costs.append(current_cost)
        weights.append(current_weight)
         
        # Calculating the gradients
        weight_derivative = -(2/n) * sum(x * (y-y_predicted))
        bias_derivative = -(2/n) * sum(y-y_predicted)
         
        # Updating weights and bias
        current_weight = current_weight - (learning_rate * weight_derivative)
        current_bias = current_bias - (learning_rate * bias_derivative)
                 
        # Printing the parameters for each 1000th iteration
        print(f"Iteration {i+1}: Cost {current_cost}, Weight \
        {current_weight}, Bias {current_bias}")
     
     
    # Visualizing the weights and cost at for all iterations
    plt.figure(figsize = (8,6))
    plt.plot(weights, costs)
    plt.scatter(weights, costs, marker='o', color='red')
    plt.title("Cost vs Weights")
    plt.ylabel("Cost")
    plt.xlabel("Weight")
    plt.show()
     
    return current_weight, current_bias
 
 
def main():
     
    # Data
    X = np.array([32.50234527, 53.42680403, 61.53035803, 47.47563963, 59.81320787,
           55.14218841, 52.21179669, 39.29956669, 48.10504169, 52.55001444,
           45.41973014, 54.35163488, 44.1640495 , 58.16847072, 56.72720806,
           48.95588857, 44.68719623, 60.29732685, 45.61864377, 38.81681754])
    Y = np.array([31.70700585, 68.77759598, 62.5623823 , 71.54663223, 87.23092513,
           78.21151827, 79.64197305, 59.17148932, 75.3312423 , 71.30087989,
           55.16567715, 82.47884676, 62.00892325, 75.39287043, 81.43619216,
           60.72360244, 82.89250373, 97.37989686, 48.84715332, 56.87721319])
 
    # Estimating weight and bias using gradient descent
    estimated_weight, eatimated_bias = gradient_descent(X, Y, iterations=2000)
    print(f"Estimated Weight: {estimated_weight}\nEstimated Bias: {eatimated_bias}")
 
    # Making predictions using estimated parameters
    Y_pred = estimated_weight*X + eatimated_bias
 
    # Plotting the regression line
    plt.figure(figsize = (8,6))
    plt.scatter(X, Y, marker='o', color='red')
    plt.plot([min(X), max(X)], [min(Y_pred), max(Y_pred)], color='blue',markerfacecolor='red',
             markersize=10,linestyle='dashed')
    plt.xlabel("X")
    plt.ylabel("Y")
    plt.show()
 
     
if __name__=="__main__":
    main()

Producción:

Iteración 1: Costo 4352.088931274409, Peso 0.7593291142562117, Sesgo 0.02288558130709

Iteración 2: Costo 1114.8561474350017, Peso 1.081602958862324, Sesgo 0.02918014748569513  

Iteración 3: Costo 341.42912086804455, Peso 1.2391274084945083, Sesgo 0.03225308846928192 

Iteración 4: Costo 156.64495290904443, Peso 1.3161239281746984, Sesgo 0.03375132986012604 

Iteración 5: Costo 112.49704004742098, Peso 1.3537591652024805, Sesgo 0.034479873154934775

Iteración 6: Costo 101.9493925395456, Peso 1.3721549833978113, Sesgo 0.034832195392868505 

Iteración 7: Costo 99.4293893333546, Peso 1.3811467575154601, Sesgo 0.03500062439068245   

Iteración 8: Costo 98.82731958262897, Peso 1.3855419247507244, Sesgo 0.03507916814736111  

Iteración 9: Costo 98.68347500997261, Peso 1.3876903144657764, Sesgo 0.035113776874486774 

Iteración 10: Costo 98.64910780902792, Peso 1.3887405007983562, Sesgo 0.035126910596389935

Iteración 11: Costo 98.64089651459352, Peso 1.389253895811451, Sesgo 0.03512954755833985  

Iteración 12: Costo 98.63893428729509, Peso 1.38950491235671, Sesgo 0.035127053821718185  

Iteración 13: Costo 98.63846506273883, Peso 1.3896276808137857, Sesgo 0.035122052266051224

Iteración 14: Costo 98.63835254057648, Peso 1.38968776283053, Sesgo 0.03511582492978764   

Iteración 15: Costo 98.63832524036214, Peso 1.3897172043139192, Sesgo 0.03510899846107016 

Iteración 16: Costo 98.63831830104695, Peso 1.389731668997059, Sesgo 0.035101879159522745 

Iteración 17: Costo 98.63831622628217, Peso 1.389738813163012, Sesgo 0.03509461674147458  

Peso estimado: 1.389738813163012

Sesgo estimado: 0.03509461674147458

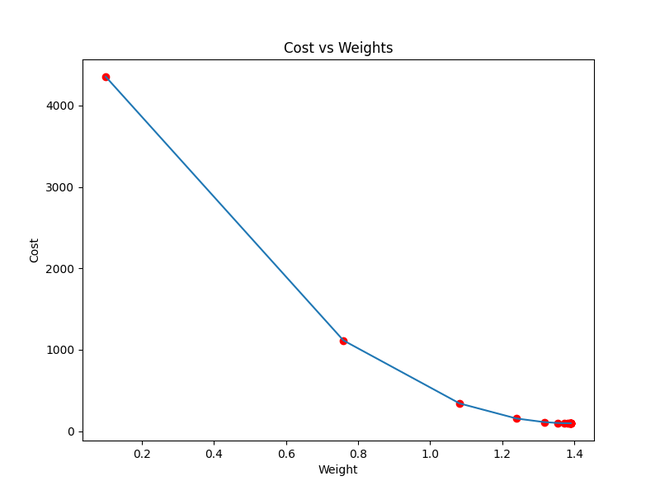
Función de costo que se aproxima a los mínimos locales

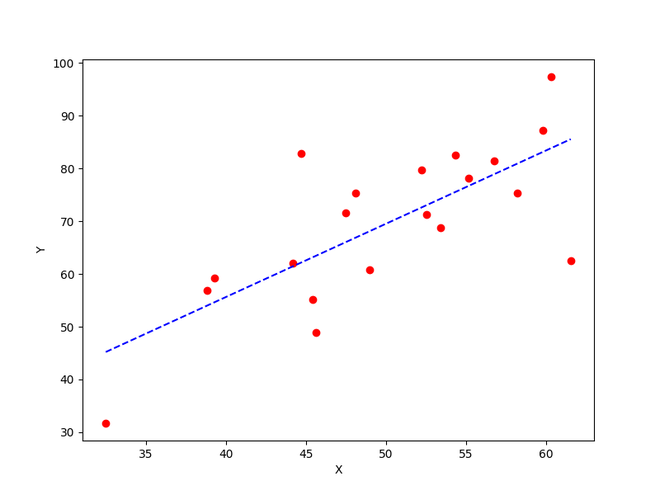
La mejor línea de ajuste obtenida usando gradiente descendente