LOESS o LOWESS son métodos de regresión no paramétricos que combinan múltiples modelos de regresión en un metamodelo basado en el vecino más cercano. LOESS combina gran parte de la simplicidad de la regresión lineal de mínimos cuadrados con la flexibilidad de la regresión no lineal. Lo hace ajustando modelos simples a subconjuntos localizados de los datos para construir una función que describa la variación en los datos, punto por punto.
- Este algoritmo se usa para hacer predicciones cuando existe una relación no lineal entre las características.
- La regresión lineal ponderada localmente es un algoritmo de aprendizaje supervisado.
- Es un algoritmo no paramétrico.
- doneNo existe ninguna fase de entrenamiento. Todo el trabajo se realiza durante la fase de prueba/mientras se hacen predicciones.
Supongamos que queremos evaluar la función de hipótesis h en un determinado punto de consulta x. Para la regresión lineal, haríamos lo siguiente: ![]()
![]()
Para la regresión lineal ponderada localmente, haremos lo siguiente: ![]()
![]()
donde w(i) es a es un «peso» no negativo asociado con el punto de entrenamiento x(i). Se da una mayor «preferencia» a los puntos en el conjunto de entrenamiento que se encuentran en la vecindad de x que a los puntos que se encuentran lejos de x. entonces, para x(i) que se encuentra más cerca del punto de consulta x, el valor de w(i) es grande, mientras que para x(i) que se encuentra lejos de x, el valor de w(i) es pequeño.
w(i) se puede elegir como – 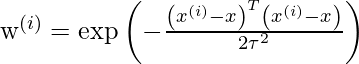
Directamente usando una solución de formulario cerrado para encontrar parámetros- ![]()
Código: Importación de bibliotecas:
python
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
plt.style.use("seaborn")
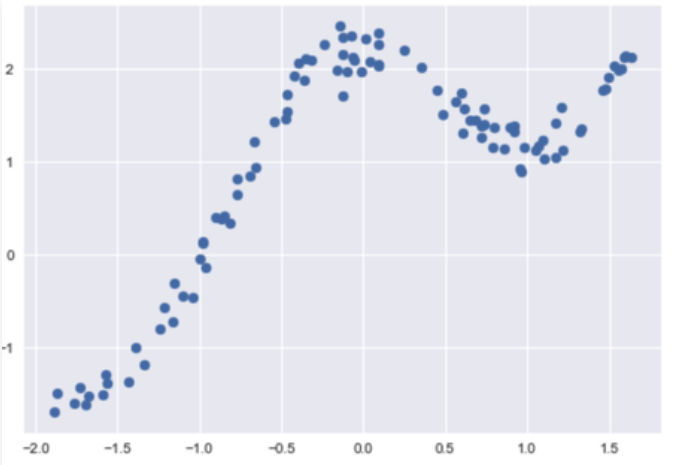
Código: Cargando datos:
python
# Loading CSV files from local storage
dfx = pd.read_csv('weightedX_LOWES.csv')
dfy = pd.read_csv('weightedY_LOWES.csv')
# Getting data from DataFrame Object and storing in numpy n-dim arrays
X = dfx.values
Y = dfy.values
Producción:
Código: Función para calcular la array de peso:
python
# function to calculate W weight diagonal Matrix used in calculation of predictions def get_WeightMatrix_for_LOWES(query_point, Training_examples, Bandwidth): # M is the No of training examples M = Training_examples.shape[0] # Initialising W with identity matrix W = np.mat(np.eye(M)) # calculating weights for query points for i in range(M): xi = Training_examples[i] denominator = (-2 * Bandwidth * Bandwidth) W[i, i] = np.exp(np.dot((xi-query_point), (xi-query_point).T)/denominator) return W
Código: Hacer predicciones:
python
# function to make predictions def predict(training_examples, Y, query_x, Bandwidth): M = Training_examples.shape[0] all_ones = np.ones((M, 1)) X_ = np.hstack((training_examples, all_ones)) qx = np.mat([query_x, 1]) W = get_WeightMatrix_for_LOWES(qx, X_, Bandwidth) # calculating parameter theta theta = np.linalg.pinv(X_.T*(W * X_))*(X_.T*(W * Y)) # calculating predictions pred = np.dot(qx, theta) return theta, pred
Código: Visualizar predicciones:
python
# visualise predicted values with respect
# to original target values
Bandwidth = 0.1
X_test = np.linspace(-2, 2, 20)
Y_test = []
for query in X_test:
theta, pred = predict(X, Y, query, Bandwidth)
Y_test.append(pred[0][0])
horizontal_axis = np.array(X)
vertical_axis = np.array(Y)
plt.title("Tau / Bandwidth Param %.2f"% Bandwidth)
plt.scatter(horizontal_axis, vertical_axis)
Y_test = np.array(Y_test)
plt.scatter(X_test, Y_test, color ='red')
plt.show()
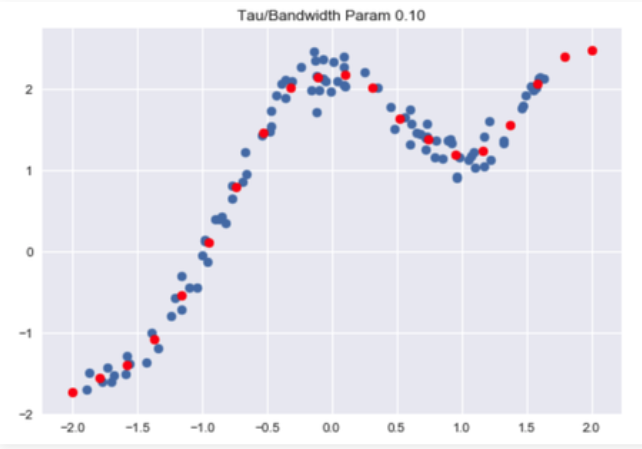
Publicación traducida automáticamente
Artículo escrito por harshitmuhal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA