Diferencia entre el descenso de gradiente por lotes y el descenso de gradiente estocástico

Para entrenar un modelo de regresión lineal, tenemos que aprender algunos parámetros del modelo, como pesos de características y términos de sesgo. Un enfoque para hacer lo mismo es Gradient Descent, que es un algoritmo de optimización iterativo capaz de ajustar los parámetros del modelo minimizando la función de costo sobre los datos del tren. Es un algoritmo completo, es decir, se garantiza encontrar el mínimo global (solución óptima) dado que hay suficiente tiempo y la tasa de aprendizaje no es muy alta. Dos variantes importantes de descenso de gradiente que se utilizan ampliamente en la regresión lineal, así como en las redes neuronales, son el descenso de gradiente por lotes y el descenso de gradiente estocástico (SGD).

Descenso de gradiente por lotes: el descenso de gradiente por lotes implica cálculos sobre el conjunto de entrenamiento completo en cada paso, por lo que es muy lento en datos de entrenamiento muy grandes. Por lo tanto, se vuelve muy costoso computacionalmente hacer Batch GD. Sin embargo, esto es excelente para variedades de error convexas o relativamente suaves. Además, Batch GD escala bien con la cantidad de características.

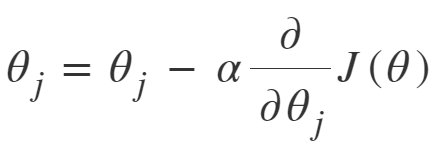
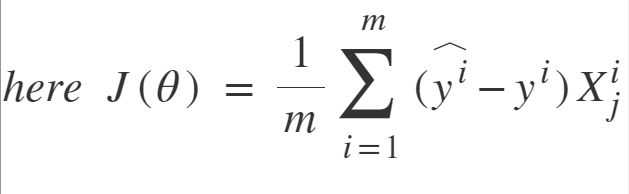
Descenso de gradiente estocástico: SGD intenta resolver el problema principal en el descenso de gradiente por lotes, que es el uso de datos de entrenamiento completos para calcular gradientes en cada paso. SGD es de naturaleza estocástica, es decir, recoge una instancia «aleatoria» de datos de entrenamiento en cada paso y luego calcula el gradiente haciéndolo mucho más rápido ya que hay muchos menos datos para manipular en un solo momento, a diferencia de Batch GD.

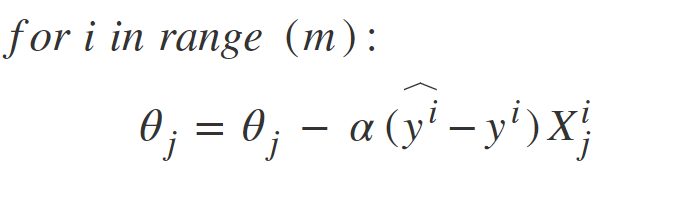
Hay una desventaja de la naturaleza estocástica de SGD, es decir, una vez que se acerca al valor mínimo, no se estabiliza, sino que rebota, lo que nos da un buen valor para los parámetros del modelo, pero no el óptimo, lo que se puede resolver reduciendo el aprendizaje. tasa en cada paso que puede reducir el rebote y SGD podría establecerse en un mínimo global después de un tiempo.

Diferencia entre el descenso de gradiente por lotes y el descenso de gradiente estocástico

S. NO.	Descenso de gradiente por lotes	Descenso de gradiente estocástico
1.	Calcula el gradiente utilizando toda la muestra de entrenamiento	Calcula el gradiente usando una sola muestra de entrenamiento
2.	Algoritmo lento y computacionalmente costoso	Más rápido y menos costoso computacionalmente que Batch GD
3.	No recomendado para grandes muestras de formación.	Se puede usar para muestras de entrenamiento grandes.
4.	De naturaleza determinista.	De naturaleza estocástica.
5.	Da una solución óptima dado el tiempo suficiente para converger.	Da una buena solución pero no óptima.
6.	No se requiere barajar aleatoriamente los puntos.	La muestra de datos debe estar en un orden aleatorio, y es por eso que queremos barajar el conjunto de entrenamiento para cada época.
7.	No se puede escapar fácilmente de los mínimos locales poco profundos.	SGD puede escapar de los mínimos locales poco profundos más fácilmente.
8.	La convergencia es lenta.	Alcanza la convergencia mucho más rápido.