Programa para convertir coordenadas polares a coordenadas cartesianas equivalentes

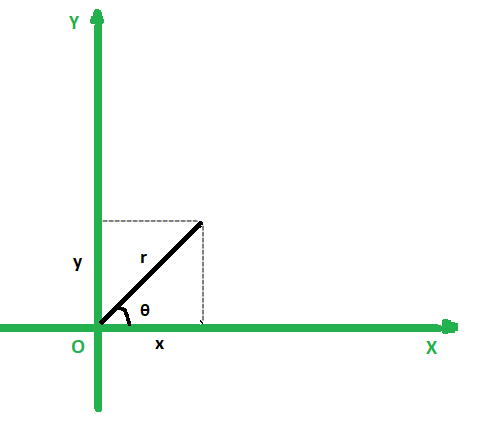
Dados dos números enteros r y θ (en grados) que representan las coordenadas polares de un punto (r, θ) , la tarea es encontrar las coordenadas cartesianas del punto dado.

Ejemplos:

Entrada: r = 1,4142, θ = 45
Salida: 1,000, 1,000

Entrada: r = 3, θ = 30
Salida: 2.598, 1.500

Aproximación: Sean las coordenadas cartesianas del punto (x, y). Las coordenadas polares y las coordenadas cartesianas se pueden relacionar mediante las siguientes ecuaciones:

x = r*cosθ y y = r*sinθ

Siga los pasos a continuación para resolver el problema:

• Convierta θ de grados a radianes como θ(en radianes) = θ (en grados) * (3.14159 / 180) .
• Almacene las coordenadas x e y en una variable X e Y respectivamente.
• Aplique la fórmula de transformación y actualice el valor de X = r * cosθ e Y = r * sinθ .
• Imprime el valor de X e Y como resultado.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to convert degree to radian
double ConvertDegToRad(double degree)
{
    double pi = 3.14159;
    return (degree * (pi / 180.0));
}
 
// Function to convert the polar
// coordinate to cartesian
void ConvertToCartesian(
    pair<double, double> polar)
{
 
    // Convert degrees to radian
    polar.second = ConvertDegToRad(
        polar.second);
 
    // Applying the formula:
    // x = rcos(theta), y = rsin(theta)
    pair<double, double> cartesian
        = { polar.first * cos(polar.second),
            polar.first * sin(polar.second) };
 
    // Print cartesian coordinates
    printf("%0.3f, %0.3f",
           cartesian.first,
           cartesian.second);
}
 
// Driver Code
int main()
{
    // Given polar coordinates
    pair<double,
         double>
        polar = { 1.4142, 45 };
 
    // Function to convert polar
    // coordinates to equivalent
    // cartesian coordinates
    ConvertToCartesian(polar);
 
    return 0;
}

// Java code of above approach
import java.util.*;
 
class GFG
{
 
  // Function to convert degree to radian
  static double ConvertDegToRad(double degree)
  {
    double pi = 3.14159;
    return (degree * (pi / 180.0));
  }
 
  // Function to convert the polar
  // coordinate to cartesian
  static void ConvertToCartesian(
    double[] polar)
  {
 
    // Convert degrees to radian
    polar[1] = ConvertDegToRad(
      polar[1]);
 
    // Applying the formula:
    // x = rcos(theta), y = rsin(theta)
    double[] cartesian
      = { polar[0] * Math.cos(polar[1]),
         polar[0] * Math.sin(polar[1]) };
 
    // Print cartesian coordinates
    System.out.print(String.format("%.3f", cartesian[0])+" "+String.format("%.3f", cartesian[1]));
 
  }
 
  // Driver code
  public static void main(String[] args)
  {
    // Given polar coordinates
 
    double[] polar = { 1.4142, 45 };
 
    // Function to convert polar
    // coordinates to equivalent
    // cartesian coordinates
    ConvertToCartesian(polar);
 
  }
}
 
// This code is contributed by offbeat

# Python 3 program for the above approach
import math
 
# Function to convert degree to radian
def ConvertDegToRad(degree):
    pi = 3.14159
    return (degree * (pi / 180.0))
 
# Function to convert the polar
# coordinate to cartesian
def ConvertToCartesian(polar):
 
    # Convert degrees to radian
    polar[1] = ConvertDegToRad(polar[1])
 
    # Applying the formula:
    # x = rcos(theta), y = rsin(theta)
    cartesian = [polar[0] * math.cos(polar[1]),
                 polar[0] * math.sin(polar[1])]
 
    # Print cartesian coordinates
    print('%.3f' % cartesian[0],
          '%.3f' % cartesian[1])
 
# Driver Code
if __name__ == "__main__":
 
    # Given polar coordinates
    polar = [1.4142, 45]
 
    # Function to convert polar
    # coordinates to equivalent
    # cartesian coordinates
    ConvertToCartesian(polar)
 
    # This code is contributed by chitranayal.

// C# program for the above approach
using System;
 
class GFG
{
 
  // Function to convert degree to radian
  static Double ConvertDegToRad(Double degree)
  {
    Double pi = 3.14159;
    return (degree * (pi / 180.0));
  }
 
  // Function to convert the polar
  // coordinate to cartesian
  static void ConvertToCartesian(
    Double[] polar)
  {
 
    // Convert degrees to radian
    polar[1] = ConvertDegToRad(
      polar[1]);
 
    // Applying the formula:
    // x = rCos(theta), y = rSin(theta)
    Double[] cartesian
      = { polar[0] * Math.Cos(polar[1]),
         polar[0] * Math.Sin(polar[1]) };
 
    // Print cartesian coordinates
    Console.Write(String.Format("{0:0.000}", cartesian[0])+
                  ", "+String.Format("{0:0.000}", cartesian[1]));
 
  }
 
  // Driver code
  public static void Main()
  {
 
    // Given polar coordinates
    Double[] polar = { 1.4142, 45 };
 
    // Function to convert polar
    // coordinates to equivalent
    // cartesian coordinates
    ConvertToCartesian(polar);
 
  }
}
 
// This code is contributed by Shubham Singh

<script>
 
// JavaScript code of above approach
 
// Function to convert degree to radian
function ConvertDegToRad(degree)
{
    let pi = 3.14159;
    return (degree * (pi / 180.0));
}
 
// Function to convert the polar
  // coordinate to cartesian
function ConvertToCartesian(polar)
{
    // Convert degrees to radian
    polar[1] = ConvertDegToRad(
      polar[1]);
  
    // Applying the formula:
    // x = rcos(theta), y = rsin(theta)
    let cartesian
      = [ polar[0] * Math.cos(polar[1]),
         polar[0] * Math.sin(polar[1]) ];
  
    // Print cartesian coordinates
    document.write((cartesian[0]).toFixed(3)+", "
    +(cartesian[1]).toFixed(3));
}
 
// Driver code
let polar=[1.4142, 45 ];
// Function to convert polar
// coordinates to equivalent
// cartesian coordinates
ConvertToCartesian(polar);
 
// This code is contributed by avanitrachhadiya2155
 
</script>

1.000, 1.000

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)