Regresión lineal:
Es el tipo básico y comúnmente utilizado para el análisis predictivo. Es un enfoque estadístico para modelar la relación entre una variable dependiente y un conjunto dado de variables independientes.
Estos son de dos tipos:
- Regresión lineal simple
- Regresión lineal múltiple
Analicemos la regresión lineal múltiple usando Python.
La regresión lineal múltiple intenta modelar la relación entre dos o más características y una respuesta ajustando una ecuación lineal a los datos observados. Los pasos para realizar una regresión lineal múltiple son casi similares a los de una regresión lineal simple. La diferencia radica en la evaluación. Podemos usarlo para averiguar qué factor tiene el mayor impacto en el resultado previsto y ahora las diferentes variables se relacionan entre sí.
Aquí: Y = b0 + b1 * x1 + b2 * x2 + b3 * x3 + …… bn * xn
Y = variable dependiente y x1, x2, x3, …… xn = múltiples variables independientes
Asunción del modelo de regresión:
- Linealidad: La relación entre las variables dependientes e independientes debe ser lineal.
- Homocedasticidad: Debe mantenerse la varianza constante de los errores.
- Normalidad multivariante: la regresión múltiple asume que los residuos se distribuyen normalmente.
- Falta de multicolinealidad: se supone que hay poca o ninguna multicolinealidad en los datos.
Variable ficticia:
Como sabemos, en el modelo de regresión múltiple usamos muchos datos categóricos. El uso de datos categóricos es un buen método para incluir datos no numéricos en el modelo de regresión respectivo. Los datos categóricos se refieren a valores de datos que representan categorías: valores de datos con un número fijo y desordenado de valores, por ejemplo, género (masculino/femenino). En el modelo de regresión, estos valores se pueden representar mediante variables ficticias.
Estas variables consisten en valores como 0 o 1 que representan la presencia y ausencia de valores categóricos.
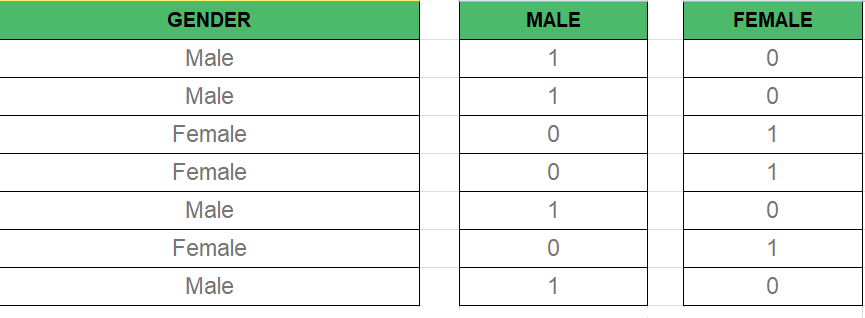
Trampa de variable ficticia:
La trampa de variable ficticia es una condición en la que dos o más están altamente correlacionados. En términos simples, podemos decir que una variable se puede predecir a partir de la predicción de la otra. La solución de la trampa de variable ficticia es descartar una de las variables categóricas. Entonces, si hay m variables ficticias, entonces se usan m-1 variables en el modelo.
D2 = D1-1 Here D2, D1 = Dummy Variables
Método de construcción de modelos:
- Todo dentro
- Eliminación hacia atrás
- Selección de reenvío
- Eliminación bidireccional
- Comparación de puntuaciones
Eliminación hacia atrás:
Paso #1: Seleccione un nivel significativo para comenzar en el modelo.
Paso #2: ajuste el modelo completo con todos los predictores posibles.
Paso #3: Considere el predictor con el valor P más alto. Si P > SL vaya al PASO 4, de lo contrario el modelo está Listo.
Paso #4: Eliminar el predictor.
Paso #5: Ajuste el modelo sin esta variable.
Selección hacia adelante:
Paso #1: Seleccione un nivel de significación para ingresar al modelo (por ejemplo, SL = 0.05)
Paso #2: Ajuste todos los modelos de regresión simple y~ x(n). Seleccione el que tenga el valor P más bajo.
Paso #3: Mantenga esta variable y ajuste todos los modelos posibles con un predictor adicional agregado a los que ya tiene.
Paso #4: Considere el predictor con el valor P más bajo. Si P < SL, vaya al paso 3; de lo contrario, el modelo está listo.
Pasos involucrados en cualquier modelo de regresión lineal múltiple
Paso #1: Preprocesamiento de datos
- Importación de las bibliotecas.
- Importación del conjunto de datos.
- Codificación de los datos categóricos.
- Evitar la trampa de la variable ficticia.
- Dividir el conjunto de datos en conjunto de entrenamiento y conjunto de prueba.
Paso n.º 2: ajuste de la regresión lineal múltiple al conjunto de entrenamiento
Paso n.º 3: predicción de los resultados del conjunto de prueba.
Código 1:
Python3
import numpy as np import matplotlib as mpl from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt def generate_dataset(n): x = [] y = [] random_x1 = np.random.rand() random_x2 = np.random.rand() for i in range(n): x1 = i x2 = i/2 + np.random.rand()*n x.append([1, x1, x2]) y.append(random_x1 * x1 + random_x2 * x2 + 1) return np.array(x), np.array(y) x, y = generate_dataset(200) mpl.rcParams['legend.fontsize'] = 12 fig = plt.figure() ax = fig.gca(projection ='3d') ax.scatter(x[:, 1], x[:, 2], y, label ='y', s = 5) ax.legend() ax.view_init(45, 0) plt.show()
Producción:
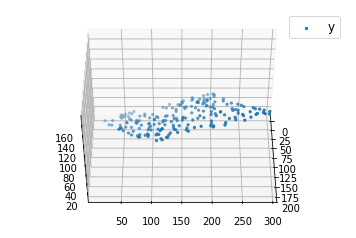
Código 2:
Python3
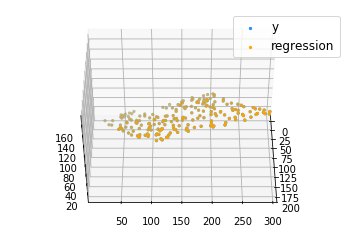
def mse(coef, x, y): return np.mean((np.dot(x, coef) - y)**2)/2 def gradients(coef, x, y): return np.mean(x.transpose()*(np.dot(x, coef) - y), axis = 1) def multilinear_regression(coef, x, y, lr, b1 = 0.9, b2 = 0.999, epsilon = 1e-8): prev_error = 0 m_coef = np.zeros(coef.shape) v_coef = np.zeros(coef.shape) moment_m_coef = np.zeros(coef.shape) moment_v_coef = np.zeros(coef.shape) t = 0 while True: error = mse(coef, x, y) if abs(error - prev_error) <= epsilon: break prev_error = error grad = gradients(coef, x, y) t += 1 m_coef = b1 * m_coef + (1-b1)*grad v_coef = b2 * v_coef + (1-b2)*grad**2 moment_m_coef = m_coef / (1-b1**t) moment_v_coef = v_coef / (1-b2**t) delta = ((lr / moment_v_coef**0.5 + 1e-8) * (b1 * moment_m_coef + (1-b1)*grad/(1-b1**t))) coef = np.subtract(coef, delta) return coef coef = np.array([0, 0, 0]) c = multilinear_regression(coef, x, y, 1e-1) fig = plt.figure() ax = fig.gca(projection ='3d') ax.scatter(x[:, 1], x[:, 2], y, label ='y', s = 5, color ="dodgerblue") ax.scatter(x[:, 1], x[:, 2], c[0] + c[1]*x[:, 1] + c[2]*x[:, 2], label ='regression', s = 5, color ="orange") ax.view_init(45, 0) ax.legend() plt.show()
Producción: