La array de pagos de un juego M * 2 consta de M filas y dos columnas. Este artículo discutirá cómo resolver un juego M * 2 por método gráfico. Además, este artículo discutirá si más de dos líneas se cruzan con el mismo punto en el gráfico, entonces, ¿cómo se puede formar una array de pagos de 2 * 2 ?
Considere el siguiente problema: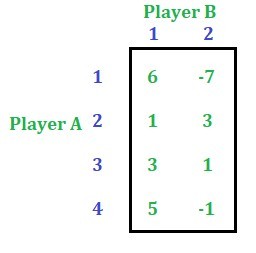
Solución: primero verifique si el problema tiene un punto de silla o no. Este juego no tiene punto de silla.
Paso 1: Reducir el tamaño de la array de pagos del jugador A aplicando la propiedad de dominancia , si existe. El tamaño se está reduciendo solo para simplificar el problema. El juego se puede resolver sin reducir el tamaño también.
En este problema no se aplica la propiedad de dominancia. No podemos simplificar esta array más que esto. Entonces, nos quedamos con el siguiente juego.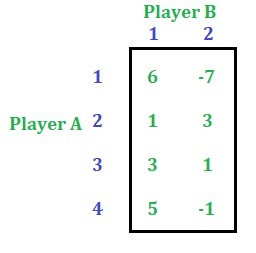
Paso 2: Sea y la probabilidad de selección de la alternativa 1 por parte del jugador B y (1 – y) la probabilidad de selección de la alternativa 2 por parte del jugador B. 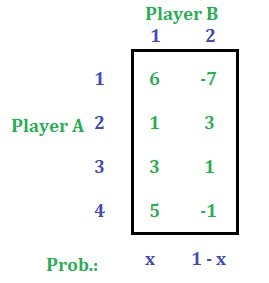
Deduzca la función de ganancia esperada del jugador B con respecto a cada una de las alternativas de jugador A. Ver la tabla a continuación.
Junto con encuentre el valor de la ganancia cuando y = 0 y y = 1 . Ver la tabla a continuación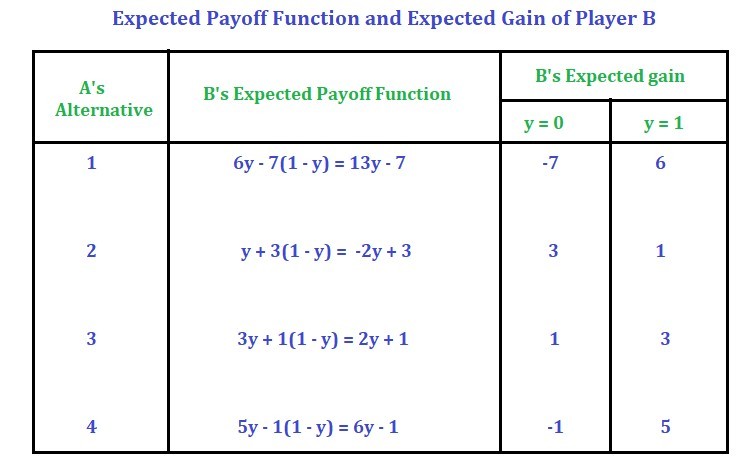
Paso 3: Trace la función de ganancia en un gráfico asumiendo una escala adecuada. Mantenga y en el eje X y la ganancia en el eje Y.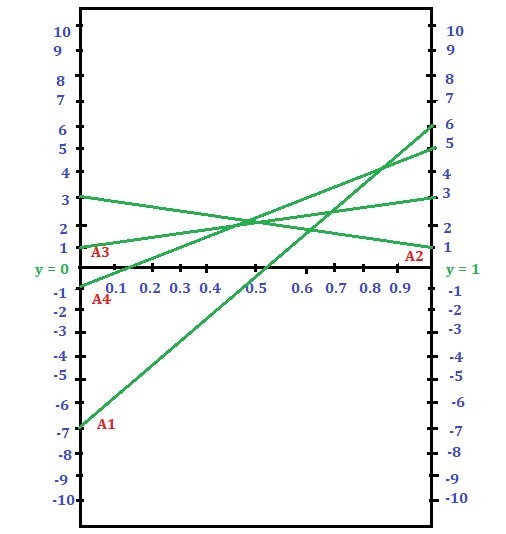
Paso 3: encuentre el punto de intersección más bajo en el límite superior del gráfico –> punto Minimax.
ABCD es el límite superior en el gráfico dado. Hay cuatro puntos de intersección donde B es la intersección más baja. Entonces este punto se llama punto Minimax. 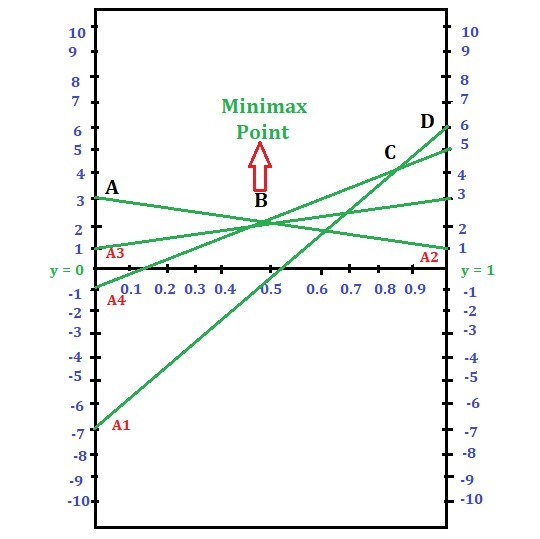
Como hay más de dos líneas que pasan por el punto de intersección más bajo, identificaremos dos líneas con pendientes opuestas que pasen por ese punto. Luego forme una array de pagos de 2 * 2 .
A4, A3 y A2 son tres rectas que pasan por el punto B. Entonces, entre estas tres rectas, A2 y A3 tienen pendientes opuestas, y A2 y A4 tienen pendientes opuestas. Podemos seleccionar cualquiera de los dos pares de líneas. Aquí seleccionamos A2 y A4. Entonces la array de pagos será 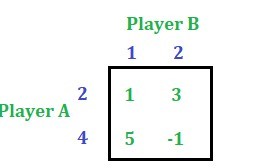
Ahora resuelva el juego anterior segúneste artículo
Después de resolver el juego obtenemos,
Probabilidades de las estrategias del jugador A = [0, 3/4, 0, 1/4]
Probabilidades de las estrategias del jugador B = [1/2, 1/2]
Y el valor del juego es 2
Publicación traducida automáticamente
Artículo escrito por mkumarchaudhary06 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA