Separación de hiperplanos en SVM

Support Vector Machine es el algoritmo de aprendizaje automático supervisado, que se utiliza tanto en la clasificación como en la regresión de modelos. La idea detrás de esto es simplemente encontrar un plano o un límite que separe los datos entre dos clases.

Vectores de apoyo:

Los vectores de soporte son los puntos de datos que están cerca del límite de decisión, son los puntos de datos más difíciles de clasificar, son la clave para que SVM sea una superficie de decisión óptima. El hiperplano óptimo proviene de la clase de función con la capacidad más baja, es decir, el número mínimo de características/parámetros independientes.

Separación de hiperplanos:

A continuación se muestra un ejemplo de un diagrama de dispersión:

En la dispersión anterior, ¿podemos encontrar una línea que pueda separar dos categorías? Tal línea se llama hiperplano de separación. Entonces, ¿por qué se llama hiperplano? Porque en 2 dimensiones es una línea, pero en 1 dimensión puede ser un punto, en 3 dimensiones es un plano y en 3 o más dimensiones es un hiperplano.

Ahora que entendemos el hiperplano, también necesitamos encontrar el hiperplano más optimizado. La idea detrás de que este hiperplano debería estar más alejado de los vectores de soporte. Esta distancia en blanco y negro que separa los hiperplanos y el vector de soporte se conoce como margen. Así, el mejor hiperplano será aquel cuyo margen sea el máximo.

Generalmente, el margen puede tomarse como 2* p, donde p es la distancia b/n que separa el hiperplano y el vector de soporte más cercano. A continuación se muestra el método para calcular el hiperplano linealmente separable.

Un hiperplano separador se puede definir mediante dos términos: un término de intersección denominado b y un vector normal del hiperplano de decisión denominado w. Estos se conocen comúnmente como el vector de peso en el aprendizaje automático. Aquí b se usa para seleccionar el hiperplano, es decir, perpendicular al vector normal. Ahora, dado que todo el plano x en el hiperplano debe satisfacer la siguiente ecuación:

$w^{T} \cdot x = -b$

Ahora, considere el entrenamiento D tal que $\mathbb{D} = \left \{ \left ( \vec{x_i}, y_i \right ) \right \}$ donde $\vec{x_i} \, y_i$ representa el punto de datos n-dimensional y la etiqueta de clase respectivamente. El valor de la etiqueta de clase aquí solo puede ser -1 o +1 (para un problema de 2 clases). El clasificador lineal es entonces:

$f(\vec{x}) = sign(\vec{w^{T}}\vec{x} + b)$

Sin embargo, el margen funcional, por definición de lo anterior, no tiene restricciones, por lo que debemos formular la distancia b/wa del punto de datos x y el límite de decisión. La distancia más corta entre ellos es, por supuesto, la distancia perpendicular, es decir, paralela al vector normal $\vec{w}$ . Un vector unitario en la dirección de este vector normal viene dado por $\frac {\vec{w}}{\left \| \vec{w} \right \|}$ . Ahora,

$\vec{x^{'}}$ can be defined as:

$\vec{x^{'}} = \vec{x} - yr\frac{\vec{w}}{\left \| \vec{w} \right \|}$

Reemplazar x’ por x en la ecuación del clasificador lineal da:

$\vec{w^{T}}\left ( \vec{x} - yr\frac{\vec{w}}{\left \| \vec{w} \right \|}\right ) + b = 0$

Ahora, resolviendo para r da la siguiente ecuación:

$r = y \frac{\vec{w^{T}}\vec{x} + b}{\left \| \vec{w} \right \|}$

donde, r es el margen. Ahora bien, desde la

$\left \| w \right \| = 1$ . The distance equation for a data point to hyperplane for all items in the data could be written as:

$y_i(\vec{w^{T}}\vec{x_i} +b) \geq 1$

o, la ecuación anterior para cada punto de datos:

$r_i = y_i \frac{\vec{w^{T}}\vec{x_i} + b}{\left \| \vec{w} \right \|}$

Aquí, el margen geométrico es:

$\rho = \frac{2}{||\vec{w}||}$

Necesitamos maximizar el margen geométrico tal que:

$\rho =\frac{2}{\left \| \vec{w} \right \|} \forall \left ( \vec{x_i}, y_i \right) \in \mathbb(D); y_i(\vec{w^{T}}\vec{x_i} +b) \geq 1$

Maximizar $\rho$ es lo mismo que minimizar $\frac{1}{\rho} = \frac{||w||}{2}$ , es decir, necesitamos encontrar w y b tales que:

$\frac{1}{2}\vec{w^{T}}\vec{w}$ is minimum $\forall \left ( \vec{x_i}, y_i \right) \in \mathbb{D}; y_i(\vec{w^{T}}\vec{x_i} +b) \geq 1$

Aquí, estamos optimizando una ecuación cuadrática con restricción lineal. Ahora bien, esto nos lleva a encontrar la solución a problemas duales.

Problema de dualidad:

En optimización, el principio de dualidad establece que los problemas de optimización pueden verse desde una perspectiva diferente: el problema primal y el problema dual

$minimize_{x} \, \, f(x) \\ subject \, to \,\, g_i (x) =0 , \,\,\, i= 1,....,p \\ h_i(x) \leq 0 \,\, i= 1,....,m$

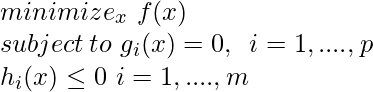
donde, f es la función objetivo g y h son la función de restricción. El problema anterior se puede resolver mediante una técnica como los multiplicadores de Lagrange.

Multiplicadores de Lagrange

El multiplicador de Lagrange es una forma de encontrar mínimos y máximos locales para las funciones con una restricción de igualdad. Los multiplicadores de Lagrange se pueden describir para

En la ecuación de Lagrange:

$\nabla f (x,y) = \nabla \lambda g(x,y) \\ or \\ \nabla f (x,y) - \nabla \lambda g(x,y) =0 \\$

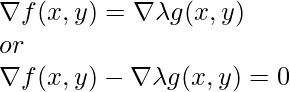
Supongamos que definimos la función tal que

$\nabla L(x,y, \lambda) = \nabla f (x,y) - \nabla \lambda g(x,y)$

La función anterior se conoce como Lagrangiana, ahora, necesitamos encontrar $\nabla L(x,y, \lambda)$ es 0, es decir, el punto donde el gradiente de las funciones f y g son paralelos.

Ejemplo

Considere tener tres puntos con los puntos (1,2) y (2,0) pertenecientes a una clase y (3,2) pertenecientes a otra, geométricamente, podemos observar que la línea de margen máximo será paralela a la línea que conecta los puntos de la dos clases. (1,1) y (2,3) dado un vector de peso como (1,2). La superficie de decisión óptima (hiperplano de separación) se intersecará en (1.5,2). Ahora, podemos calcular el sesgo usando esta conclusión:

$y = x_1 + 2x_2 +b \\ \\ y=0 \\ x_1 =1.5 \\ x_2 =2 \\ \\ 0 = 1.5+ 4 +b \\ \\ b=- 5.5$

.Ahora, la ecuación de la superficie de decisión se convierte en:

$y = x_1 + 2x_2 -5.5$

Ahora, dado que sign $(y_i(w^{T}x_i +b)) \geq 1$ , para minimizar $|\vec{w}|$ , necesitamos verificar la restricción de igualdad o los vectores de soporte. Tomemos w=(a, 2a) por alguna a tal que:

$a + 2a + b = -1 \, for \, point \,(1,1) \\ 2a + 6a + b = 1 \, for \, point \,(2,3) \\$

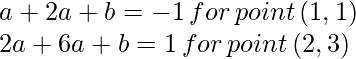
Resolviendo la ecuación anterior se obtiene:

$a =\frac{2}{5}; \, b= \frac{-11}{5}$

esto significa que el margen se convierte en:

$\rho = \frac{2}{||\vec{w}||} \\ = \frac{2}{\sqrt{\frac{4}{25}+ \frac{16}{25}}} \\ = \frac{2}{\frac{2\sqrt{5}}{5}} \\ = \sqrt{5}\\ 2.23$

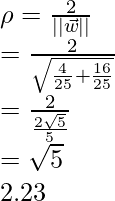
Implementación

En esta implementación, verificaremos el ejemplo anterior utilizando la biblioteca sklearn e intentaremos modelar el ejemplo anterior:

Python3

# Import Necessary libraries/functions
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
 
# define the dataset
X = np.array([[1,1],
             [2,0],
             [2,3]])
Y = np.array([0,0,1])
 
# define support vector classifier with linear kernel
 
clf = SVC(gamma='auto', kernel ='linear')
 
# fit the above data in SVC
clf.fit(X,Y)
 
# plot the decision boundary ,data points,support vector etcv
w = clf.coef_[0]
a = -w[0] / w[1]
 
xx = np.linspace(0,12)
yy = a * xx - clf.intercept_[0] / w[1]
y_neg = a * xx - clf.intercept_[0] / w[1] + 1
y_pos = a * xx - clf.intercept_[0] / w[1] - 1
plt.figure(1,figsize= (15, 10))
plt.plot(xx, yy, 'k',
         label=f"Decision Boundary (y ={w[0]}x1  + {w[1]}x2  {clf.intercept_[0] })")
plt.plot(xx, y_neg, 'b-.',
         label=f"Neg Decision Boundary (-1 ={w[0]}x1  + {w[1]}x2  {clf.intercept_[0] })")
plt.plot(xx, y_pos, 'r-.',
         label=f"Pos Decision Boundary (1 ={w[0]}x1  + {w[1]}x2  {clf.intercept_[0] })")
 
for i in range(3):
  if (Y[i]==0):
      plt.scatter(X[i][0], X[i][1],color='red', marker='o', label='negative')
  else:
      plt.scatter(X[i][0], X[i][1],color='green', marker='x', label='positive')
plt.legend()
plt.show()
 
# calculate margin
print(f'Margin : {2.0 /np.sqrt(np.sum(clf.coef_ ** 2)) }')

Margin : 2.236

Límite de decisión final de SVM

Referencias:

PNL de Stanford

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Problema de dualidad:

Multiplicadores de Lagrange

Implementación

Python3

Referencias:

Deja una respuesta Cancelar la respuesta