LightGBM (máquina potenciadora de gradiente de luz)

LightGBM es un marco de mejora de gradiente basado en árboles de decisión para aumentar la eficiencia del modelo y reducir el uso de memoria. 
Utiliza dos técnicas novedosas: muestreo de un lado basado en gradiente y agrupación de características exclusivas (EFB) , que cumple con las limitaciones del algoritmo basado en histograma que se usa principalmente en todos los marcos GBDT (árbol de decisión de aumento de gradiente). Las dos técnicas de GOSS y EFB que se describen a continuación forman las características del algoritmo LightGBM. Se componen juntos para hacer que el modelo funcione de manera eficiente y proporcionarle una ventaja sobre otros marcos GBDT 
Técnica de muestreo de un lado basada en gradiente para LightGBM: 
Diferentes instancias de datos tienen roles variados en el cálculo de la ganancia de información. Las instancias con gradientes más grandes (es decir, instancias poco entrenadas) contribuirán más a la ganancia de información. GOSS mantiene aquellas instancias con gradientes grandes (p. ej., más grandes que un umbral predefinido, o entre los percentiles superiores) y solo descarta aleatoriamente aquellas instancias con gradientes pequeños para conservar la precisión de la estimación de la ganancia de información. Este tratamiento puede conducir a una estimación de la ganancia más precisa que el muestreo aleatorio uniforme, con la misma tasa de muestreo objetivo, especialmente cuando el valor de la ganancia de información tiene un amplio rango. 
Algoritmo para GOSS: 

Input: I: training data, d: iterations
Input: a: sampling ratio of large gradient data
Input: b: sampling ratio of small gradient data
Input: loss: loss function, L: weak learner
models ? {}, fact ? (1-a)/b
topN ? a × len(I), randN ? b × len(I)
for i = 1 to d do
    preds ? models.predict(I) g ? loss(I, preds), w ? {1, 1, ...}
    sorted ? GetSortedIndices(abs(g))
    topSet ? sorted[1:topN]
    randSet ? RandomPick(sorted[topN:len(I)],
    randN)
    usedSet ? topSet + randSet
    w[randSet] × = fact . Assign weight f act to the
    small gradient data.
    newModel ? L(I[usedSet], g[usedSet],
    w[usedSet])
    models.append(newModel)

Análisis matemático para la técnica GOSS (cálculo de ganancia de varianza en función de división j) 
Para un conjunto de entrenamiento con n instancias {x ₁ , · · ·, x _n }, donde cada x _i es un vector con dimensión s en el espacio X ^s . En cada iteración de aumento de gradiente, los gradientes negativos de la función de pérdida con respecto a la salida del modelo se denotan como {g ₁ , · · ·, g _n }. En este método GOSS, las instancias de entrenamiento se clasifican según los valores absolutos de sus gradientes en orden descendente. Luego, las instancias top-a × 100% con los gradientes más grandes se mantienen y obtenemos un subconjunto de instancias A. Luego, para el conjunto restante A ^cque consta de (1- a) × 100 % de instancias con gradientes más pequeños. Además, muestreamos aleatoriamente un subconjunto B con tamaño b × |A ^c |. Finalmente, dividimos las instancias de acuerdo con la ganancia de varianza estimada en el vector V _j (d) sobre el subconjunto A ? B. 

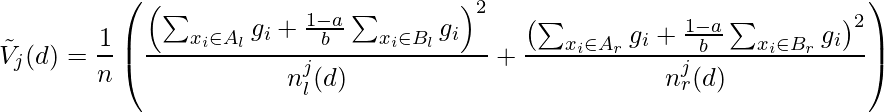
donde A _l = {x _i ? A : x _ij ? d}, A _r = {x _i ? A : x _ij > d}, B _l = {x _i ? B : x _ij ? d}, B _r = {x _i ? B : x _ij > d}, y el coeficiente (1-a)/b se usa para normalizar la suma de los gradientes sobre B de vuelta al tamaño de A ^c . 
Técnica de agrupación de características exclusivas para LightGBM: 
Los datos de alta dimensión suelen ser muy escasos, lo que nos brinda la posibilidad de diseñar un enfoque casi sin pérdidas para reducir la cantidad de características. Específicamente, en un espacio de características dispersas, muchas características son mutuamente excluyentes, es decir, nunca toman valores distintos de cero simultáneamente. Las funciones exclusivas se pueden agrupar de forma segura en una sola función (llamada paquete de funciones exclusivas). Por lo tanto, la complejidad de la construcción de histogramas cambia de O(#data × #feature) a O(#data × #bundle) , mientras que #bundle<<#feature . Por lo tanto, la velocidad del marco de entrenamiento se mejora sin afectar la precisión. 
Algoritmo para la técnica de agrupación de características exclusivas: 

Input: numData: number of data
Input: F: One bundle of exclusive features
binRanges ? {0}, totalBin ? 0
for f in F do
    totalBin += f.numBin
    binRanges.append(totalBin)
newBin ? new Bin(numData)
for i = 1 to numData do
    newBin[i] ? 0
    for j = 1 to len(F) do

        if F[j].bin[i] != 0 then
            newBin[i] ? F[j].bin[i] + binRanges[j]
Output: newBin, binRanges

Arquitectura: 
LightGBM divide el árbol en hojas, a diferencia de otros algoritmos de impulso que hacen crecer el árbol en niveles. Elige la hoja con máxima pérdida delta para crecer. Dado que la hoja es fija, el algoritmo de hoja tiene una pérdida menor en comparación con el algoritmo de nivel. El crecimiento de los árboles por hojas podría aumentar la complejidad del modelo y provocar un sobreajuste en conjuntos de datos pequeños.
A continuación se muestra una representación esquemática del crecimiento de árboles sabios en hojas: 

Código: Implementación de Python del modelo LightGBM: 
el conjunto de datos utilizado para este ejemplo es Predicción del cáncer de mama. Haga clic aquí para obtener el conjunto de datos : Enlace al conjunto de datos. 

# installing LightGBM (Required in Jupyter Notebook and
# few other compilers once)
pip install lightgbm
 
# Importing Required Library
import pandas as pd
import lightgbm as lgb
 
# Similarly LGBMRegressor can also be imported for a regression model.
from lightgbm import LGBMClassifier
 
# Reading the train and test dataset
data = pd.read_csv("cancer_prediction.csv)
 
# Removing Columns not Required
data = data.drop(columns = ['Unnamed: 32'], axis = 1)
data = data.drop(columns = ['id'], axis = 1)
 
# Skipping Data Exploration
# Dummification of Diagnosis Column (1-Benign, 0-Malignant Cancer)
data['diagnosis']= pd.get_dummies(data['diagnosis'])
 
# Splitting Dataset in two parts
train = data[0:400]
test = data[400:568]
 
# Separating the independent and target variable on both data set
x_train = train.drop(columns =['diagnosis'], axis = 1)
y_train = train_data['diagnosis']
x_test = test_data.drop(columns =['diagnosis'], axis = 1)
y_test = test_data['diagnosis']
 
# Creating an object for model and fitting it on training data set
model = LGBMClassifier()
model.fit(x_train, y_train)
 
# Predicting the Target variable
pred = model.predict(x_test)
print(pred)
accuracy = model.score(x_test, y_test)
print(accuracy)

Output
Prediction array : 
[0 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1
 1 1 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1
 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0 1 0 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1
 1 0 1 0 1 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 0 0 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0]
Accuracy Score : 
0.9702380952380952

Ajuste de parámetros 
Algunos parámetros importantes y su uso se enumeran a continuación: 

1. max_ depth : Establece un límite en la profundidad del árbol. El valor predeterminado es 20. Es eficaz para controlar el ajuste.
2. categorical_feature: especifica la función categórica utilizada para el modelo de entrenamiento.
3. bagging_fraction : Especifica la fracción de datos a considerar para cada iteración.
4. num_iterations: Especifica el número de iteraciones a realizar. El valor predeterminado es 100.
5. num_leaves : Especifica el número de hojas en un árbol. Debe ser más pequeño que el cuadrado de max_ depth .
6. max_bin: especifica el número máximo de contenedores para depositar los valores de las características.
7. min_data_in_bin: especifica la cantidad mínima de datos en un contenedor.
8. task : Especifica la tarea que deseamos realizar, ya sea entrenar o predecir. La entrada predeterminada es tren . Otro valor posible para este parámetro es la predicción.
9. feature_fraction : Especifica la fracción de características a considerar en cada iteración. El valor predeterminado es «uno»